本质: 【广度优先遍历 】【贪心算法】应用于【有向图】的专有名词
应用场景:任务调度,课程安排
作用:
- 得到一个不唯一的【拓扑序】
- 检测【有向图】是否有环,使用数据【并查集】
使用:先找度为0的前驱节点,然后广度找点(把第一个前驱去掉,找其他没有前驱的节点)
题目举例:
你这个学期必须选修 numCourses 门课程,记为 0 到 numCourses - 1 。
在选修某些课程之前需要一些先修课程。 先修课程按数组 prerequisites 给出,其中 prerequisites[i] = [ai, bi] ,表示如果要学习课程 ai 则 必须 先学习课程 bi 。
-
例如,先修课程对
[0, 1]表示:想要学习课程0,你需要先完成课程1。
请你判断是否可能完成所有课程的学习?如果可以,返回 true ;否则,返回 false
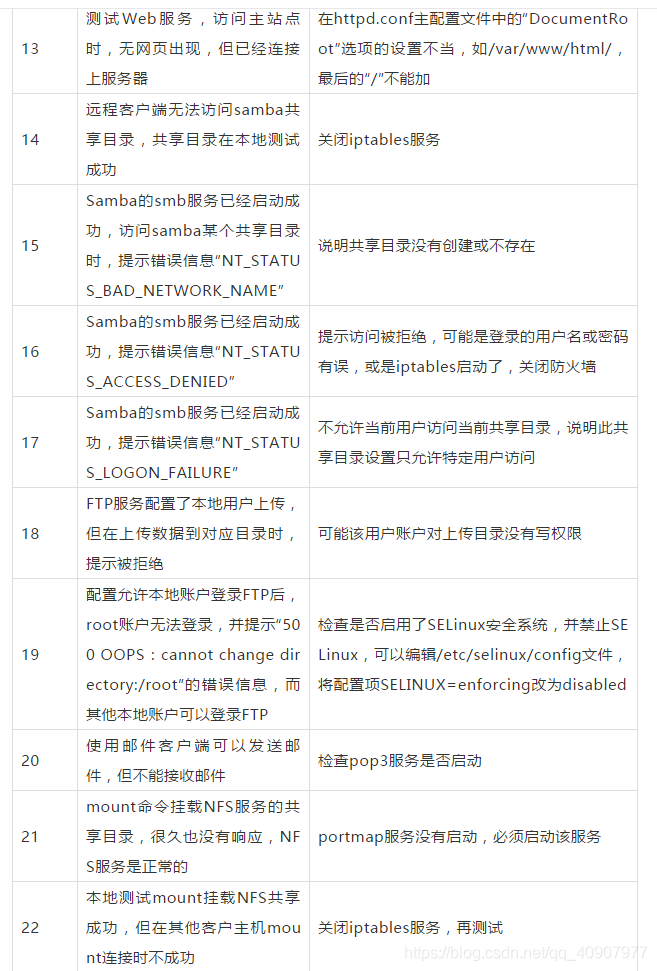
示例 1:
输入:numCourses = 2, prerequisites = [[1,0]] 输出:true 解释:总共有 2 门课程。学习课程 1 之前,你需要完成课程 0 。这是可能的
利用拓扑 根据依赖关系,构建邻接表ret(用来记录课程之间的关系)、入度数组ans(用来记录课程的依赖) 选取入度为 0 的数据,根据邻接表,减小依赖它的数据的入度。 找出入度变为 0 的数据,重复第 3 步(行)。 直至所有数据的入度为 0,得到排序
public boolean canFinish(int numCourses, int[][] prerequisites) {
int[] ans = new int[numCourses]; // 入度数组
List<List<Integer>> ret = new ArrayList<>(); // 邻接表
Queue<Integer> queue = new LinkedList<>();
for (int i = 0; i < numCourses; i++) {
ret.add(new ArrayList<>()); //初始化
}
for (int[] tmp:prerequisites) {
ans[tmp[0]]++; // 这门课需要依赖 入度++
ret.get(tmp[1]).add(tmp[0]); //邻接表 进行增加领接的数据
}
for (int i = 0; i < numCourses; i++) {
if(ans[i]==0){
queue.add(i); // 添加入度为0 - 即不需要进行依赖的课程
}
}
while (!queue.isEmpty()){
numCourses--; // --为后续确认是否成环判断/课程正常选完
int pre = queue.poll(); //临接数据
for (int cur:ret.get(pre)) {
if(--ans[cur] == 0){
queue.add(cur);
}
}
}
return numCourses==0;
}