目录
一、个人感受
二、题目与题解
题目一:卡码网 110. 字符串接龙
题目链接
题解:BFS+哈希
题目二:卡码网 105. 有向图的完全可达性
题目链接
题解:DFS
三、小结
一、个人感受
对于两大基本搜索:
深度优先搜索DFS遍历所有路径,每条路径都是一条路走到底,用于解决需要处理所有位置的情况;
广度优先搜索BFS遍历最近相邻路径(常用邻接图,邻接表实现),用于用于求得最短路径,最小次数等。
今天打卡题目个人感觉挺难,事实证明,图论这个章节还得多练。
二、题目与题解
题目一:卡码网 110. 字符串接龙
题目链接
110. 字符串接龙 (kamacoder.com)
题目描述
字典 strList 中从字符串 beginStr 和 endStr 的转换序列是一个按下述规格形成的序列:
1. 序列中第一个字符串是 beginStr。
2. 序列中最后一个字符串是 endStr。
3. 每次转换只能改变一个字符。
4. 转换过程中的中间字符串必须是字典 strList 中的字符串,且strList里的每个字符串只用使用一次。
给你两个字符串 beginStr 和 endStr 和一个字典 strList,找到从 beginStr 到 endStr 的最短转换序列中的字符串数目。如果不存在这样的转换序列,返回 0。
输入描述
第一行包含一个整数 N,表示字典 strList 中的字符串数量。 第二行包含两个字符串,用空格隔开,分别代表 beginStr 和 endStr。 后续 N 行,每行一个字符串,代表 strList 中的字符串。
输出描述
输出一个整数,代表从 beginStr 转换到 endStr 需要的最短转换序列中的字符串数量。如果不存在这样的转换序列,则输出 0。
输入示例
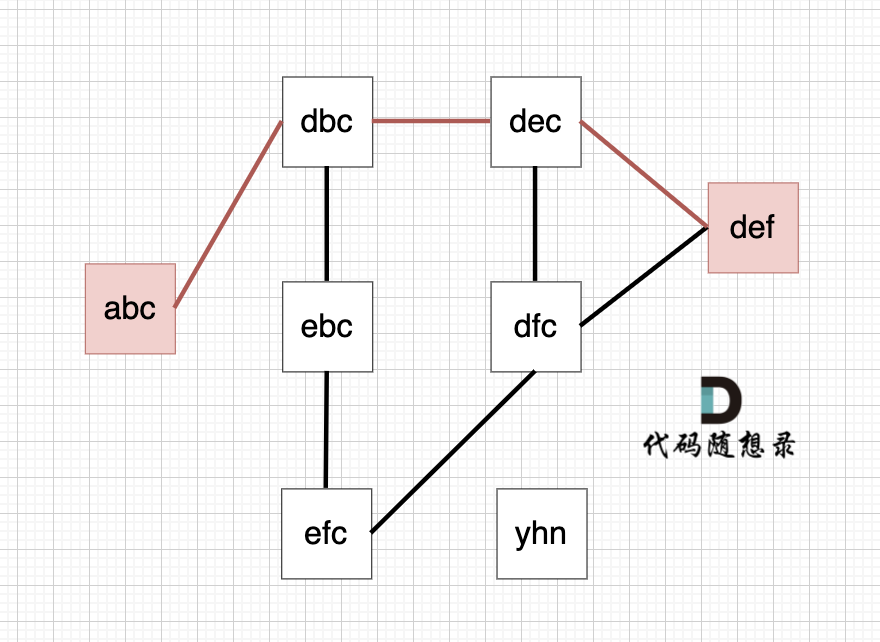
6 abc def efc dbc ebc dec dfc yhn输出示例
4提示信息
从 startStr 到 endStr,在 strList 中最短的路径为 abc -> dbc -> dec -> def,所以输出结果为 4,如图:
数据范围:
2 <= N <= 500
题解:BFS+哈希
这题的思路其实很简单,需要我们求得从 beginStr 转换到 endStr 需要的最短转换序列中的字符串数量,即是求得最短路径 -- 对于求得最短路径,优先选择 BFS。
关键:如何确定是否当前单词改掉一个字母可以得到目标单词?两层循环:尝试用26个字母去替代每个位置的字母,看是否满足。
广度优先搜索(BFS)的实现思路:
当队列不为空时,取出队头单词word并获取其路径长度path;
遍历单词word的每个字符位置i,尝试用字母表中的每个字母替换当前位置的字符,生成新的单词newWord;
如果newWord与目标单词endStr相同,则输出路径长度path +1并结束程序;
如果newWord在单词集合strSet中且未被访问过(不在visitMap中),则将newWord加入队列,并在visitMap中记录其路径长度为path + 1。
两个哈希:
使用一个unordered_set来存储所有合法的单词,方便后续快速查找;-- strSet
使用一个unordered_map来记录每个单词是否被访问过,以及到达该单词的路径长度。 -- visitMap
代码如下:
#include <bits/stdc++.h>
using namespace std;
int n;
string beginStr, endStr;
string str;
int main()
{
cin >> n; // 读取单词的数量
unordered_set<string> strSet; // 用于存储所有单词的集合
cin >> beginStr >> endStr; // 读取起始单词和目标单词
for (int i = 0; i < n; i++)
{
cin >> str; // 读取每个单词str并添加到集合strSet中
strSet.insert(str);
}
// visitMap用于记录每个单词是否被访问过,以及记录到达该单词的路径长度
unordered_map<string, int> visitMap; // <单词,路径长度> -- key为单词,value为路径长度
visitMap.insert(pair<string, int>(beginStr, 1)); // 初始化visitMap,记录起始单词的路径长度为1
queue<string> q; // 初始化队列q,用于实现BFS
q.push(beginStr); // 将起始单词加入队列
while (!q.empty())
{
string word = q.front(); // 获取队头的单词
q.pop(); // 出队列
int path = visitMap[word]; // 获取当前单词的路径长度
for (int i = 0; i < word.size(); i++) // 遍历当前单词的每个字符
{
string newWord = word; // 创建新单词,用于替换字符,初始化为word本身
for (int j = 0; j < 26; j++) // 尝试将当前字符替换为26个字母中的每一个 -- 注意i会遍历当前单词的所有字符,所以每个位置的情况都能考虑到(26个字符进行替换当前位置,找到与目标单词相同的情况)
{
newWord[i] = j + 'a'; // 替换字符 -- 数字0 - 25转化为字符串a - z
if (newWord == endStr) // 如果新单词与目标单词相同
{
cout << path + 1 << endl; // 输出路径长度:注意要+1
return 0; // 结束程序
}
if (strSet.find(newWord) != strSet.end() && visitMap.find(newWord) == visitMap.end()) // 如果新单词在集合中且未被访问过 -- BFS优先遍历周围相邻的一圈
{
// 记录新单词的访问信息,并将新单词加入队列
visitMap.insert(pair<string, int>(newWord, path + 1));
q.push(newWord);
}
}
}
}
cout << 0 << endl; // 如果队列为空仍未找到目标单词,则输出0
}
个人感觉代码实现比较复杂,需要理清楚每一步,尤其是两个哈希数组的实现,很容易出错。
题目二:卡码网 105. 有向图的完全可达性
题目链接
105. 有向图的完全可达性 (kamacoder.com)
题目描述
给定一个有向图,包含 N 个节点,节点编号分别为 1,2,...,N。现从 1 号节点开始,如果可以从 1 号节点的边可以到达任何节点,则输出 1,否则输出 -1。
输入描述
第一行包含两个正整数,表示节点数量 N 和边的数量 K。 后续 K 行,每行两个正整数 s 和 t,表示从 s 节点有一条边单向连接到 t 节点。
输出描述
如果可以从 1 号节点的边可以到达任何节点,则输出 1,否则输出 -1。
输入示例
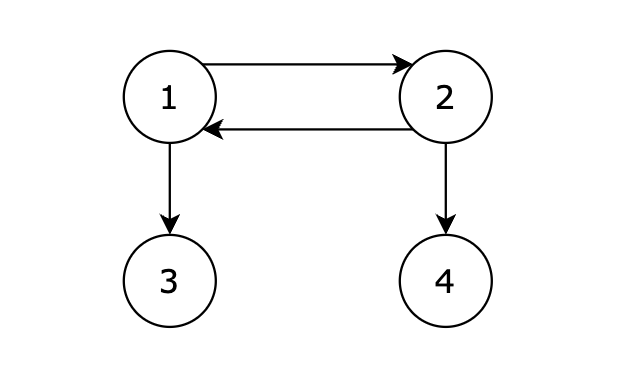
4 4 1 2 2 1 1 3 2 4输出示例
1提示信息
从 1 号节点可以到达任意节点,输出 1。
数据范围:
1 <= N <= 100;
1 <= K <= 2000。
题解:DFS
这题相对来说简单一点。
这题使用到了邻接图:用邻接表实现的图。个人感觉还是比较新颖,直接就能表示邻接的节点,就与之前的岛屿问题很像,区别就是:岛屿问题中,各个位置列于矩阵当中,相邻节点就是上下左右四个方向;而对于这种图的问题,相邻节点并非所谓的上下左右,我们需要使用邻接表实现。
理清楚这个后,其余思路同之前打卡的岛屿问题一致,这里不做过多解释。
代码如下:
#include <bits/stdc++.h>
using namespace std;
// graph: 邻接表表示的图:节点从1到n
// cur: 当前访问的节点
// visited: 记录节点是否被访问过
// neigbor:记录当前节点cur的相邻节点 -- 当前节点邻接表链接元素
void dfs(const vector<list<int>> &graph, int cur, vector<bool> &visited)
{
if (visited[cur]) // 如果当前节点已经被访问过,直接返回
return;
visited[cur] = true; // 标记当前节点为已访问
for (int neighbor : graph[cur]) // 遍历当前节点的邻接节点
{
dfs(graph, neighbor, visited); // 递归调用dfs,继续搜索邻接节点
}
}
int main()
{
int n, m, s, t;
cin >> n >> m; // 读取节点数n和边数m
vector<list<int>> graph(n + 1); // 创建一个大小为n+1的邻接表,其中list<int>:它存储了与节点i直接相连的所有其他节点的编号
while (m--) // 读取所有边的信息,并构建图
{
cin >> s >> t; // 读取一条边,s是起点,t是终点
graph[s].push_back(t); // 在邻接表中添加边s -> t -- 这里需注意:如果是无向图,还需要添加边t -> s,即graph[t].push_back(s);
}
vector<bool> visited(n + 1, false); // 创建一个大小为n+1的访问记录数组,初始都设置为未访问
dfs(graph, 1, visited); // 从节点1开始进行dfs
for (int i = 1; i <= n; i++) // 检查所有节点是否都被访问过
{
if (!visited[i]) // 如果有节点未被访问到
{
cout << -1 << endl; // 输出-1表示图不是连通的
return 0; // 结束程序
}
}
cout << 1 << endl; // 如果所有节点都被访问到,输出1表示图是连通的
return 0; // 结束程序
}
三、小结
今天的打卡到此也就结束了,后边有时间会对图论这一章节进行强化练习。