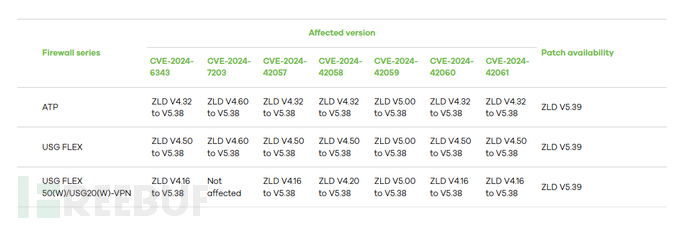
快速排序的复杂度

快排代码

package leetcode;

import java.util.Arrays;

public class QuickSort {
    public static void quickSort(int[] array, int low, int high) {
        if (low < high) {
            int pivotIndex = partition(array, low, high);
            quickSort(array, low, pivotIndex - 1);  // 递归排序左子数组
            quickSort(array, pivotIndex + 1, high); // 递归排序右子数组
        }
    }

    private static int partition(int[] array, int low, int high) {
        int pivot = array[high]; // 选择最后一个元素作为基准
       // high = high;
        while (low < high){
            while(low<high && array[low] <= pivot){
                low++;
            }
            array[high] = array[low];
            while(low<high && array[high] >= pivot){
                high--;
            }
            array[low] = array[high];
        }
        array[low] = pivot;

        return low;
    }

    public static void main(String[] args) {
        int[] arr = {4, 1};
        int n = arr.length;
        quickSort(arr, 0, n - 1);

        System.out.println("Sorted array: ");
        for (int value : arr) {
            System.out.print(value + " ");
        }
    }
}

对于每一次分区调整，上边的代码有点小问题，但是不影响正确性，

即代码

private static int partition(int[] array, int low, int high) {
        int pivot = array[high]; // 选择最后一个元素作为基准
       //也就说，一开始最右边的是相当于空着的
       //所以一开始要先找左边大于基准的，可以放到high空着的地方
        while (low < high){
            while(low<high && array[low] <= pivot){
                low++;
            }
            array[high] = array[low];//相当于现在low这个位置空着
            //所以需要再从右边找一个比基准小的
            // 但是每一次都会重复判断high
   
            while(low<high && array[high] >= pivot){
                high--;
            }
            array[low] = array[high];
        }
        array[low] = pivot;

        return low;
    }

array[high] = array[low];
while(low<high && array[high] >= pivot){
high–;
}
每一次都会重复判断high,因为上一行代码 array[high] = array[low];
所以array[high] >= pivot 一定成立，我就感觉多了一次判断。
array[high] >= pivot