
🤵♂️ 个人主页:@艾派森的个人主页
✍🏻作者简介:Python学习者
🐋 希望大家多多支持,我们一起进步!😄
如果文章对你有帮助的话,
欢迎评论 💬点赞👍🏻 收藏 📂加关注+
目录
问题的提出
TOPSIS法
基本概念
模型原理
基本步骤
①原始矩阵正向化
②正向化矩阵标准化
③计算得分并归一化
Python代码实现

问题的提出
生活中我们常常要进行评价,上一篇文章我们讲到了层次分析法,通过确定各指标的权重,来进行打分,但层次分析法决策层不能太多,而且构造判断矩阵相对主观。哪有没有别的方法呢?
研究问题:明星A在当选微博之星后想找个对象,但喜欢他的人太多,不知道怎么选,经过层层考察,留下三个候选人。
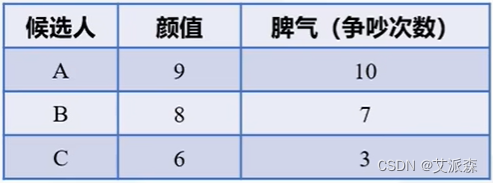
从表中可以看出,候选人A颜值最高,但是脾气不好,一个月吵10次架,平均三天一次;候选人B颜值略微低于A,但是脾气要稍微好点;候选人C颜值虽然相比前两位较差,但是脾气是最好最稳定的。
理想情况下:
- 最好的对象应该是颜值9,脾气3
- 最差的对象应该是颜值6,脾气10
思考:那怎么衡量A、B、C和最好、最差的距离呢?
- 把(9,3),(6,10)作为二维平面的一个点
- 距离最好点最近或者距离最差点最远的的就是综合条件最好的
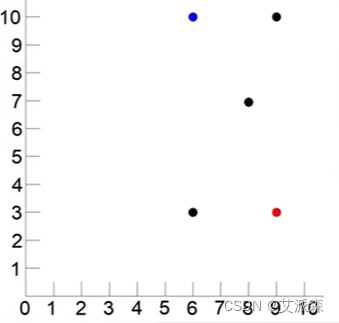
在上图中红色的点就是最好的对象,蓝色的点就是最差的对象,三个黑点代表三位候选人,可以看出(6,3)距离红色点最近,距离蓝色点最远,可以说是综合条件最好的。
TOPSIS法
基本概念
C.L.Hwang和K.Yoon于1981年首次提出 TOPSIS (Technique for 0rder Preference bySimilarity to an Ideal Solution),可翻译为逼近理想解排序法,国内常简称为优劣解距离法,。
TOPSIS法是一种常用的综合评价方法,能充分利用原始数据的信息,其结果能精确地反映各评价方案之间的差距。TOPSIS法引入了两个基本概念:
- 理想解:设想的最优的解(方案),它的各个属性值都达到各备选方案中的最好的值;
- 负理想解:设想的最劣的解(方案),它的各个属性值都达到各备选方案中的最坏的值。
方案排序的规则是把各备选方案与理想解和负理想解做比较,若其中有一个方案最接近理想解,而同时又远离负理想解,则该方案是备选方案中最好的方案。TOPSIS通过最接近理想解且最远离负理想解来确定最优选择。
模型原理
TOPSIS法是一种理想目标相似性的顺序选优技术,在多目标决策分析中是一种非常有效的方法它通过归一化后(去量纲化)的数据规范化矩阵,找出多个目标中最优目标和最劣目标(分别用理归想一解化和反理想解表示),分别计算各评价目标与理想解和反理想解的距离,获得各目标与理想解的贴近度,按理想解贴近度的大小排序,以此作为评价目标优劣的依据。贴近度取值在0~1之间,该值愈接近1,表示相应的评价目标越接近最优水平;反之,该值愈接近0,表示评价目标越接近最劣水平。
基本步骤
1.将原始矩阵正向化:将原始矩阵正向化,就是要将所有的指标类型统一转化为极大型指标,因为有些指标并不是越大越好,它是越小越好,比如前面我们提到的吵架的次数。
2.正向矩阵标准化:标准化的方法有很多种,其主要目的就是去除量纲的影响,保证不同评价指标在同一数量级,且数据大小排序不变。
3.计算得分并归一化
其中
为得分,
为评价对象与最大值的距离,
为评价对象与最小值的距离。
我们回到给明星A找对象这件事上
明星A考虑了一下觉得光靠颜值和脾气可能考虑的还不够全面,就又加上了身高和体重两个指标,而且他认为身高165是最好,体重在90-100斤是最好。

①原始矩阵正向化
在原始矩阵正向化之前,我们需要先知道都有哪些类型的指标,指标一共有如下四种:

将原始矩阵正向化,就是要将所有的指标类型统一转化为极大型指标。四种指标转化公式如下:

在了解了指标正向化的公式后,我们将原始指标进行正向化:

②正向化矩阵标准化
标准化的目的是消除不同指标量纲的影响。
假设有n个要评价的对象,m个评价指标(已正向化)构成的正向化矩阵如下:
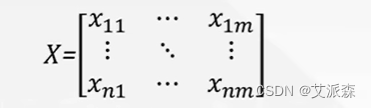
那么,对其标准化的矩阵记为Z,Z中的每一个元素:

标准化后,还需给不同指标加上权重,采用的权重确定方法有层次分析法、熵权法、Delphi法
对数最小二乘法等。在这里认为各个指标的权重相同。将正向化矩阵标准化后如下:
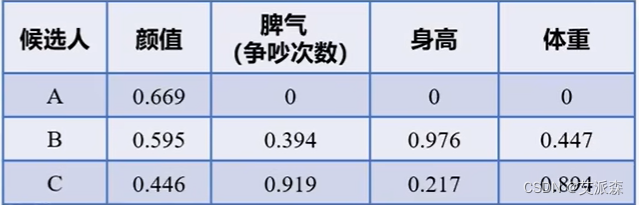
③计算得分并归一化
上一步得到标准化矩阵Z

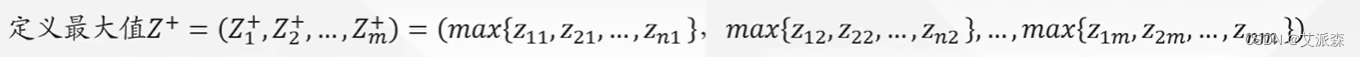
![]()


那么,我们可以计算得出第i(i= 1,2,…,n)个评价对象未归一化的得分:
很明显0≤≤1,且
越大
越小,即越接近最大值。
我们可以将得分归一化并换成百分制:
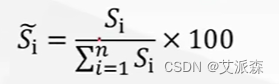
首先对于前面的标准化矩阵计算得分:
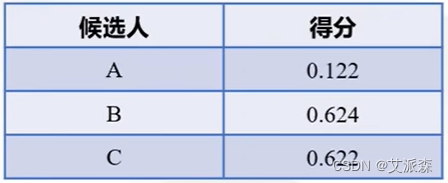
然后再进行归一化并换算为百分制:
最后可以看出候选人B以微弱的优势胜出,所有最终明星A选择了候选人B作为对象。
Python代码实现
实现方法一:手动输入数据
import numpy as np #导入numpy库,用于选行科学计算
# 从用户输入中接收参评效目和指标数目,并将输入的字符事转换为数值
n = int(input("请输入参评数目:")) # 接收参评数目
m = int(input("请输入指标数目:")) # 接收指标数目
# 接收用户输入的类型矩阵,该矩阵指示了每个指标的类型(极大型、极小型等)
kind = input("请输入类型矩阵(1:极大型,2:极小型,3:中间型,4:区间型):").split(" ") # 将输入的字符串按空格分割,形成列表
# 接收用户输入的矩阵并转换为numpy数组
print("请输入矩阵:")
A = np.zeros(shape=(n,m)) #初 始化一个n行m列的全零矩阵A
for i in range(n):
A[i] = input().split(" ") # 接收每行输入的数据
A[i] = list(map(float, A[i])) # 将接收到的字符串列表转换为浮点数列表
print("输入矩阵为:\n{}".format(A)) # 打印输入的矩阵A
# 极小型指标转化为极大型指标的函数
def minTomax(maxx,x):
x = list(x) # 将输入的指标效据转换为列表
ans = [[(maxx-e)] for e in x] # 计算最大值与每个指标值的差,并将其放入新列表中
return np.array(ans) # 将列表转换为numpy数组并返回
# 中间型指标转化为极大型指标的函数
def midTomax(bestx,x):
x = list(x) # 将输入的指标效据转换为列表
h = [abs(e-bestx)for e in x] # 计算每个指标值与最优值之间的绝对差
M = max(h) # 找到最大的差值
if M == 0:
M = 1 # 防止最大差值为0的情况
ans = [[(1-e/M)]for e in h] # 计算每个差值占最大差值的比例,并从1中减去,得到新指标值
return np.array(ans) # 返回处理后的numpy数组
# 区间型指标转化为极大型指标的函数
def regTomax(lowx,highx,x):
x = list(x) # 将输入的指标效据转换为列表
M = max(lowx-min(x),max(x)-highx) # 计算指标值超出区间的最大距高
if M == 0:
M = 1 # 防止最大距离为0的情况
ans = []
for i in range(len(x)):
if x[i]<lowx:
ans.append([(1-(lowx-x[i])/M)]) # 如果指标值小于下限,则计算其与下限的距离比例
elif x[i]>highx:
ans.append([(1-(x[i]-highx)/M)]) # 如果指标值大于上限,则计算其与上限的距离比例
else:
ans.append([1]) # 如果指标值在区间内,则直接职为1
return np.array(ans) #返回处理后的numpy数组
# 统一指标类型,将所有指标转化为极大型指标
X = np.zeros(shape=(n,1))
for i in range(m):
if kind[i]=="1": # 如果当前指标为极大型,则直接使用原值
v= np.array(A[:,i])
elif kind[i]=="2": # 如果当前指标为极小型,调用minTomax函数转换
maxA = max(A[:,i])
v = minTomax(maxA,A[:,i])
elif kind[i]=="3": # 如果当前指标为中间型,调用midTomax函数转换
bestA = float(eval(input("【类型三】请输入最优值:")))
v = midTomax(bestA,A[:,i])
elif kind[i]=="4": #如果当前指标为区间型,调用regTomax的数转换
lowA = float(eval(input("【类型四】请输入区间[a,b]值a:")))
highA = float(eval(input("【类型四】请输入区间[a,b]值b:")))
v = regTomax(lowA, highA, A[:,i])
if i==0:
X = v.reshape(-1,1) # 如果是第一个指标,直接替换X数组
else:
X= np.hstack([X,v.reshape(-1,1)]) # 如果不是第一个指标,则将新指标列拼接到X敬组上
print("统一指标后矩阵为:\n{}".format(X)) # 打印处理后的矩阵X
# 对统一指标后的矩阵X进行标准化处理
X = X.astype(float)
for j in range(m):
X[:,j] = X[:,j]/np.sqrt(sum(X[:,j]**2)) # 对每一列数据进行归一化处理,即除以该列的欧几里得范效
print("标准化矩阵为:\n{}".format(X)) # 打印标准化后的矩阵X
# 最大值最小值距离的计算
x_max = np.max(X,axis=0) # 计算标准化矩阵每列的最大值
x_min= np.min(X,axis=0) # 计算标准化矩阵每列的最小值
d_z = np.sqrt(np.sum(np.square((X- np.tile(x_max,(n,1)))),axis=1)) # 计算每个参评对象与最优情况的距离d+
d_f = np.sqrt(np.sum(np.square((X- np.tile(x_min,(n,1)))),axis=1)) # 计算每个参评对象与最劣情况的距离d-
print('每个指标的最大值:',x_max)
print('每个指标的最小值:',x_min)
print('d+向量:',d_z)
print('d-向量:',d_f)
# 计算每个参评对象的得分排名
s = d_f/(d_z+d_f) # 根据d+和d-计算得分s,其中s接近于1则表示较优,接近于0则表示较劣
Score = 100*s/sum(s) # 将得分s转换为百分制,便于比较
for i in range(len(Score)):
print(f"第{i+1}个标准化后百分制得分为:{Score[i]}") # 打印每个参评对象的得分运行上面代码后,我们以前面的问题为例进行输入数据(明星A认为身高165是最好,体重在90-100斤是最好)。其中,参评数目就是三个候选人;指标数目就是颜值、吵架次数、身高、体重四个指标;类型矩阵颜值是极大型,吵架次数是极小型,身高是中间型,体重是区间型,所以对应输入为1 2 3 4 用空格隔开;在输入矩阵的时候,每行分别输入三个候选者的四个指标,用空格隔开,输入完一个候选者的指标后按回车键开启下一行;因为身高是类型三中间型,所有我们需要输入165;体重是区间型,依次输入90和100即可。

在输入上面的数据后,运行结果如下:
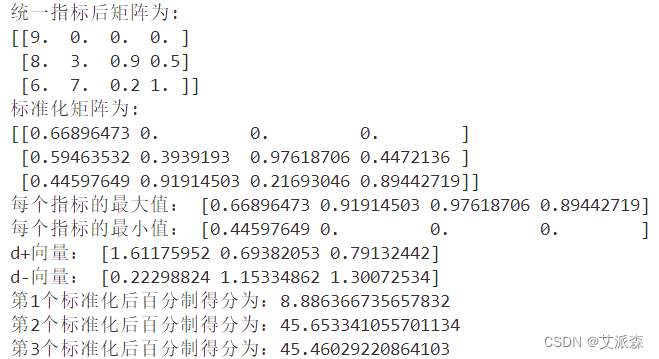
从结果可以看出,第二个参评对象的得分最高为45.65,也就对应着候选人B。
实现方法二:导入外部文件数据
import numpy as np # 导入numpy包并将其命名为np
# 定义正向化的函数
def positivization(x,type,i):
# x:需要正向化处理的指标对应的原始向量
# type:指标类型(1:极小型,2:中间型,3:区间型)
# i:正在处理的是原始矩阵的哪一列
if type == 1: #极小型
print("第",i,"列是极小型,正向化中...")
posit_x = x.max(0)-x
print("第",i,"列极小型处理完成!")
print("--------------------------分隔--------------------------")
return posit_x
elif type == 2: #中间型
print("第",i,"列是中间型")
best = int(input("请输入最佳值:"))
m = (abs(x-best)).max()
posit_x = 1-abs(x-best)/m
print("第",i,"列中间型处理完成!")
print("--------------------------分隔--------------------------")
return posit_x
elif type == 3: #区间型
print("第",i,"列是区间型")
a,b = [int(l) for l in input("按顺序输入最佳区间的左右界,并用逗号隔开:").split(",")]
m = (np.append(a-x.min(),x.max()-b)).max()
x_row = x.shape[0] #获取x的行数
posit_x = np.zeros((x_row,1),dtype=float)
for r in range(x_row):
if x[r] < a:
posit_x[r] = 1-(a-x[r])/m
elif x[r] > b:
posit_x[r] = 1-(x[r]-b)/m
else:
posit_x[r] = 1
print("第",i,"列区间型处理完成!")
print("--------------------------分隔--------------------------")
return posit_x.reshape(x_row)
## 第一步:从外部导入数据
# 推荐使用csv格式文件
x_mat = np.loadtxt('data.csv', encoding='UTF-8-sig', delimiter=',',skiprows=1)
## 第二步:判断是否需要正向化
n, m = x_mat.shape
print("共有", n, "个评价对象", m, "个评价指标")
judge = int(input("指标是否需要正向化处理(需要请输入1,不需要则输入0):"))
if judge == 1:
position = np.array([int(i) for i in input("请输入需要正向化处理的指标所在的列(例如第1、3、4列需要处理,则输入1,3,4):").split(',')])
position = position-1
typ = np.array([int(j) for j in input("请按照顺序输入这些列的指标类型(1:极小型,2:中间型,3:区间型)格式同上:").split(',')])
for k in range(position.shape[0]):
x_mat[:, position[k]] = positivization(x_mat[:, position[k]], typ[k], position[k])
print("正向化后的矩阵:\n", x_mat)
## 第三步:对正向化后的矩阵进行标准化
tep_x1 = (x_mat * x_mat).sum(axis=0) # 每个元素平方后按列相加
tep_x2 = np.tile(tep_x1, (n, 1)) # 将矩阵tep_x1平铺n行
Z = x_mat / ((tep_x2) ** 0.5) # Z为标准化矩阵
print("标准化后的矩阵为:\n", Z)
## 第四步:计算与最大值和最小值的距离,并算出得分
tep_max = Z.max(0) # 得到Z中每列的最大值
tep_min = Z.min(0) # 每列的最小值
tep_a = Z - np.tile(tep_max, (n, 1)) # 将tep_max向下平铺n行,并与Z中的每个对应元素做差
tep_i = Z - np.tile(tep_min, (n, 1)) # 将tep_max向下平铺n行,并与Z中的每个对应元素做差
D_P = ((tep_a ** 2).sum(axis=1)) ** 0.5 # D+与最大值的距离向量
D_N = ((tep_i ** 2).sum(axis=1)) ** 0.5
S = D_N / (D_P + D_N) # 未归一化的得分
std_S = S / S.sum(axis=0)
sorted_S = np.sort(std_S, axis=0)
print('标准化后的得分:',std_S) # 打印标准化后的得分
## std_S.to_csv(std_S.csv) 结果输出到std_S.csv文件
在运行上面代码之前,需要准备csv格式的数据文件,同时需要注意文件路径,本实验代码与数据文件在同一目录下,本实验csv数据文件如下(还是以前面的问题为例):
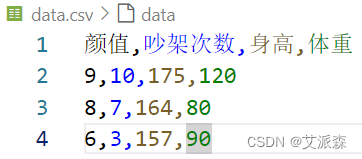
代码运行后,系统会根据数据文件打印有多少个评价对象和评价指标,接着输入0或1表示是否需要正向化处理;然后输入需要正向化处理的列,这里吵架次数、身高、体重需要处理,对应着第2,3,4列,用英文逗号隔开;指标类型的话按照要求输入,1,2,3;输入中间型的最佳值165;输入区间型的左右界,90,100。

最后输入完,运行结果如下:

可以看出结果与方法一得出的一致。
实现方法三:增加权重
前面两个方法中,我们是没有加上权重的,即默认权重都一样。那么假如现在我们在前面的问题中,分别给颜值、炒架次数、身高、体重赋上0.4、0.3、0.2、0.1的权重。那么我们就需要在正向矩阵标准化之后乘以对应的权重,代码如下:
import numpy as np #导入numpy库,用于选行科学计算
# 从用户输入中接收参评效目和指标数目,并将输入的字符事转换为数值
n = int(input("请输入参评数目:")) # 接收参评数目
m = int(input("请输入指标数目:")) # 接收指标数目
# 接收用户输入的类型矩阵,该矩阵指示了每个指标的类型(极大型、极小型等)
kind = input("请输入类型矩阵(1:极大型,2:极小型,3:中间型,4:区间型):").split(" ") # 将输入的字符串按空格分割,形成列表
# 接收用户输入的矩阵并转换为numpy数组
print("请输入矩阵:")
A = np.zeros(shape=(n,m)) #初 始化一个n行m列的全零矩阵A
for i in range(n):
A[i] = input().split(" ") # 接收每行输入的数据
A[i] = list(map(float, A[i])) # 将接收到的字符串列表转换为浮点数列表
print("输入矩阵为:\n{}".format(A)) # 打印输入的矩阵A
# 极小型指标转化为极大型指标的函数
def minTomax(maxx,x):
x = list(x) # 将输入的指标效据转换为列表
ans = [[(maxx-e)] for e in x] # 计算最大值与每个指标值的差,并将其放入新列表中
return np.array(ans) # 将列表转换为numpy数组并返回
# 中间型指标转化为极大型指标的函数
def midTomax(bestx,x):
x = list(x) # 将输入的指标效据转换为列表
h = [abs(e-bestx)for e in x] # 计算每个指标值与最优值之间的绝对差
M = max(h) # 找到最大的差值
if M == 0:
M = 1 # 防止最大差值为0的情况
ans = [[(1-e/M)]for e in h] # 计算每个差值占最大差值的比例,并从1中减去,得到新指标值
return np.array(ans) # 返回处理后的numpy数组
# 区间型指标转化为极大型指标的函数
def regTomax(lowx,highx,x):
x = list(x) # 将输入的指标效据转换为列表
M = max(lowx-min(x),max(x)-highx) # 计算指标值超出区间的最大距高
if M == 0:
M = 1 # 防止最大距离为0的情况
ans = []
for i in range(len(x)):
if x[i]<lowx:
ans.append([(1-(lowx-x[i])/M)]) # 如果指标值小于下限,则计算其与下限的距离比例
elif x[i]>highx:
ans.append([(1-(x[i]-highx)/M)]) # 如果指标值大于上限,则计算其与上限的距离比例
else:
ans.append([1]) # 如果指标值在区间内,则直接职为1
return np.array(ans) #返回处理后的numpy数组
# 统一指标类型,将所有指标转化为极大型指标
X = np.zeros(shape=(n,1))
for i in range(m):
if kind[i]=="1": # 如果当前指标为极大型,则直接使用原值
v= np.array(A[:,i])
elif kind[i]=="2": # 如果当前指标为极小型,调用minTomax函数转换
maxA = max(A[:,i])
v = minTomax(maxA,A[:,i])
elif kind[i]=="3": # 如果当前指标为中间型,调用midTomax函数转换
bestA = float(eval(input("【类型三】请输入最优值:")))
v = midTomax(bestA,A[:,i])
elif kind[i]=="4": #如果当前指标为区间型,调用regTomax的数转换
lowA = float(eval(input("【类型四】请输入区间[a,b]值a:")))
highA = float(eval(input("【类型四】请输入区间[a,b]值b:")))
v = regTomax(lowA, highA, A[:,i])
if i==0:
X = v.reshape(-1,1) # 如果是第一个指标,直接替换X数组
else:
X= np.hstack([X,v.reshape(-1,1)]) # 如果不是第一个指标,则将新指标列拼接到X敬组上
print("统一指标后矩阵为:\n{}".format(X)) # 打印处理后的矩阵X
# 对统一指标后的矩阵X进行标准化处理
X = X.astype(float)
for j in range(m):
X[:,j] = X[:,j]/np.sqrt(sum(X[:,j]**2)) # 对每一列数据进行归一化处理,即除以该列的欧几里得范效
print("标准化矩阵为:\n{}".format(X)) # 打印标准化后的矩阵X
# 给标准化后的矩阵加上权重
weights = [0.4,0.3,0.2,0.1]
temp_list = []
for i,j in zip(X.T,weights):
temp_list.append(i*j)
import pandas as pd
new_X = pd.DataFrame(data=temp_list).T.to_numpy()
print("加上权重后的标准化矩阵为:\n{}".format(X)) # 打印加上权重后的标准化后的矩阵new_X
# 最大值最小值距离的计算
x_max = np.max(new_X,axis=0) # 计算标准化矩阵每列的最大值
x_min= np.min(new_X,axis=0) # 计算标准化矩阵每列的最小值
d_z = np.sqrt(np.sum(np.square((new_X- np.tile(x_max,(n,1)))),axis=1)) # 计算每个参评对象与最优情况的距离d+
d_f = np.sqrt(np.sum(np.square((new_X- np.tile(x_min,(n,1)))),axis=1)) # 计算每个参评对象与最劣情况的距离d-
print('每个指标的最大值:',x_max)
print('每个指标的最小值:',x_min)
print('d+向量:',d_z)
print('d-向量:',d_f)
# 计算每个参评对象的得分排名
s = d_f/(d_z+d_f) # 根据d+和d-计算得分s,其中s接近于1则表示较优,接近于0则表示较劣
Score = 100*s/sum(s) # 将得分s转换为百分制,便于比较
for i in range(len(Score)):
print(f"第{i+1}个标准化后百分制得分为:{Score[i]}") # 打印每个参评对象的得分代码运行结果如下:

从结果可以看出,如果给指标加上权重,最后的得分明显会不一样,此时候选人C得分最高。
实战案例
某一教育评估机构对5个研究生院进行评估。该机构选取了4个评价指标:人均专著、生师比、科研经费、逾期毕业率。

解释:人均专著和科研经费是效益性指标,逾期毕业率是成本型指标,生师比是区间型指标,最优范围是[5,6]。4个指标权重采用专家打分的结果,分别为0.2,0.3,0.4和0.1。
代码如下:
import numpy as np # 导入numpy包并将其命名为np
# 定义正向化的函数
def positivization(x,type,i):
# x:需要正向化处理的指标对应的原始向量
# type:指标类型(1:极小型,2:中间型,3:区间型)
# i:正在处理的是原始矩阵的哪一列
if type == 1: #极小型
print("第",i,"列是极小型,正向化中...")
posit_x = x.max(0)-x
print("第",i,"列极小型处理完成!")
print("--------------------------分隔--------------------------")
return posit_x
elif type == 2: #中间型
print("第",i,"列是中间型")
best = int(input("请输入最佳值:"))
m = (abs(x-best)).max()
posit_x = 1-abs(x-best)/m
print("第",i,"列中间型处理完成!")
print("--------------------------分隔--------------------------")
return posit_x
elif type == 3: #区间型
print("第",i,"列是区间型")
a,b = [int(l) for l in input("按顺序输入最佳区间的左右界,并用逗号隔开:").split(",")]
m = (np.append(a-x.min(),x.max()-b)).max()
x_row = x.shape[0] #获取x的行数
posit_x = np.zeros((x_row,1),dtype=float)
for r in range(x_row):
if x[r] < a:
posit_x[r] = 1-(a-x[r])/m
elif x[r] > b:
posit_x[r] = 1-(x[r]-b)/m
else:
posit_x[r] = 1
print("第",i,"列区间型处理完成!")
print("--------------------------分隔--------------------------")
return posit_x.reshape(x_row)
## 第一步:从外部导入数据
# 推荐使用csv格式文件
x_mat = np.loadtxt('TOPSIS案例.csv', encoding='UTF-8-sig', delimiter=',',skiprows=1,usecols=[1,2,3,4])
## 第二步:判断是否需要正向化
n, m = x_mat.shape
print("共有", n, "个评价对象", m, "个评价指标")
judge = int(input("指标是否需要正向化处理(需要请输入1,不需要则输入0):"))
if judge == 1:
position = np.array([int(i) for i in input("请输入需要正向化处理的指标所在的列(例如第1、3、4列需要处理,则输入1,3,4):").split(',')])
position = position-1
typ = np.array([int(j) for j in input("请按照顺序输入这些列的指标类型(1:极小型,2:中间型,3:区间型)格式同上:").split(',')])
for k in range(position.shape[0]):
x_mat[:, position[k]] = positivization(x_mat[:, position[k]], typ[k], position[k])
print("正向化后的矩阵:\n", x_mat)
## 第三步:对正向化后的矩阵进行标准化
tep_x1 = (x_mat * x_mat).sum(axis=0) # 每个元素平方后按列相加
tep_x2 = np.tile(tep_x1, (n, 1)) # 将矩阵tep_x1平铺n行
Z = x_mat / ((tep_x2) ** 0.5) # Z为标准化矩阵
print("标准化后的矩阵为:\n", Z)
# 给标准化后的矩阵加上权重
weights = [0.2,0.3,0.4,0.1]
temp_list = []
for i,j in zip(Z.T,weights):
temp_list.append(i*j)
import pandas as pd
new_Z = pd.DataFrame(data=temp_list).T.to_numpy()
print("加上权重后的标准化矩阵为:\n{}".format(new_Z)) # 打印加上权重后的标准化后的矩阵new_X
## 第四步:计算与最大值和最小值的距离,并算出得分
tep_max = new_Z.max(0) # 得到Z中每列的最大值
tep_min = new_Z.min(0) # 每列的最小值
tep_a = new_Z - np.tile(tep_max, (n, 1)) # 将tep_max向下平铺n行,并与Z中的每个对应元素做差
tep_i = new_Z - np.tile(tep_min, (n, 1)) # 将tep_max向下平铺n行,并与Z中的每个对应元素做差
D_P = ((tep_a ** 2).sum(axis=1)) ** 0.5 # D+与最大值的距离向量
D_N = ((tep_i ** 2).sum(axis=1)) ** 0.5
S = D_N / (D_P + D_N) # 未归一化的得分
std_S = S / S.sum(axis=0)
sorted_S = np.sort(std_S, axis=0)
print('标准化后的得分:',[x*100 for x in std_S]) # 打印标准化后的得分
在导入数据文件的时候,我们需要选取指标所在列,故需要再np.loadtxt()函数中加上参数usecols=[1,2,3,4],注意在Python中索引是从0开始的,0列对应的就是研究生院。同时我们还需要再代码中添加权重weights = [0.2,0.3,0.4,0.1]。
代码运行结果:
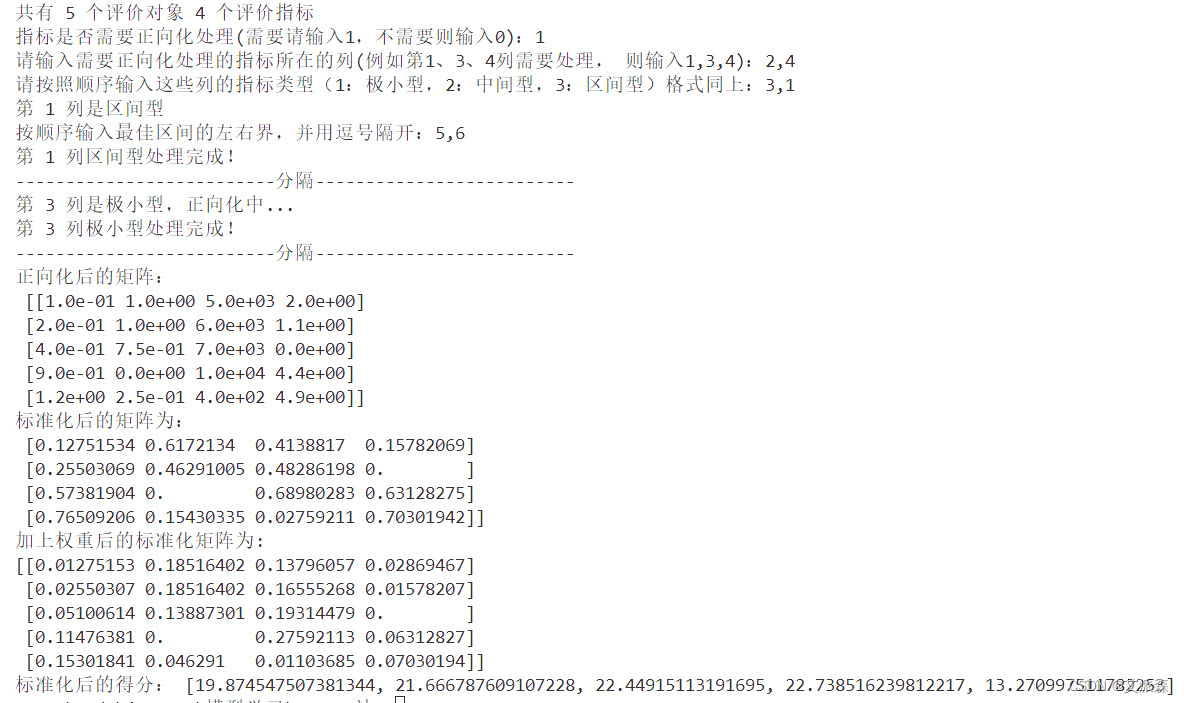
从结果可以看出4号研究生院以得分22.73微弱的优势胜出。
资料获取,更多粉丝福利,关注下方公众号获取




















