引言
通过前面的文章,我们已经掌握了Python中常用的装饰器的使用技巧,这篇文章中,我们通过一个装饰器的实战案例,来进一步加深对装饰器的适用场景的理解。
本文的主要内容有:
1、递归函数
2、递归实现斐波那契数列的计算
3、递归函数的性能优化
递归函数
相信稍微接触过编程的同学,一定都听过“递归”。所谓“递归函数(Recursive Function)”是一种在定义过程中调用自身的函数。递归是一种很自然的解决问题的有效编程技术,特别适用于那些大规模的计算问题可以分解为相同问题,只是规模更小的子问题的情况。
一个递归函数,必须包含两个组成部分:
1、基准情况(Base Case):这是递归的终止条件,确保递归不会无限进行。当基准条件满足时,函数返回一个具体的值,而不再是函数的递归调用。
2、递归情况(Recursive Case):这是函数调用自身的情况,通常是将问题规模不断减小的情况下进行递归调用。
所以,一个极简的递归函数的写法大概如下:
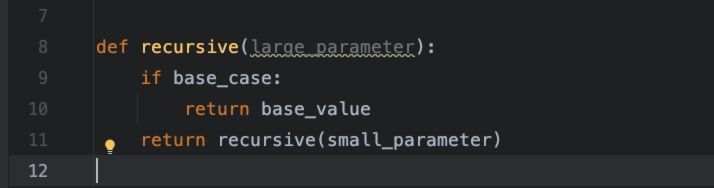
递归函数通常有3个特性,需要注意:
1、简洁性:递归函数的代码实现往往会比循环、迭代的实现更加简洁,而且可读性更高,特别是对于树结构和图结构等复杂的数据结构。
2、分而治之:递归思想,天然适用于这种分而治之的策略,大事化小,问题不变,规模不断缩小。
3、堆栈使用:由于每次递归调用都会在堆栈中创建一个新的函数调用,该函数使用的栈的深度会不断增加,因此,深度过大的递归可能导致堆栈溢出(Stack Overflow)。
为了避免过深的堆栈,导致内存溢出等问题,Python中会有一个默认的递归限制,我们可以通过sys模块获取递归调用栈的最大深度。
import sys
print(f'递归调用的最大栈深:{sys.getrecursionlimit()}')执行结果:

可以看到,在笔者的运行环境中,当前的最大栈深默认为1000,也就意味着,超过1000的会被自动终止。
我们试着写一个“忘记”写基准情况的无限递归,来验证下栈深:
stack_depth = 0
def infinite_recursive():
global stack_depth
stack_depth += 1
print(f'当前栈深:{stack_depth}')
return infinite_recursive()
infinite_recursive()
执行结果:
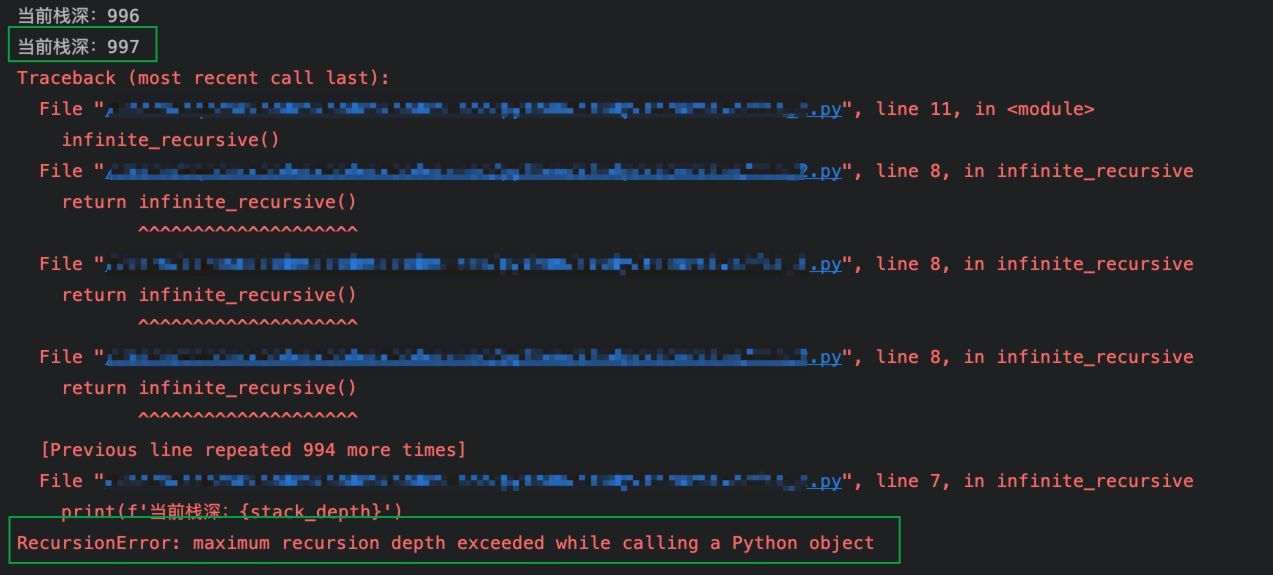
可以看到,实际执行时,由于其他代码的执行也会占用,实际的栈深会略小于栈深的默认限制。
递归实现斐波那契数列的计算
已经了解了递归函数的用法,我们通过递归函数来实现一个斐波那契数列的计算的需求。
简单介绍一下所谓的斐波那契数列:
斐波那契数列(Fibonacci Sequence)是一个在数学和自然界中广泛存在的有趣的数列,以意大利数学家斐波那契的名字命名。满足如下规律:
1、数列的前两个数字通常定义为0和1(有时也使用两个1作为开始)。
2、从第三个数字开始,每个数都是前两个数字之和。
斐波那契数列不仅在数学中有各种应用,在自然现象中也有,比如:植物的叶序、花瓣的排列等,此外,这个数列还与黄金比例(1.618)有着密切的关系——当数列趋于无穷时,相邻两个数的比值将接近于黄金比例。
我们通过递归函数来实现求斐波那契数列中任意位置的数字:
def fibonacci(n):
if n == 1:
return 0
if n == 2:
return 1
return fibonacci(n - 1) + fibonacci(n - 2)
if __name__ == '__main__':
for i in range(1, 30):
print(fibonacci(i), end=' ')
运行结果:

递归函数的性能优化
递归相对于迭代,代码会更加简洁、可读。但是,很多事情都是有利有弊的。递归算法的最大问题在于性能的开销,尤其当递归的深度较大时,或者递归算法本身存在的大量的重复计算。
我们上面的斐波那契数列的递归函数就是存在大量的重复计算,导致参数稍微大点,就会要大量的等待时间。
比如:
import time
def fibonacci(n):
if n == 1:
return 0
if n == 2:
return 1
return fibonacci(n - 1) + fibonacci(n - 2)
if __name__ == '__main__':
for i in range(30, 40):
start = time.time()
res = fibonacci(i)
end = time.time()
print(f"Fib({i}) = {res} 耗时:{round(end -start, 2)} 秒")
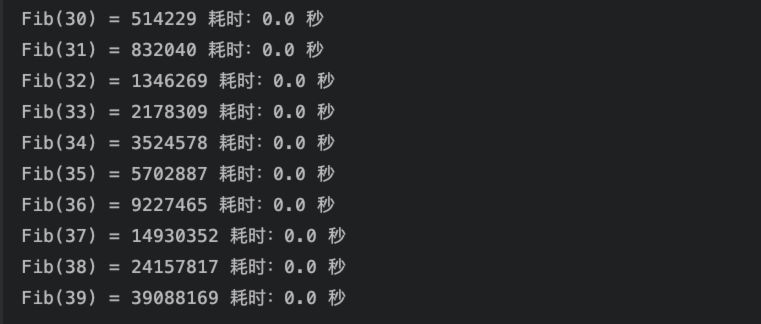
执行结果:
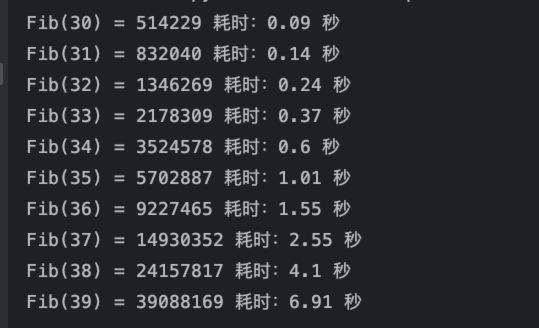
从计算结果可以看到,超过30时,就已经有很明显的延迟了。
其实,对递归函数的性能优化,本质上都是尽量消除重复计算,可以通过转换为迭代、使用缓存等。
我们首先看常规的优化策略:
优化方法1:
import time
def fibonacci(n):
if n == 1:
return 0
if n == 2:
return 1
fib = [0] * (n + 1)
fib[1] = 0
fib[2] = 1
for i in range(3, n + 1):
fib[i] = fib[i - 1] + fib[i - 2]
return fib[n]
if __name__ == '__main__':
for i in range(30, 40):
start = time.time()
res = fibonacci(i)
end = time.time()
print(f"Fib({i}) = {res} 耗时:{round(end - start, 4)} 秒")
先看效果:
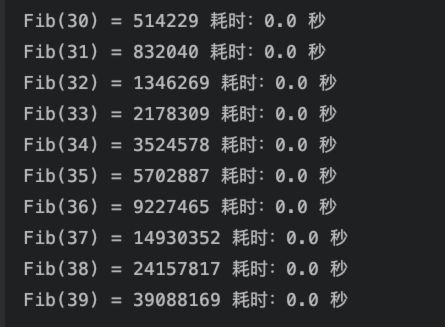
核心优化点在于:
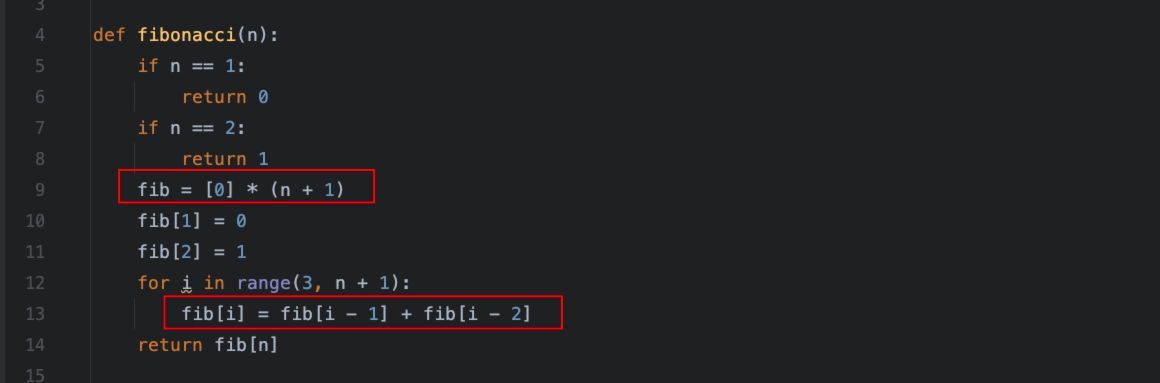
秒出,哪怕保留了4位小数,也是0秒,典型的以空间换时间的做法,而且避免了重复计算,直接从列表中取现成的就好了。所以,计算速度快了很多,几乎感知不到延迟。
效果很明显,但是,代码改动的逻辑比较大,而且,不能复用。
另一种优化方法,就是我们一直在用的装饰器了。
优化方法2:
import time
def cache(func):
mem = {}
def wrap(*args):
res = mem.get(args)
if not res:
res = mem[args] = func(*args)
return res
return wrap
@cache
def fibonacci(n):
if n == 1:
return 0
if n == 2:
return 1
return fibonacci(n - 1) + fibonacci(n - 2)
if __name__ == '__main__':
for i in range(30, 40):
start = time.time()
res = fibonacci(i)
end = time.time()
print(f"Fib({i}) = {res} 耗时:{round(end - start, 4)} 秒")
执行结果:
核心优化逻辑:
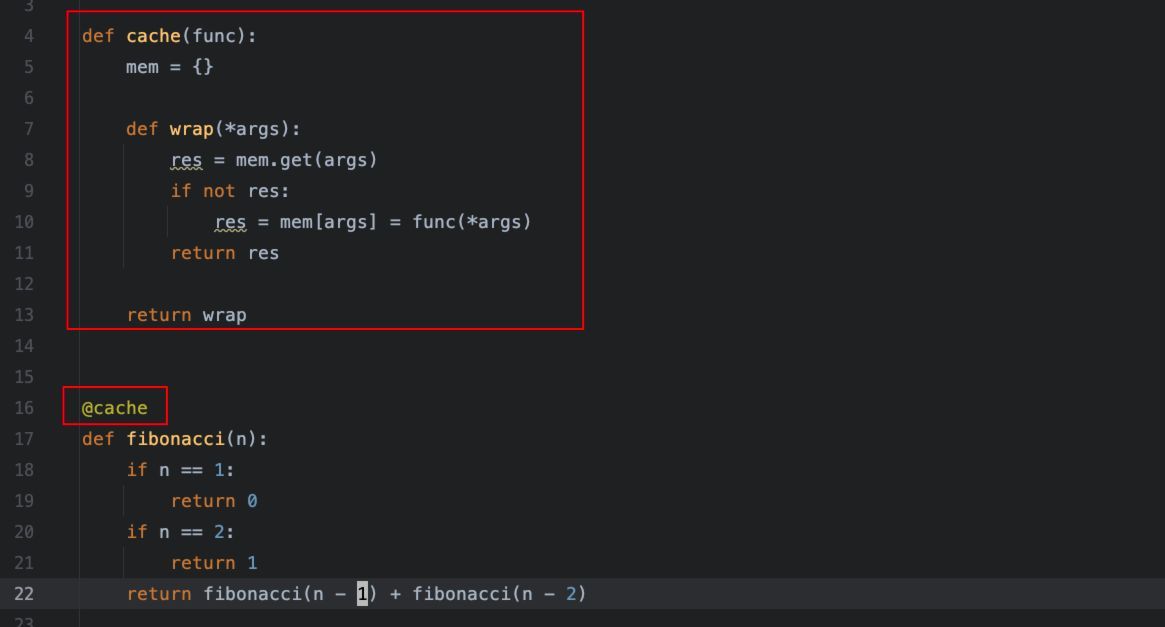
使用装饰器的优化方法,原函数无需做任何修改,可读性仍然较好,性能同样得到了提升,秒出。
而且,装饰器的实现方法,更加具备通用性,这个装饰器可以应用到其他需要缓存子问题计算结果的情况,代码的复用性更加。
总结
本文简单介绍了递归函数的概念以及递归函数的特性,然后看到了递归函数最大的问题是大量重复计算导致的性能较差的问题。最后,我们通过两个方法实现了对递归函数的性能的优化,优化的核心在于以空间换时间,规避大量的重复计算。








![[STL --stack_queue详解]stack、queue,deque,priority_queue,容器适配器](https://i-blog.csdnimg.cn/direct/7337a57b47f642d4939747b8e436af8a.png)











