以下均为python代码。先给大家看看之前文章的部分思路：

接下来我们将按照题目总体分析-背景分析-各小问分析的形式来

1 总体分析

题目提供了一个电子产品生产的案例，要求参赛者建立数学模型解决企业在生产过程中的一系列决策问题。以下是对题目的总体分析：

问题一需要企业需要从供应商购买零配件，并且需要设计一个抽样检测方案，来决定是否接受供应商提供的零配件。题目要求设计一个能够尽可能减少检测次数的方案，分别在95%和90%的置信度下，判断零配件的次品率是否超过标称值。这个问题的核心是基于统计学的抽样检验，涉及假设检验和置信区间的计算。需要考虑标称值为10%的情况下，如何设计抽样数量，使得在满足不同置信水平的条件下进行接收或拒收决策。

问题二则：在生产过程中，企业需要在多个阶段做出决策，包括：

• 是否对零配件进行检测。

• 是否对成品进行检测。

• 是否对不合格的成品进行拆解，决定是否将拆解后的零配件重新利用。

• 如何处理用户退回的不合格产品。

需要根据这些参数为企业提供决策依据，并且给出相应的指标结果。

问题3：扩展的生产决策问题

在问题2的基础上，问题3进一步扩展了生产过程，增加了多个零配件和工序的情况。题目提供了多达8个零配件和2道工序的组装过程，要求针对更复杂的生产流程给出具体的决策方案。这部分问题的复杂度更高，可能涉及到多阶段决策和动态规划。

问题4：基于抽样检测的决策调整

假设问题2和问题3中的次品率均通过抽样检测得到，要求重新进行生产过程中的决策。这一问题要求参赛者结合问题1中的抽样检测方法，重新审视生产流程中的决策，可能需要重新设计检测方案，优化成本和风险的平衡。

问题2和问题3中的各个决策环节都涉及到成本效益的权衡，需要建立一个数学模型来综合考虑检测成本、拆解费用、次品率、调换损失等。

动态规划或优化模型：面对问题3中的多工序、多零配件的复杂情况，可以使用动态规划或其他优化方法，来寻找到最优的决策路径。

2 背景分析

总结一下，题目的背景集中在生产过程中的质量控制和成本优化，企业需要在多个决策点上进行权衡，既要保证最终产品的质量，又要尽量减少生产和处理的成本损失。

3 各小问分析

这道题目是关于生产过程中的决策问题，涉及到电子产品制造中的抽样检测、装配、拆解、退换货等多个环节。问题分为四个主要部分，要求为企业设计优化生产决策的数学模型。

问题1：抽样检测方案建模与分析

该问题要求设计一个抽样检测方案，判断零配件的次品率是否超过标称值。在这个问题中，零配件次品率不会超过某个标称值（如10%）。我们需要在不同信度下，决定是否接受这批零配件。

建模目标：

我们需要设计一个抽样检测方案，确保：

1.在95%的信度下，判断零配件次品率超过标称值时拒收该批次零配件。

2.在90%的信度下，判断零配件次品率不超过标称值时接收该批次零配件。

1.抽样检测方案的基础理论

1. 假设检验 我们可以使用假设检验来进行模型设计。设： p为零配件的真实次品率。 p0为标称的次品率（10%）。 我们抽取的样本数为n，次品数为x。 根据问题要求，我们可以构建两个假设： 原假设H_0:零配件次品率p\leq p_0（零配件次品率不超过标称值，接受零配件）。 备择假设H_1:零配件次品率p>p_0（零配件次品率超过标称值，拒绝零配件）。

2. 二项分布建模 对于每个零配件，若其合格率为1-p，则每个零配件是次品的概率为p。假设我们从一批零配件中抽取了n个样本，次品的数量服从二项分布：

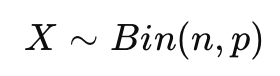
其中： n是抽样数量。 p是次品率。 X是次品的个数。 可以用正态分布近似二项分布：

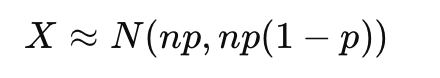
通过正态近似，可以使用标准化公式：

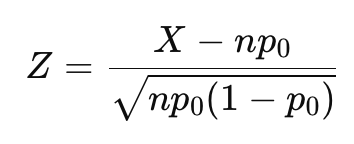
1. 双侧检验与置信区间

我们根据问题中95%和90%的信度要求进行双侧假设检验。信度要求分别对应的显著性水平alpha为：

95%信度：对应alpha=0.05。

90%信度：对应alpha=0.10。

在这两种情况下，分别计算不同显著性水平下的拒收与接收条件。

2.具体建模步骤

第一问代码：

import math
from scipy.stats import norm
import matplotlib.pyplot as plt

# 定义参数
p0 = 0.10  # 标称次品率
alpha_95 = 0.05  # 95%置信水平
alpha_90 = 0.10  # 90%置信水平
z_95 = norm.ppf(1 - alpha_95)  # 95%的临界值
z_90 = norm.ppf(1 - alpha_90)  # 90%的临界值

# 计算样本量
def calculate_sample_size(z_alpha, p0, delta):
    return math.ceil((z_alpha**2 * p0 * (1 - p0)) / delta**2)

# 假设检测误差delta为5%
delta = 0.05

# 计算样本量
n_95 = calculate_sample_size(z_95, p0, delta)
n_90 = calculate_sample_size(z_90, p0, delta)

# 打印结果
print(f"在95%的置信水平下，所需的最小样本量为: {n_95}")
print(f"在90%的置信水平下，所需的最小样本量为: {n_90}")

# 生成图表：不同显著性水平下样本量的变化
def plot_sample_size():
    alphas = [0.01 * i for i in range(5, 21)]  # 从5%到20%的不同显著性水平
    sample_sizes = [calculate_sample_size(norm.ppf(1 - alpha), p0, delta) for alpha in alphas]

    plt.figure(figsize=(8, 6))
    plt.plot(alphas, sample_sizes, marker='o', linestyle='-', color='b')
    plt.title('Sample Size vs Significance Level', fontsize=14)
    plt.xlabel('Significance Level (Alpha)', fontsize=12)
    plt.ylabel('Sample Size', fontsize=12)
    plt.axvline(x=0.05, color='r', linestyle='--', label="95% Confidence Level")
    plt.axvline(x=0.10, color='g', linestyle='--', label="90% Confidence Level")
    plt.legend()
    plt.grid(True)
    plt.tight_layout()
    plt.show()

# 生成图表：样本量与误差范围的关系
def plot_sample_size_vs_error():
    deltas = [0.01 * i for i in range(1, 21)]  # 从1%到20%的误差范围
    sample_sizes_95 = [calculate_sample_size(z_95, p0, delta) for delta in deltas]
    sample_sizes_90 = [calculate_sample_size(z_90, p0, delta) for delta in deltas]

    plt.figure(figsize=(8, 6))
    plt.plot(deltas, sample_sizes_95, label="95% Confidence Level", marker='o', linestyle='-', color='b')
    plt.plot(deltas, sample_sizes_90, label="90% Confidence Level", marker='o', linestyle='-', color='g')
    plt.title('Sample Size vs Error Margin', fontsize=14)
    plt.xlabel('Error Margin (Delta)', fontsize=12)
    plt.ylabel('Sample Size', fontsize=12)
    plt.legend()
    plt.grid(True)
    plt.tight_layout()
    plt.show()

# 运行生成图表
plot_sample_size()
plot_sample_size_vs_error()

剩余看下面的名片