题目链接: https://leetcode.cn/problems/longest-increasing-subsequence/
视频题解: https://www.bilibili.com/video/BV1RRvheFEog/
LeetCode 300. 最长递增子序列
题目描述
给你一个整数数组nums ,找到其中最长严格递增子序列的长度。
子序列是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7]是数组[0,3,1,6,2,2,7]的子序列。
举个例子:
输入: nums = [10,9,2,5,3,7,101,18]
输出: 4
解释: 最长递增子序列是[2,3,7,101],因此长度为 4。
视频题解
最长递增子序列
思路来源
思路来源
知识回顾
动态规划是一种通过将原问题分解为子问题来求解复杂问题的算法思想。它通常用于求解最优化问题,例如最长公共子序列、背包问题等。动态规划的核心思想是将原问题分解为若干个子问题,通过求解子问题的最优解推导出原问题的最优解。可以通过两点来判断一个问题能不能通过动态规划来解,一是该问题是否存在递归结构,二是对应的子问题能否记忆化。动态规划可以通过带备忘录的自上而下的递归和自下而上的迭代来分别实现。由于递归需要用到栈来实现,一些语言对递归的深度是有限制的,所以自下而上的迭代是动态规划的最佳实现方式。
思路解析
下图给出了nums = [1, 4, 3]枚举最长递增子序列的过程,每个节点都是nums的一个子序列。
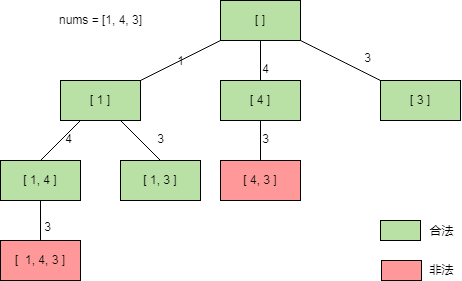
从上图可以看出题目其实就是要求从根节点到合法节点的最长路径,其中合法节点中的数组是递增序列,绿色节点表示合法节点。
下面介绍一下动态规划的解法。
动态规划的核心步骤是推导状态转移公式和边界条件处理。
首先定义dp[i]表示以nums第i个元素结尾的最长递增子序列的长度。
以nums = [1, 4, 3]这个例子我们来看下寻找最长递增子序列的过程。
- 以
第0个元素1结尾的子序列为[1],其中递增子序列为[1],所以dp[0] = 1。 - 以
第1个元素4结尾的子序列为[1, 4]、[4],其中递增子序列为[1, 4]、[4],所以dp[1] = 2。 - 以
第2个元素3结尾的子序列为[1, 3]、[1, 4, 3]、[4, 3]、[3],其中递增子序列为[1, 3]、[3],所以dp[2] = 2。
从上面可以看出我们在求dp[i]时,nums[i]需要和nums[0] ~ nums[i-1]进行比较,如果满足nums[i] > nums[k],那么dp[i] = max(dp[i], dp[k] + 1),其中0 <= k < i。
- 对于
dp[0],很显然dp[0] = 1。 - 对于
dp[1],存在nums[1] > nums[0],所以dp[1] = max(dp[1], dp[0] + 1) = 2。 - 对于
dp[2],存在nums[2] > nums[0],所以dp[2] = max(dp[2], dp[0] + 1) = 2。
扩展到一般情况可以得到状态转移公式:
dp[n] = max{dp[0] + 1, ...,dp[i] + 1,dp[n]}
其中0 <= i < n,且nums[n] > nums[i]。
接下来看下边界条件,nums的每个元素都各自为一个长度为1的子序列,故可以初始定义dp[i] = 1。
最终dp中最大的元素就是我们要找的答案。
C++代码
class Solution {
public:
int lengthOfLIS(vector<int> & nums) {
int nums_len = nums.size();
//边界条件初始化
vector<int> dp(nums_len, 1);
for (int i = 0; i < nums_len; ++i) {
for (int j = 0; j < i; ++j) {
//状态转移公式
if (nums[i] > nums[j]) {
dp[i] = max(dp[i], dp[j] + 1);
}
}
}
return *max_element(dp.begin(), dp.end());
}
};
java代码
class Solution {
public int lengthOfLIS(int[] nums) {
int nums_len = nums.length;
int max_res = 0;
// 边界条件初始化
int[] dp = new int[nums_len];
for (int i = 0; i < nums_len; ++i) {
dp[i] = 1;
max_res = Math.max(max_res, dp[i]);
}
for (int i = 0; i < nums_len; ++i) {
for (int j = 0; j < i; ++j) {
// 状态转移公式
if (nums[i] > nums[j]) {
dp[i] = Math.max(dp[i], dp[j] + 1);
max_res = Math.max(max_res, dp[i]);
}
}
}
return max_res;
}
}
python代码
class Solution:
def lengthOfLIS(self, nums: List[int]) -> int:
nums_len = len(nums)
# 边界条件初始化
dp = [1] * nums_len
for i in range(nums_len):
for j in range(i):
# 状态转移公式
if nums[i] > nums[j]:
dp[i] = max(dp[i], dp[j] + 1)
return max(dp)
复杂度分析
时间复杂度: O(n2),其中n为nums的长度。
空间复杂度: O(n), 其中n为nums的长度。