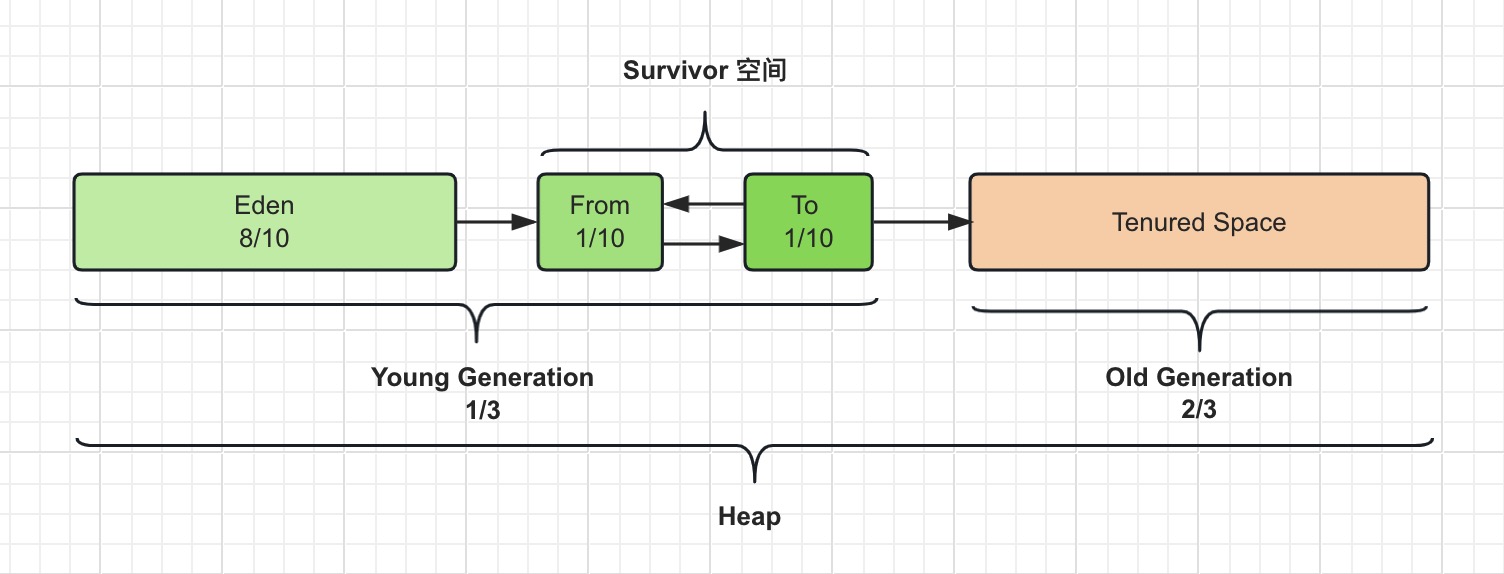
位图

问题：从40亿个没有排序的无符号整数查找一个数是否存在

1. 方法一：
   依次遍历：O(N) 太慢了

2. 排序 + 二分

1G = 1024MB = 1024 * 1024KB = 1024 1024*1024byte ~= 10亿byte。*

10亿byte是一个G，那么40亿个整形为160亿字节 ,也就是16GB的内存，那我们内存肯定放不下，但是内存却放不下。

3. 位图

$2^{32}$ = 42亿多，那么其实我们并不需要把每一个数都存储下来，我们可以使用一个bit位来表示它在不在即可，那么一个字节是8个比特位，所以我们所需要的空间为，$2^{32} /$8 ~= 5亿 ~= 500MB。那么500MB是可以接受的。

如上图，每一个蓝色方块代表的是一个整形，每个整型都有32位bit位，以第一个整型为例，我们可以表示 0~31这个范围的数字在不在，**如果在对应的bit位就变为1，如果不在对应的bit位就是0。**那我们如何直到插入的数字x是那个位置的呢？$i=x/32$，$j=x$，我们这里的$i$表示我们对应的哪个整型，而$j$表示对应的整型的哪个bit位。

位图代码实现：

namespace bit
{
	template<size_t N>
	class bitset
	{
	public:
		bitset()
		{
			_bs.resize(N/32 + 1);
		}
		void set(size_t x)
		{
			int i = x / 32;
			int j = x % 32;
			//把对应的第j个bit位变为1，其他位置不变
			//j = 4,  00000000 |= 00010000 = 00010000
			_bs[i] |= (1 << j);
		}

		void reset(size_t x)
		{
			int i = x / 32;
			int j = x % 32;
			//把对应的第j个bit位变为0，其他位置不变
			//j = 4,  00000000 &= (~00010000) -> 11101111 = 00000000
			_bs[i] &= (~(1 << j));
		}

		//验证x是否存在
		bool test(size_t x)
		{
			int i = x / 32;
			int j = x % 32;
			return (_bs[i] & (1 << j));
		}
	private:
		vector<int> _bs;
	};
}

上图的蓝色方块其实就是一个个的整型，我们创建一个vector来存储每一个整型，在创建vector的时候，我们要根据数据的范围来初始化vector大小，由于一个整型最大为42亿多，所以我们最多需要开辟134217728个整型。而我们vector是在堆区上开辟的所以也就不会存在内存不够的问题。这样查询42亿中一个数是否存在我们就可以在内存当中操控了。134217728*4 = 536,870,912 ~= 500MB。

总结一下位图：

• 优点：效率高，方便插入与删除
• 缺点：只适合整型。

如上图，库里面其实也实现了bitset，只不过它实现的方式和我们的不同，库里面直接使用一个整型来存储对应位置是否存在，所以他这里如果直接存储42亿的话还会报错，空间太大了。

布隆过滤器

布隆过滤器是由布隆（Burton Howard Bloom）在1970年提出的 一种紧凑型的、比较巧妙的概率型数据结构，特点是高效地插入和查询，可以用来告诉你 “某样东西一定不存在或者可能存在”，它是用多个哈希函数，将一个数据映射到位图结构中。此种方式不仅可以提升查询效率，也可以节省大量的内存空间

布隆过滤器是哈希表和位图的结合使用，我们使用hash函数来把字符串变为整型，让对应位图中的位置变为1。相比于传统的 List、Set、Map 等数据结构，它更高效、占用空间更少，但是缺点是其返回的结果是概率性的，而不是确切的。

实现原理：

HashMap的问题

回想一下，如果让你判断一个某个元素是否存在的时候，相信大部分人都会选择HashMap，O(1)时间就可以得出结果了，但是HashMap的缺点就是空间消耗太大了，而且由于负载因子的原因，我们数组并不能被放满，那么当数据量很大例如上亿的时候，所需内存空间也很大。

布隆过滤器结果

布隆过滤器跟位图的一样的，如下图：

和位图不一样的是，我们的位置是由哈希函数算出来的，所以我们不单单可以使用整型也可以使用字符串，通过对应的哈希函数转为整型，而由于字符串哈希函数可能会（"abcba）和（“caabb”）产生冲突，我们一般一个元素会有多个哈希函数来计算出不同的位置，这样可以降低冲突几率。

如上图，我们"abandon"通过三个哈希函数算出来的位置为：$[3,8,12]$，而$"baidu"$通过三个函数算出来的位置为：$[5,8,10]$，这也就代表了我们这个位置可能会被别的字符串占用，这也就导致了我们布隆过滤器可能会出现误判的情况。

例如：随着数据量的增加，我们即是内存里面并没有$"apple"$这个字符串，但是通过哈希函数算出来的位置都被别人占完了，所以 即是内存里面并没有这个元素，返回的结果也可能为有。

同时布隆过滤器还有几个公式：

m : 表示布隆过滤器中bit的位数

n：表示插入元素的个数

k：表示哈希函数的个数

结论：

当哈希函数个数固定的时候我们有一个结论：$(误判率)f(k)=(1-\frac{1}{e^{\frac{nk}{m}}}{)}^k$这就意味着我们的n越大，我们的分母越大，整个数越小，1-这个数就越大，所以误判率就越大，而我们的m越大我们的误判率越小。 m/n越大，误判率越小。

当我们的n和m固定的时候，$k=\frac{m}{n}ln2$ 误判率最小。

当我们误判率p和插入个数n去确定的情况下，通过期望的误判率和插入个数可以得出来我们的bit长度为：$m=-\frac{nlnp}{(ln2{)}^2}$。

代码实现：

//三个哈希函数
struct BKDRHash
{
	size_t operator()(const string& s)
	{
		// BKDR
		size_t value = 0;
		for (auto ch : s)
		{
			value *= 31;
			value += ch;
		}
		return value;
	}
};

struct DJBHash
{
	size_t operator()(const string& s)
	{
		size_t hash = 5381;
		for (auto ch : s)
		{
			hash += (hash << 5) + ch;
		}
		return hash;
	}
};

struct APHash
{
	size_t operator()(const string& s)
	{
		size_t hash = 0;
		for (long i = 0; i < s.size(); i++)
		{
			if ((i & 1) == 0)
			{
				hash ^= ((hash << 7) ^ s[i] ^ (hash >> 3));
			}
			else
			{
				hash ^= (~((hash << 11) ^ s[i] ^ (hash >> 5)));
			}
		}
		return hash;
	}
};

namespace bit
{
	//N表示插入个数，X表示 M / N (M为bit长度)
	template<size_t N,
			size_t X = 5,
			class K = string,
			class Hash1 = BKDRHash,
			class Hash2 = DJBHash,
			class Hash3 = APHash>
	class boolmfilter
	{
	public:
		void set(const K& key)
		{
			size_t M = N * X;
			//分别求出对应的整型
			size_t hash1 = Hash1()(key) % M;
			size_t hash2 = Hash2()(key) % M;
			size_t hash3 = Hash3()(key) % M;

			//设置到位图当中
			_bs.set(hash1);
			_bs.set(hash2);
			_bs.set(hash3);
		}

		bool test(const K& key)
		{
			size_t M = N * X;
			//三个位置当中只要有一个位置不存在，那么这个元素一定不存在。
			size_t hash1 = Hash1()(key) % M; //不能超过bit数组可容纳的长度
			if (!_bs.test(hash1))
				return false;
			size_t hash2 = Hash2()(key) % M;
			if (!_bs.test(hash2))
				return false;
			size_t hash3 = Hash3()(key) % M;
			if (!_bs.test(hash3))
				return false;

			//如果三个位置都存在也不一定存在，可能是其他元素把位置占完了。
			return true;
		}
	private:
		bit::bitset<N*X> _bs;
	};
}

void Test_boolmfilter()
{
	string s1("apple");
	string s2("banana");
	string s3("pear");

	bit::boolmfilter<10> bs1;
	bs1.set(s1);
	bs1.set(s2);
	bs1.set(s3);

	//前三个在，后三个不在
	cout << bs1.test(s1) << endl;
	cout << bs1.test(s2) << endl;
	cout << bs1.test(s3) << endl;
	cout << bs1.test("aaaa") << endl;
	cout << bs1.test("bbbb") << endl;
	cout << bs1.test("cccc") << endl;
}

当然了想要测出来本来不在的却输出在我们还需要更多的数据，这里数据太少了测不出来。

//测试相似误判和不相似误判
void Test_BoolFilter()
{
	srand(time(0));
	const int N = 1000000;
	vector<string> v;
	
    //原始数据
	bit::boolmfilter<N> bs;
	string url = "https://blog.csdn.net/anjibgdexuexi?type=blog";
	for (int i = 0; i < N; i++)
	{
		v.push_back(url + std::to_string(i));
	}
	for (auto& e : v) bs.set(e);

	v.clear();
	//相似数据，相同前缀，不同后缀
	for (int i = 0; i < N; i++)
	{
		string nurl = url;
		nurl += std::to_string(9999999 + i);
		v.push_back(nurl);
	}
	int n = 0;
	for (auto& e : v)
	{
		if (bs.test(e))
			n++;
	}
	cout << "相似字符串误判率：" << (double)n / (double)N << endl;

	v.clear();

	//不相似，前后缀都不一样
	for (int i = 0; i < N; i++)
	{
		string str = "孙悟空";
		str += std::to_string(rand() + i);
		v.push_back(str);
	}

	int n1 = 0;
	for (auto& e : v)
	{
		if (bs.test(e))
			n1++;
	}
	cout << "不相似字符串误判率：" << (double)n1 / (double)N << endl;
}

上段测试代码，我们就可以看到布隆过滤器的误判率了，同时当我们m/n越大我们误判率就越小。

海量数据处理

位图应用

• 给定100亿个整数，设计算法找到只出现一次的整数？

因为有一百亿个整数，但是由于整数最大的值就是42亿多，所以我们设置bit位长度的时候只需要设置$2^{32}$即可。剩下的大量的重复值。当我们需要记录某个元素的出现次数的时候我们一般想到的都是哈希表，这里数据量太大内存肯定是不够的，所以我们可以使用位图。上述我们位图每个元素用一个bit位来表示在不在。

那么这里的话我们只需要使用两个bit位来表示：

1. 如果两个bit位都是0，说明不在
2. 如果第一个为0，第二个为1，表示出现了一次
3. 如果第一个为1，第二个为0，表示出现了2次
4. 如果两个都为1，表示出现了三次及以上

代码实现：以下代码对于超过两次的统一设置为3次。

template<size_t N>
	class twobitset
	{
	public:
		twobitset()
		{
			_bs.resize(N / 32 + 1);
		}
		void set(size_t x)
		{
			int i = x / 16;
			int j = x % 16;
			//第j位和j+16位来表示
			int one = (_bs[i] & (1 << (j+16))) > 0; //获取第j+16位
			int two = (_bs[i] & (1 << j)) > 0;       //获取第j位
			if (one == 0 && two == 0) // 00 ->01
			{
				_bs[i] |= (1 << j);
			}
			else if (one == 0 && two == 1) // 01 -> 10
			{
				_bs[i] &= (~(1 << j));
				_bs[i] |= (1 << (j + 16));
			}
			else if (one == 1 && two == 0) // 10 -> 11
			{
				_bs[i] |= (1 << j);
			}
		}
		//验证x是否存在
		int test(size_t x)
		{
			int i = x / 16;
			int j = x % 16;

			//第j位和j+16位来表示
			int one = (_bs[i] & (1 << (j + 16))) > 0; //获取第j+16位
			int two = (_bs[i] & (1 << j)) > 0;       //获取第j位

			if (one == 0 && two == 0) // 00 ->01
			{
				return 0;
			}
			else if (one == 0 && two == 1) // 01 -> 10
			{
				return 1;
			}
			else if (one == 1 && two == 0) // 10 -> 11
			{
				return 2;
			}
			else
				return 3;
		}
	private:
		vector<int> _bs;
	};

如上段代码，我们用每个整型的前16个bit位和后16个bit位表示出现的次数。但其实还有另一种实现方式，我们直接使用两个位图，那么次数还是一样的变化过程，而且比我们上面这种方式要简单很多，直接复用位图的成员函数。

代码实现：

	template<size_t N>
	class twobitset
	{
	public:
		void set(size_t x)
		{
			if (_bs1.test(x) == 0 && _bs2.test(x) == 0) // 00 ->01
			{
				_bs2.set(x);
			}
			else if (_bs1.test(x) == 0 && _bs2.test(x) == 1) // 01 -> 10
			{
				_bs2.reset(x);
				_bs1.set(x);
			}
			else if (_bs1.test(x) == 1 && _bs2.test(x) == 0) // 10 -> 11
			{
				_bs2.set(x);
			}
			//超过两次的这里不处理
		}
		//验证x是否存在
		int test(size_t x)
		{

			if (_bs1.test(x) == 0 && _bs2.test(x) == 0) // 00 
			{
				return 0;
			}
			else if (_bs1.test(x) == 0 && _bs2.test(x) == 1) // 01 
			{
				return 1;

			}
			else if (_bs1.test(x) == 1 && _bs2.test(x) == 0) // 10 
			{
				return 2;

			}
			else
				return 3;
		}
	private:
        //直接复用位图
		bit::bitset<N> _bs1; 
		bit::bitset<N> _bs2;
	};
}

• 给两个文件，分别有100亿个整数，我们只有1G内存，如何找到两个文件交集？

使用位图遍历其中一个文件，统计每个元素是否存在，然后再依次遍历另一个文件，如果在位图中，则 加入到交集里面。

• 位图应用变形：1个文件有100亿个int，1G内存，设计算法找到出现次数不超过2次的所有整数

如上段代码，都已次数小于等于2的即可。

布隆过滤器应用

• 给两个文件，分别有100亿个query（查询字符串），我们只有1G内存，如何找到两个文件交集？ 假设每一个query都有50个字节，那么一共有5000亿字节 ~= 500G内存，那如何做呢？

1. 平均分成1000个小文件。

如上图，我们把大文件A和大文件B均分为1000个小文件，然后再进行查找交集，但是这里有均分会有一个问题，我们A0需要去和$B0,B\mathrm{1...}B999$每一个都要去找交集，A1也是一样那么这里就是$O(N^2)$的时间复杂度。

2. 哈希切分

我们通过哈希函数求出每个$query$然后对1000取模，就可以求出这1000个小文件对应的坐标，那么我们$Ai$小文件就不需要每个都要和$Bi$小文件去查交集了。

因为我们相同字符串通过哈希函数%1000一定求出来的是同一个坐标，不可能求出来的坐标不同，所以我们$Ai$只需和对应的$Bi$去找交集即可，这样时间复杂度有$O(N^2)->O(N)$。不过这里有个缺陷，由于布隆过滤器会出现误判的情况，对与交集我们肯定不会错，但是不是交集的可能也被误判进去了O.o?。

但是哈希切分还有一个问题，那就是有可能其中一个文件特别大，几G或者几十G都有可能（重复值过多或求出来的哈希值一样），本质上都是哈希冲突，那怎么办呢？

针对这个问题可以进行二次划分，再使用一个新的哈希函数进行求坐标。就是当一个文件的内容太大的时候，在对这个$Ai$划分为多个$AAi$，于此同时我们对应的$Bi$也需要划分为多个$BBi$。但其实我们可以不管这个问题，无论文件多么的大，我们都直接使用set插入即可。

我们set插入失败只有两种可能：1. query已存在。2. 内存不够，那么如果是重复值过多的情况下，由于set的特性就可以解决，如果真的就是哈希函数不行，我们不同的值也很多， 那么单独对这个文件再换一个哈希函数进行重新划分即可。