由 AI 生成：过度简化的树、引导聚合、集成方法、弱学习器、减少方差

集成方法 — 数量，而不是质量

一、说明

        机器学习中的集成方法是指组合多个模型以提高预测性能的技术。集成方法背后的基本思想是聚合多个基础模型（通常称为弱学习器）的预测，以生成通常比任何单个模型更准确、更稳健的最终预测。一般而言，我们通常遵循质量胜于数量的原则。然而，在这种情况下，事实证明相反的原理同样有效。

二、何为集成方法

集成方法通常分为两类：

1. Bagging：
   这种方法涉及在训练数据的不同子集上训练同一基础学习算法的多个实例。集成中的每个模型都独立学习，然后通常通过平均或投票来组合它们的预测，以做出最终预测。
2. 提升：
   提升的工作原理是按顺序训练一系列较弱的学习器，其中每个后续模型都侧重于前一个模型难以处理的示例。最终预测通常是每个弱学习器所做预测的加权总和。

        常见的集成方法包括 Random Forest、AdaBoost、Gradient Boosting Machines 或 Extreme Gradient Boosting。这些方法由于能够提高预测准确性和泛化性能而广泛用于各种机器学习任务。

        在本文中，我们将仔细研究第一种方法，即 bagging。

三、什么是装袋？— 简短介绍

        装袋 （Bootstrap aggregating） 是机器学习中的一种技术，在这种技术中，我们创建模型的多个副本，并在训练数据的不同子集上训练每个副本。这些子集是通过随机选择带有替换的样本来创建的（这就是 “bootstrap” 部分的用武之地）。训练每个模型后，它们的预测以某种方式组合起来，以做出最终预测。
Bagging 通过对多个模型进行平均或投票来帮助减少预测的方差，与单独使用单个模型相比，可以获得更稳定、更准确的预测。

        想象一下，您正在尝试猜测罐子中的糖果数量。如果你只问一个朋友猜，他们可能会差很多。但是，如果你问几个朋友，每个朋友都有不同的观点和猜测方式，然后你平均他们的猜测，你可能会得到一个更准确的估计。

四、如何减少方差？

        正如我们之前提到的，装袋是一种减少方差的方法。它基于一个简单的观察。
        假设我们有 n 个独立随机变量 X1,...,Xn，具有相同的方差 σ^2。这些变量中的每一个都对应于每个弱学习器的预测。如果我们对所有较弱的学习器的结果进行平均，会怎么样？
设 X ― 是所有弱学习器的平均值。让我们看看这样一个随机变量的方差将如何变化。

        所以，我们想找到

        我们来做一些计算。根据方差的属性

        由于变量 习 是独立的，我们可以写成：

但是，所有随机变量 X1,...,Xn 具有相同的方差 σ^2，因此：

因此

        对一组观测值求平均值可以减少方差。因此，减少方差从而提高给定学习方法的预测准确性的自然方法是从总体中提取多个训练集，使用每个训练集构建单独的预测模型，然后对结果预测进行平均。

五、装袋如何运作？

        简而言之，我们使用 K 个不同的训练集 （S1,...,Sk） 构建 K 模型 （f1,...,fk）。每个模型 fi 都在不同的 si 集上训练。然后，我们将所有 K 模型获得的结果平均，以获得具有低方差的单个统计模型

        不幸的是，在实践中，通常很难获得这么多不同的训练集。我们经常为数据太少的问题而苦苦挣扎。在这种情况下，我们该怎么办？正如您可能已经猜到的那样，“bootstrap 聚合”这个名称揭示了我们如何处理获取不同训练数据集的问题 — 执行 bootstrap 采样。

Bootstrap 抽样只不过是带替换的随机抽样。

带替换的随机抽样是从数据集中随机选择项目的过程，每次选择后，该项目都会放回数据集中。这意味着在抽样过程中可以多次选择同一项目。

        因此，在 bagging 方法中，或者更准确地说是 bootstrap 聚合，我们使用 k 个 bootstrap 样本构建 k 个模型，然后我们对所有模型获得的结果进行平均以获得单个预测。

六、副作用 — “Out of Bag” 集

        事实证明，在引导过程中，平均只有大约 2/3 的观察值用于构建树。在树构建期间未使用的观测值称为 OOB 外 （OOB） 观测值。

        因此，如果我们执行 bootstrap K 次，那么对于平均 K/3 个观测值，树没有使用该观测值。我们可以使用这些树来估计预测误差，方法是取这些树的平均误差。OOB 估计的总误差（作为所有观测值的平均误差）是检验误差的良好近似值。

        为什么 1/3 的观察结果没有用于树木构建过程？

        假设我们有 n 个观测值。然后，不选择单个观测值的概率相等

        如果我们用替换 n 次来绘制它们，那么概率为

        限制中的内容（或实际上对于大 n）给出了大约

七、示例

        让我们从生成人工数据集开始。

        数据是一维的，表示由方程 y=xsin（x） 描述的区间 [0,10] 上的函数，其中添加了一些随机噪声。

        首先，我们需要确定我们想要构建多少个估计器（模型）（即，我们需要指定数字 K）。假设 K=3。
        现在，我们将演示 bootstrap 的工作原理。
        在 bootstrap 中，目标是使用替换对观测值进行随机采样。在我们的例子中，我们为每个模型分别绘制了三次训练样本。
        由于我们正在使用替换进行绘制，因此某些观测值可能根本不会绘制，而其他观测值可能会绘制多次。黄色越强烈，绘制给定观测值的次数就越多。

        现在，我们为每个样本分别训练一个单独的估计器（在我们的例子中，它是一个决策树）。这样，我们将获得三种回归树模型。
        我们将将它们全部显示在一个图上，以便更好地可视化它们之间的差异。

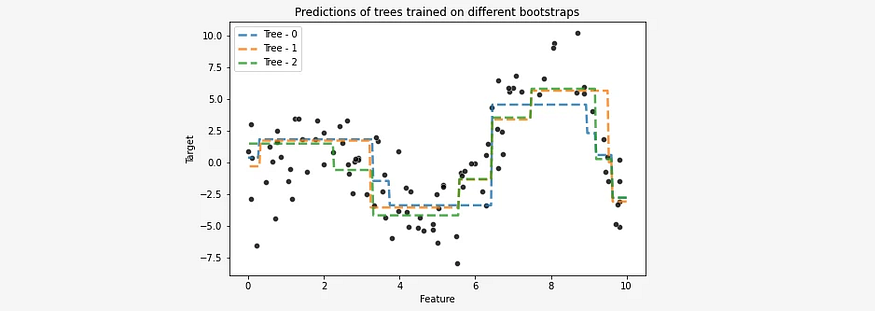
通过聚合结果，即从所有 3 棵树中获取平均预测值，我们得到最终模型。

        例如，让我们看看基于不同 bootstrap 样本构建的每棵树对值 x=8 的预测：
Tree 0： 4.54997803
Tree 1： 5.64685022
Tree 2： 5.79985777
最终模型只是各个分量结果的平均值，因此：

八、实现

        幸运的是，我们不必手动完成所有这些操作。我们得到了流行的 sklearn 模块中的实现的帮助。
        我们只需要选择估计器 — 在我们的例子中，它是一个回归树，以及这些估计器的数量，这些估计器是我们想要构建的模型，然后对它们的结果进行平均。

from sklearn.ensemble import BaggingRegressor
from sklearn.tree import DecisionTreeRegressor

bagged_trees = BaggingRegressor(
    base_estimator=DecisionTreeRegressor(max_depth=3),
    n_estimators=3,
    )
bagged_trees.fit(data_train, target_train)

使用 sklearn 中的 BaggingRegressor 的结果如下：

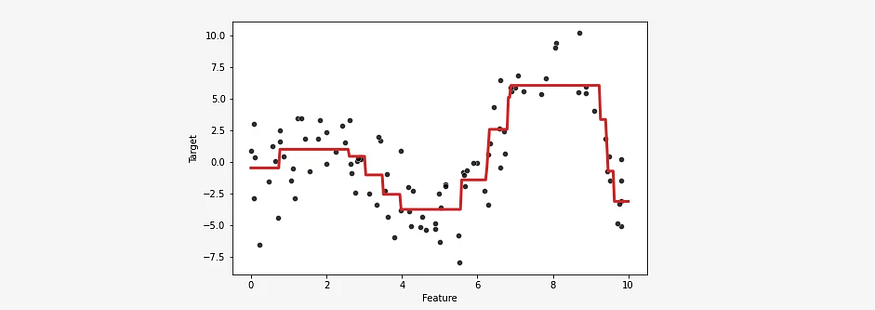
下次见！