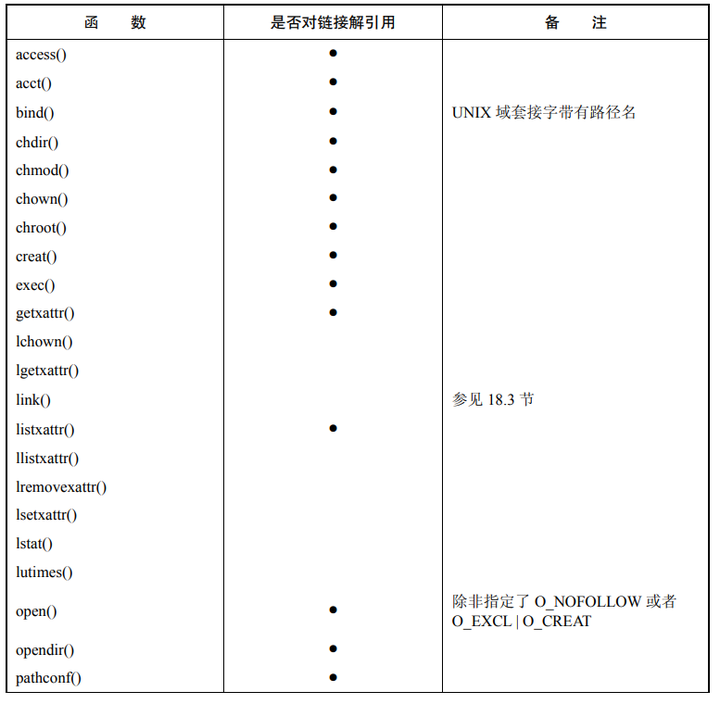
专题名称
第1讲(3 小时)
动态面板模型
面板 VAR 模型
授课内容
一阶差分GMM 估计量(FD-GMM)
序列相关检验、过度识别检验(Sargan 检验)
模型设定常见问题(弱工具变量问题)
面板 VAR 模型简介
允许外生变量的PVAR模型
冲击反应函数(IRF)、方差分解(FEVD)
应用实例(介绍2篇论文)


主要是y会受到上一期y的影响
DGP:data generation process
y
t
,
y
t
−
1
,
y
t
−
2
y_t,y_{t-1},y_{t-2}
yt,yt−1,yt−2



这几篇文献都是比较经典的,如果要研究的话,可以查看他们的研究分支,也就是后续人的研究。

资本结构动态调整文献,也就是为什么要假设为动态面板模型。

动态面板检验的三个思路

记住相关性



什么是矩条件?
关于IV的例子:学生面试-老师是认识-换个不认识的老师
这个例子是一个很好的例子
作为工具变量,必须满足下述四个条件: (1)与所替的随机解释变量高度相关; (2)与 随机误差项 不相关; (3)与模型中其他解释变量不相关; (4)同一模型中需要引入多个工具变量时,这些工具变量之间不相关。

如何在stata中使用工具变量估计(1a)

2SLS 二阶段最小二乘法的思想:其实就是找IV进行平均,回想一下学生面试的例子

GMM的出现,就是IV可能与干扰项相关呢?

- 主要是回归过程
- 注意small命令,这是针对小样本的调整,就是自由度的问题,是n还是n-k(k是变量个数)

2SLS与GMM的区别
前者是寻找参数,使矩条件尽可能被满足;后者是寻找参数,最大化或最小化一个目标函数(求极值) 换句话说:就是对替换的“老师”,按相关性,给一个权重,然后求极值。或者2SLS就是一个等权重的特例。 - 2SLS与GMM的估计代码示例
-
g
a
m
2
s
f
i
r
s
t
gam2s first
gam2sfirst这是为报告出2阶段的GMM

结果对比

- 这里告诉我们:动态面板至少是4年的数据






这里说明:2SLS就是GMM的特例

- 方差是为了保证权重是正的,而z*u不一定是正的。


代码实操环节
- 这里产生了随机模拟的“上帝公式”

- OLS、FE、GMM估计的对比结果



FD-GMM一阶差分-GMM估计

- 对stata基本语言的解释
global xx"(0/1).wL(0/2).(k ys) yr1980-yr1984"
xtabond n $
xxest store ab 0

- 序列相关检验

不看order1 只看order2的p值,并且应该是不显著的。

过度识别检验
要求最后的检验是不显著的,R2越低越好,有一个显著也没关系,删除一个即可。

twostep一定要加

序列自相关和过度识别检验是必须的,两者不显著才好。
robust和twostep
计算的是不同的哦

同模型设定要正确 ->sargan
统计推断 ->robust
老师说要跑两遍
1.就是加twostep
2.删掉twostep,加上robust进行系数的标准误估计


弱工具变量
一个比方:幼儿园的奖状来证明你的科研能力 太弱了
一个结论:一般选五个(在T很大的时候)

tips
在用SYS-GMM时,通常Sargan和序列相关的检验都通过不了(显著)
尽量在系数小于0.8-0.9的话,用FD-GMM即可。
PVAR (Panel Vetor Auto Regression )
一个动态变化的系统
用一个系统性思维去思考问题。
- RIF 脉冲分析 政策模拟
- Granger因果检验 因果检验
- 方差分解
Recentered influence function
这图是VAR的几块分析

- 因果检验的解释 , 在控制其他项的情况下,式子1:y不是x的granger因,式子2:x是y的Granger因。
- 为何要放多期的滞后性?政策具有滞后项。
那么什么是PVAR
比VAR多了一个个体
那么第一步就想怎么除去这个个体效应

给出了四种方法。重点是ForD
改进的命令

面板PVAR的前提要求:
- 变量是平稳的哦
- 需要做panel的单位根检验哦
- 不平稳-取对数-差分处理
不平稳就是协整检验

lag(2)的解释

 #### 滞后阶数的选择
#### 滞后阶数的选择
会损失自由度,虽然可以避免模型的偏误(捕捉可能的政策滞后效应),但参数的估计可能有偏误。所有,基于信息准则进行权衡。


- AIC-惩罚力度大,倾向于解释变量多 - 避免遗漏变量。
- BIC-惩罚力度小,倾向于解释变量少-阶数少。
- HQIC介于两者之间。


通常:以BIC为准。

最好还往后面推一期。
脉冲分析impulse response
- 怎么看显著性?看线条是否跨过了0轴
- 红色线就是变动值,绿、蓝是区间线。


方差分解

- 结果怎么看?
纵向固定一个变量,随着年份看看其余变量(横向)对固定变量的影响。