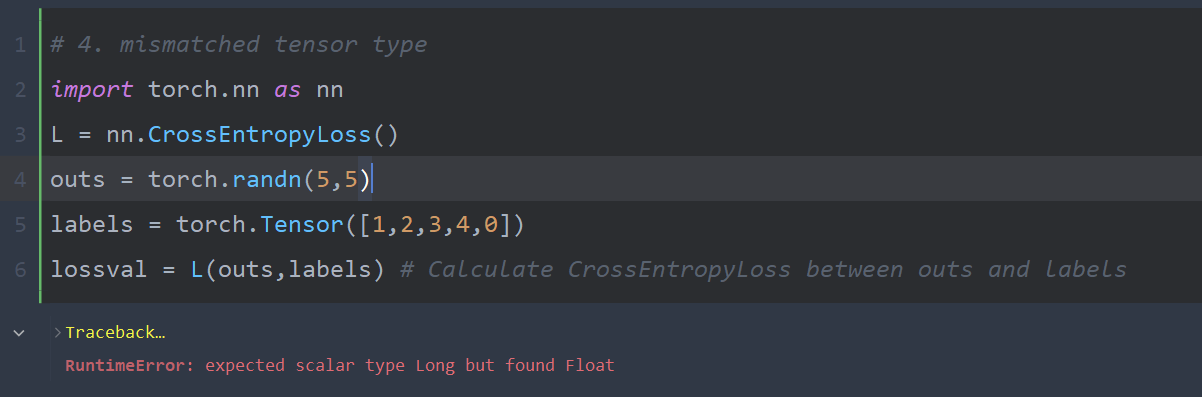
第一种形式很常见

多元正态分布

多元正态分布（Multivariate Normal Distribution），也称为多变量正态分布或多维正态分布，是统计学中一种重要的概率分布，用于描述多个随机变量的联合分布。

假设有 $n$ 个随机变量 $X_1,X_2,\dots ,X_n$，它们服从多元正态分布，则这 $n$ 个随机变量的联合概率密度函数（PDF）可以表示为：

$$f(x_1,x_2,\dots ,x_n)=\frac{1}{\sqrt{(2\pi {)}^n|\Sigma |}}\exp \left(-\frac{1}{2}(x-\mu {)}^{\top }{\Sigma }^{-1}(x-\mu )\right)$$

其中：

• $x=(x_1,x_2,\dots ,x_n{)}^{\top }$ 是一个 $n\times 1$ 的列向量，表示 $n$ 个随机变量的观测值。
• $\mu =({\mu }_1,{\mu }_2,\dots ,{\mu }_n{)}^{\top }$ 是一个 $n\times 1$ 的列向量，表示 $n$ 个随机变量的均值。
• $\Sigma$ 是一个 $n\times n$ 的对称正定矩阵，称为协方差矩阵，其元素 ${\sigma }_{ij}$ 表示 $X_i$ 和 $X_j$ 之间的协方差。
• $|\Sigma |$ 表示协方差矩阵 $\Sigma$ 的行列式。
• ${\Sigma }^{-1}$ 是协方差矩阵 $\Sigma$ 的逆矩阵。
• $(x-\mu {)}^{\top }$ 是 $(x-\mu )$ 的转置。

二维高斯函数（也称为二维正态分布函数）是统计学和物理学中常用的一个函数，用于描述二维空间中的随机变量的分布。这里我们讨论两种形式的二维高斯函数，其中第二种形式通过几何变换（如旋转和平移）从第一种形式推导出来。

二元正态分布

在二元正态分布中，如果已知两个变量$X$和$Y$的相关系数$\rho$以及它们的标准差${\sigma }_X$和${\sigma }_Y$，那么协方差矩阵$\Sigma$可以表示为：

$$\Sigma =\left(\begin{array}{cc}{\sigma }_X^2& \rho {\sigma }_X{\sigma }_Y\\ \rho {\sigma }_X{\sigma }_Y& {\sigma }_Y^2\end{array}\right)$$

这里，${\sigma }_X^2$和${\sigma }_Y^2$分别是$X$和$Y$的方差，而$\rho {\sigma }_X{\sigma }_Y$是它们的协方差。

接下来，需要计算这个协方差矩阵的逆矩阵${\Sigma }^{-1}$。首先，计算协方差矩阵的行列式$|\Sigma |$：

$$|\Sigma |={\sigma }_X^2{\sigma }_Y^2-(\rho {\sigma }_X{\sigma }_Y{)}^2={\sigma }_X^2{\sigma }_Y^2(1-{\rho }^2)$$

然后，利用行列式的值和协方差矩阵的元素来构造逆矩阵。逆矩阵${\Sigma }^{-1}$的元素可以表示为：

$${\Sigma }^{-1}=\frac{1}{|\Sigma |}\left(\begin{array}{cc}{\sigma }_Y^2& -\rho {\sigma }_X{\sigma }_Y\\ -\rho {\sigma }_X{\sigma }_Y& {\sigma }_X^2\end{array}\right)$$

将行列式的值代入上式，得到：

$${\Sigma }^{-1}=\frac{1}{{\sigma }_X^2{\sigma }_Y^2(1-{\rho }^2)}\left(\begin{array}{cc}{\sigma }_Y^2& -\rho {\sigma }_X{\sigma }_Y\\ -\rho {\sigma }_X{\sigma }_Y& {\sigma }_X^2\end{array}\right)$$

进一步化简，得到：

$${\Sigma }^{-1}=\frac{1}{1-{\rho }^2}\left(\begin{array}{cc}\frac{1}{{\sigma }_X^2}& -\frac{\rho }{{\sigma }_X{\sigma }_Y}\\ -\frac{\rho }{{\sigma }_X{\sigma }_Y}& \frac{1}{{\sigma }_Y^2}\end{array}\right)$$

这个逆矩阵代入多元正态分布就是第一种形式。

第一种形式：标准二维高斯函数

标准二维高斯函数（也称为二维正态分布的概率密度函数）的表达式为：

$$f(x,y)=\frac{1}{2\pi {\sigma }_x{\sigma }_y\sqrt{1-{\rho }^2}}\exp \left(-\frac{1}{2(1-{\rho }^2)}\left[{\left(\frac{x-{\mu }_x}{{\sigma }_x}\right)}^2-2\rho \left(\frac{x-{\mu }_x}{{\sigma }_x}\right)\left(\frac{y-{\mu }_y}{{\sigma }_y}\right)+{\left(\frac{y-{\mu }_y}{{\sigma }_y}\right)}^2\right]\right)$$

其中，

• ${\mu }_x$ 和 ${\mu }_y$ 分别是 $x$ 和 $y$ 的均值（位置参数）。
• ${\sigma }_x$ 和 ${\sigma }_y$ 分别是 $x$ 和 $y$ 的标准差（尺度参数）。
• $\rho$ 是 $x$ 和 $y$ 的相关系数（形状参数）。

第二种出现在Gabor滤波器中，第二种又有多种变形，认清它是高斯函数。

Gabor函数

Gabor滤波器是一种基于Gabor函数的特定频率和方向选择性滤波器，是一种用于图像纹理分析和特征提取的线性滤波器，由Dennis Gabor于1946年提出，广泛应用于图像处理和计算机视觉领域。在空间域中，一个二维Gabor滤波器可以看作是一个正弦平面波和高斯核函数的乘积。

$$g(x,y;\lambda ,\theta ,\psi ,\sigma ,\gamma )=\exp \left(-\frac{x^{\prime 2}+{\gamma }^2{y}^{\prime 2}}{2{\sigma }^2}\right)\cos \left(2\pi \frac{x^{\prime }}{\lambda }+\psi \right)$$

其中，

• $(x,y)$ 是图像中像素的坐标。
• $\lambda$ 是正弦函数的波长。
• $\theta$ 是Gabor核函数的方向，表示Gabor函数平行条纹的方向。
• $\psi$ 是相位偏移，通常设置为0或$\frac{\pi }{2}$。
• $\sigma$ 是高斯函数的标准差，决定了Gabor滤波器的带宽。
• $\gamma$ 是空间纵横比，决定了Gabor滤波器的椭圆率。当$\gamma =1$时，滤波器形状是圆的；当$\gamma <1$时，滤波器形状沿平行于$\theta$的方向拉长。

$x^{\prime }$ 和 $y^{\prime }$ 是通过旋转坐标轴得到的坐标，它们与原始坐标$(x,y)$的关系为：

$$\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)=\left(\begin{array}{cc}\cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)$$

这个旋转矩阵用于将Gabor滤波器的方向调整到$\theta$指定的角度。

Gabor滤波器的一个重要特性是它能够捕捉图像中特定频率和方向的信息。通过调整$\lambda$、$\theta$、$\sigma$和$\gamma$等参数，可以生成一系列具有不同频率和方向选择性的Gabor滤波器，从而用于图像的纹理分析和特征提取。

在实际应用中，通常会使用多个Gabor滤波器（具有不同的参数组合）对图像进行滤波，然后分析滤波后的图像以提取有用的特征信息。

第二种形式高斯函数

1

$f(x,y)=A\exp \left(-\frac{x^{\prime 2}+{\gamma }^2{y}^{\prime 2}}{2{\sigma }^2}\right)$是高斯函数，可由标准正态分布通过几何变换推出。

2

也可以写为
$$f(x,y)=A{\mathrm{e}}^{-\frac{1}{2}\left(\frac{{\acute{x}}^2}{{\sigma }_x^2}+\frac{{\acute{x}}^2}{{\sigma }_y^2}\right)}$$

${\sigma }_x$和${\sigma }_y$为$x$和$y$方向上高斯函数的标准差，$\gamma ={\sigma }_x/{\sigma }_y$表示高斯函数的椭圆率。

滤波器在$x$方向上的“宽度”可以由标准差${\sigma }_x$控制，而在$y$方向上的“宽度”可以由另一个标准差${\sigma }_y$控制。但在实际应用中，我们并不直接设置这两个标准差，而是通过设置一个主标准差$\sigma$和一个空间纵横比$\gamma$来间接控制。

空间纵横比$\gamma$定义了滤波器在$x$和$y$方向上的相对“宽度”。当$\gamma =1$时，滤波器是圆形的；当$\gamma <1$时，滤波器在$y$方向上的“宽度”比$x$方向小，形成椭圆形，且椭圆的长轴与$x$轴平行；当$\gamma >1$时，情况相反。

在Gabor滤波器的标准定义中，通常只关注一个标准差$\sigma$和一个空间纵横比$\gamma$。这两个参数共同决定了滤波器在不同方向上的形状和带宽。

3

将$f(x,y)$写成关于$x$和$y$的函数，这是一个指数项有交叉项的形式。

$$z=A{e}^{-\left[a(x-{\mu }_x{)}^2+2b(x-{\mu }_x)(y-{\mu }_y)+c(y-{\mu }_y{)}^2\right]}$$

其中，

• $a=\frac{{\cos }^2\theta }{2{\delta }_x^2}+\frac{{\sin }^2\theta }{2{\delta }_y^2}$
• $b=-\frac{\sin (2\theta )}{4{\delta }_x^2}+\frac{\sin (2\theta )}{4{\delta }_y^2}$
• $c=\frac{{\sin }^2\theta }{2{\delta }_x^2}+\frac{{\cos }^2\theta }{2{\delta }_y^2}$