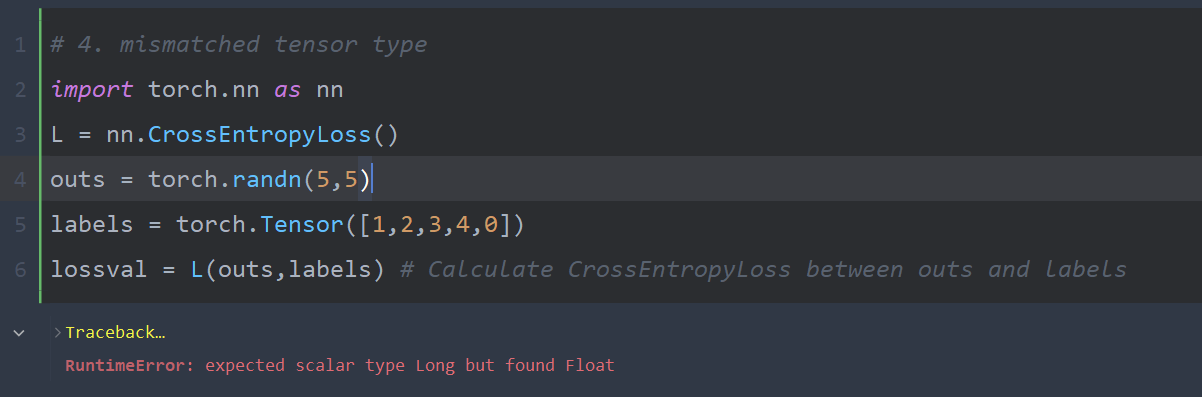
卷积神经网络(CNN)
深度卷积神经网络中,有如下特性
- 很多层(Compositionality,组合性):
深度卷积神经网络通常由多层卷积和非线性激活函数组成。这种多层结构使得网络能够逐步提取和组合低层次的特征(如边缘、纹理)到高层次的特征(如物体的部件和整体),从而实现对复杂模式的表达和识别。 - 卷积(Locality + Stationarity of images,本地性 + 图像的平稳性):
卷积操作利用了图像的局部性,即图像中的相邻像素往往相关,因此可以通过局部的滤波器(卷积核)提取有意义的局部特征。同时,卷积操作也假设图像的统计特性在空间上是平稳的,即一个特征无论出现在图像的哪个部分,都具有相似的重要性。因此,卷积核在整个图像中共享,可以捕捉到相似的模式。 - 池化(Invariance of object class to translations,物体类别对平移的不变性):
池化操作通过减少特征图的空间尺寸,使得模型对物体在图像中的位置不敏感。这种不变性使得模型能够正确识别出被平移(即在图像中位置发生变化)的物体类别,从而增强了模型的鲁棒性和泛化能力。
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torchvision import datasets, transforms
import matplotlib.pyplot as plt
import numpy
# 一个函数,用来计算模型中有多少参数
def get_n_params(model):
np=0
for p in list(model.parameters()):
np += p.nelement()
return np
# 使用GPU训练
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
1. 加载数据 (MNIST)
PyTorch里包含了 MNIST, CIFAR10 等常用数据集,调用 torchvision.datasets 即可把这些数据由远程下载到本地,下面给出MNIST的使用方法:
torchvision.datasets.MNIST(root, train=True, transform=None, target_transform=None, download=False)
- root 为数据集下载到本地后的根目录,包括 training.pt 和 test.pt 文件
- train,如果设置为True,从training.pt创建数据集,否则从test.pt创建。
- download,如果设置为True, 从互联网下载数据并放到root文件夹下
- transform, 一种函数或变换,输入PIL图片,返回变换之后的数据。
- target_transform 一种函数或变换,输入目标,进行变换。
另外值得注意的是,DataLoader是一个比较重要的类,提供的常用操作有:batch_size(每个batch的大小), shuffle(是否进行随机打乱顺序的操作), num_workers(加载数据的时候使用几个子进程)
input_size = 28*28 # MNIST上的图像尺寸是 28x28
output_size = 10 # 类别为 0 到 9 的数字,因此为十类
# transforms.ToTensor():将PIL图像或numpy数组转换为PyTorch的张量(tensor),并将图像的像素值从[0, 255]归一化到[0.0, 1.0]。
# transforms.Normalize((0.1307,), (0.3081,)):对图像进行标准化处理,使用的均值是0.1307,标准差是0.3081。此均值和标准差是从MNIST训练数据中计算得出的。
train_loader = torch.utils.data.DataLoader(
datasets.MNIST('./data', train=True, download=True,
transform=transforms.Compose(
[transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))])),
batch_size=64, shuffle=True)
test_loader = torch.utils.data.DataLoader(
datasets.MNIST('./data', train=False, transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))])),
batch_size=1000, shuffle=True)
显示数据集中的部分图像
# 创建一个新的图形对象,并设置图形的大小为8x5英寸。这个尺寸决定了最终图像在显示或保存时的物理尺寸。
plt.figure(figsize=(8, 5))
# 绘制20张图片
for i in range(20):
# 创建一个4行5列的子图,并指定当前要绘制的子图位置为第 i + 1 个。
plt.subplot(4, 5, i + 1)
"""
image 是从数据集中获取的张量,形状为 [1, 28, 28],其中 1 表示通道数(灰度图像),28x28 是图像的大小。
"""
image, _ = train_loader.dataset.__getitem__(i)
"""
image.squeeze():将图像张量的维度从 [1, 28, 28] 压缩为 [28, 28],去除维度为1的通道维度。
.numpy():将张量转换为NumPy数组,以便 matplotlib 处理。
'gray':指定显示图像时使用灰度色彩映射。
"""
plt.imshow(image.squeeze().numpy(),'gray')
plt.axis('off');

2. 创建网络
定义网络时,需要继承nn.Module,并实现它的forward方法,把网络中具有可学习参数的层放在构造函数__init__中。
只要在nn.Module的子类中定义了forward函数,backward函数就会自动被实现(利用autograd)。
class FC2Layer(nn.Module):
'''
参数数量:
input_size = 28 * 28 = 784,n_hidden =8 ,output_size=10
第一层参数:784*8+8=6280
第二层参数:8*8+8=72
第三次参数:8*10+10=90
总参数个数:6442
'''
def __init__(self, input_size, n_hidden, output_size):
# nn.Module子类的函数必须在构造函数中执行父类的构造函数
# 下式等价于nn.Module.__init__(self)
super(FC2Layer, self).__init__()
self.input_size = input_size
# 这里直接用 Sequential 就定义了网络,注意要和下面 CNN 的代码区分开
self.network = nn.Sequential(
nn.Linear(input_size, n_hidden),
nn.ReLU(),
nn.Linear(n_hidden, n_hidden),
nn.ReLU(),
nn.Linear(n_hidden, output_size),
nn.LogSoftmax(dim=1)
)
def forward(self, x):
# view一般出现在model类的forward函数中,用于改变输入或输出的形状
# x.view(-1, self.input_size) 的意思是多维的数据展成二维
# 代码指定二维数据的列数为 input_size=784,行数 -1 表示我们不想算,电脑会自己计算对应的数字
# 在 DataLoader 部分,我们可以看到 batch_size 是64,所以得到 x 的行数是64
# 大家可以加一行代码:print(x.cpu().numpy().shape)
# 训练过程中,就会看到 (64, 784) 的输出,和我们的预期是一致的
# forward 函数的作用是,指定网络的运行过程,这个全连接网络可能看不啥意义,
# 下面的CNN网络可以看出 forward 的作用。
x = x.view(-1, self.input_size)
# x = x.reshape(-1, self.input_size)
return self.network(x)
class CNN(nn.Module):
'''
nput_size = 28 * 28 = 784,n_feature =6 ,output_size=10
第一层:conv1=150+6
第二层:max_pool2d
第三层:conv2=900+6
第四层:max_pool2d
第五层:fc1,该层的输入特征数量经过前四层依次变为了 1*28*28=784 -> 6*24*24=3456 -> 6*12*12=864 -> 6*8*8=256 -> 6*4*4=96
所以该层的参数量:96*50+50=4850
第六层:fc2,50*10+10=510
总参数为156+906+4850+510=6422
'''
def __init__(self, input_size, n_feature, output_size):
# 执行父类的构造函数,所有的网络都要这么写
super(CNN, self).__init__()
# 下面是网络里典型结构的一些定义,一般就是卷积和全连接
# 池化、ReLU一类的不用在这里定义
self.n_feature = n_feature
# 输入通道为1(适用于单通道灰度图像),输出通道为 n_feature(定义的特征数量),卷积核大小为 5x5。
self.conv1 = nn.Conv2d(in_channels=1, out_channels=n_feature, kernel_size=5)
self.conv2 = nn.Conv2d(n_feature, n_feature, kernel_size=5)
self.fc1 = nn.Linear(n_feature*4*4, 50)
self.fc2 = nn.Linear(50, 10)
# 下面的 forward 函数,定义了网络的结构,按照一定顺序,把上面构建的一些结构组织起来
# 意思就是,conv1, conv2 等等的,可以多次重用
def forward(self, x, verbose=False):
x = self.conv1(x)
x = F.relu(x)
x = F.max_pool2d(x, kernel_size=2)
x = self.conv2(x)
x = F.relu(x)
x = F.max_pool2d(x, kernel_size=2)
# x = x.view(-1, self.n_feature*4*4):将池化后的特征图展平为一维,以便传入全连接层。
# -1 表示自动推导批量大小,self.n_feature * 4 * 4 是展平后的特征向量大小。
x = x.view(-1, self.n_feature*4*4)
x = self.fc1(x)
x = F.relu(x)
x = self.fc2(x)
x = F.log_softmax(x, dim=1)
return x
定义训练和测试函数
# 训练函数
def train(model):
# 设置model为训练模式。某些层(如Dropout和BatchNorm)在训练和测试模式下的行为有所不同,因此在训练时需要调用此方法以确保模型的行为正确。
model.train()
"""
enumerate(train_loader):遍历训练数据加载器 train_loader,每次迭代返回一个批次的数据和目标标签。
batch_idx 是当前批次的索引, (data, target) 是批次中的数据和标签。
"""
for batch_idx, (data, target) in enumerate(train_loader):
# 把数据送到GPU中
data, target = data.to(device), target.to(device)
optimizer.zero_grad()
output = model(data)
# 计算负对数似然损失(negative log-likelihood loss),通常用于分类任务。
loss = F.nll_loss(output, target)
# 方向传播计算梯度
loss.backward()
# 更新参数
optimizer.step()
if batch_idx % 100 == 0:
print('Train: [{}/{} ({:.0f}%)]\tLoss: {:.6f}'.format(
batch_idx * len(data), len(train_loader.dataset),
100. * batch_idx / len(train_loader), loss.item()))
def test(model):
# 将模型设置为评估模式
model.eval()
test_loss = 0
correct = 0
for data, target in test_loader:
# 把数据送到GPU中
data, target = data.to(device), target.to(device)
# 把数据送入模型,得到预测结果
output = model(data)
# 计算本次batch的损失,并加到 test_loss 中
test_loss += F.nll_loss(output, target, reduction='sum').item()
# get the index of the max log-probability,最后一层输出10个数,
# 值最大的那个即对应着分类结果,然后把分类结果保存在 pred 里
"""
.max(1, keepdim=True):在类别维度(1)上找到最大值及其索引。keepdim=True 确保输出张量的维度保持不变。
[1]:选择最大值的索引,这就是预测的类别标签。
"""
pred = output.data.max(1, keepdim=True)[1]
# 将 pred 与 target 相比,得到正确预测结果的数量,并加到 correct 中
# 这里需要注意一下 view_as ,意思是把 target 变成维度和 pred 一样的意思
correct += pred.eq(target.data.view_as(pred)).cpu().sum().item()
test_loss /= len(test_loader.dataset)
accuracy = 100. * correct / len(test_loader.dataset)
print('\nTest set: Average loss: {:.4f}, Accuracy: {}/{} ({:.0f}%)\n'.format(
test_loss, correct, len(test_loader.dataset),
accuracy))
3. 在小型全连接网络上训练(Fully-connected network)
n_hidden = 8 # number of hidden units
model_fnn = FC2Layer(input_size, n_hidden, output_size)
model_fnn.to(device)
optimizer = optim.SGD(model_fnn.parameters(), lr=0.01, momentum=0.5)
print('Number of parameters: {}'.format(get_n_params(model_fnn)))
train(model_fnn)
test(model_fnn)
Number of parameters: 6442
Train: [0/60000 (0%)] Loss: 2.447731
Train: [6400/60000 (11%)] Loss: 1.787504
Train: [12800/60000 (21%)] Loss: 1.327380
Train: [19200/60000 (32%)] Loss: 0.817053
Train: [25600/60000 (43%)] Loss: 0.774302
Train: [32000/60000 (53%)] Loss: 0.769718
Train: [38400/60000 (64%)] Loss: 0.663008
Train: [44800/60000 (75%)] Loss: 0.713497
Train: [51200/60000 (85%)] Loss: 0.326436
Train: [57600/60000 (96%)] Loss: 0.564632
Test set: Average loss: 0.4205, Accuracy: 8788/10000 (88%)
3. 在卷积神经网络上训练
需要注意的是,上在定义的CNN和全连接网络,拥有相同数量的模型参数
# Training settings
n_features = 6 # number of feature maps
model_cnn = CNN(input_size, n_features, output_size)
model_cnn.to(device)
optimizer = optim.SGD(model_cnn.parameters(), lr=0.01, momentum=0.5)
print('Number of parameters: {}'.format(get_n_params(model_cnn)))
train(model_cnn)
test(model_cnn)
Number of parameters: 6422
Train: [0/60000 (0%)] Loss: 2.310429
C:\Users\Joker\.conda\envs\pytorch\Lib\site-packages\torch\nn\modules\conv.py:456: UserWarning: Plan failed with a cudnnException: CUDNN_BACKEND_EXECUTION_PLAN_DESCRIPTOR: cudnnFinalize Descriptor Failed cudnn_status: CUDNN_STATUS_NOT_SUPPORTED (Triggered internally at C:\cb\pytorch_1000000000000\work\aten\src\ATen\native\cudnn\Conv_v8.cpp:919.)
return F.conv2d(input, weight, bias, self.stride,
C:\Users\Joker\.conda\envs\pytorch\Lib\site-packages\torch\autograd\graph.py:744: UserWarning: Plan failed with a cudnnException: CUDNN_BACKEND_EXECUTION_PLAN_DESCRIPTOR: cudnnFinalize Descriptor Failed cudnn_status: CUDNN_STATUS_NOT_SUPPORTED (Triggered internally at C:\cb\pytorch_1000000000000\work\aten\src\ATen\native\cudnn\Conv_v8.cpp:919.)
return Variable._execution_engine.run_backward( # Calls into the C++ engine to run the backward pass
Train: [6400/60000 (11%)] Loss: 1.943792
Train: [12800/60000 (21%)] Loss: 0.358685
Train: [19200/60000 (32%)] Loss: 0.366543
Train: [25600/60000 (43%)] Loss: 0.492693
Train: [32000/60000 (53%)] Loss: 0.096839
Train: [38400/60000 (64%)] Loss: 0.086685
Train: [44800/60000 (75%)] Loss: 0.194051
Train: [51200/60000 (85%)] Loss: 0.096391
Train: [57600/60000 (96%)] Loss: 0.097376
Test set: Average loss: 0.1357, Accuracy: 9579/10000 (96%)
通过上面的测试结果,可以发现,含有相同参数的 CNN 效果要明显优于 简单的全连接网络,是因为 CNN 能够更好的挖掘图像中的信息,主要通过两个手段:
- 卷积:Locality and stationarity in images
- 池化:Builds in some translation invariance
5. 打乱像素顺序再次在两个网络上训练与测试
考虑到CNN在卷积与池化上的优良特性,如果我们把图像中的像素打乱顺序,这样 卷积 和 池化 就难以发挥作用了,为了验证这个想法,我们把图像中的像素打乱顺序再试试。
首先下面代码展示随机打乱像素顺序后,图像的形态:
# 这里解释一下 torch.randperm 函数,给定参数n,返回一个从0到n-1的随机整数排列
perm = torch.randperm(784)
plt.figure(figsize=(8, 4))
for i in range(10):
image, _ = train_loader.dataset.__getitem__(i)
# permute pixels
"""
image.view(-1, 28*28):将图像展平为一维向量(大小为784),准备进行像素重新排列。
.clone():创建一个图像的副本,以免直接修改原图像数据。
image_perm[:, perm]:根据 perm 中的随机顺序重新排列图像的像素。
image_perm.view(-1, 1, 28, 28):将重新排列后的图像重新形成为 28x28 的图像。
"""
image_perm = image.view(-1, 28*28).clone()
image_perm = image_perm[:, perm]
image_perm = image_perm.view(-1, 1, 28, 28)
plt.subplot(4, 5, i + 1)
plt.imshow(image.squeeze().numpy(), 'gray')
plt.axis('off')
plt.subplot(4, 5, i + 11)
plt.imshow(image_perm.squeeze().numpy(), 'gray')
plt.axis('off')

重新定义训练与测试函数,我们写了两个函数 train_perm 和 test_perm,分别对应着加入像素打乱顺序的训练函数与测试函数。
与之前的训练与测试函数基本上完全相同,只是对 data 加入了打乱顺序操作。
# 对每个 batch 里的数据,打乱像素顺序的函数
def perm_pixel(data, perm):
# 转化为二维矩阵
data_new = data.view(-1, 28*28)
# 打乱像素顺序
data_new = data_new[:, perm]
# 恢复为原来4维的 tensor
data_new = data_new.view(-1, 1, 28, 28)
return data_new
# 训练函数
def train_perm(model, perm):
model.train()
for batch_idx, (data, target) in enumerate(train_loader):
data, target = data.to(device), target.to(device)
# 像素打乱顺序
data = perm_pixel(data, perm)
optimizer.zero_grad()
output = model(data)
loss = F.nll_loss(output, target)
loss.backward()
optimizer.step()
if batch_idx % 100 == 0:
print('Train: [{}/{} ({:.0f}%)]\tLoss: {:.6f}'.format(
batch_idx * len(data), len(train_loader.dataset),
100. * batch_idx / len(train_loader), loss.item()))
# 测试函数
def test_perm(model, perm):
model.eval()
test_loss = 0
correct = 0
for data, target in test_loader:
data, target = data.to(device), target.to(device)
# 像素打乱顺序
data = perm_pixel(data, perm)
output = model(data)
test_loss += F.nll_loss(output, target, reduction='sum').item()
pred = output.data.max(1, keepdim=True)[1]
correct += pred.eq(target.data.view_as(pred)).cpu().sum().item()
test_loss /= len(test_loader.dataset)
accuracy = 100. * correct / len(test_loader.dataset)
print('\nTest set: Average loss: {:.4f}, Accuracy: {}/{} ({:.0f}%)\n'.format(
test_loss, correct, len(test_loader.dataset),
accuracy))
在全连接网络上训练与测试:
perm = torch.randperm(784)
n_hidden = 8 # number of hidden units
model_fnn = FC2Layer(input_size, n_hidden, output_size)
model_fnn.to(device)
optimizer = optim.SGD(model_fnn.parameters(), lr=0.01, momentum=0.5)
print('Number of parameters: {}'.format(get_n_params(model_fnn)))
train_perm(model_fnn, perm)
test_perm(model_fnn, perm)
Number of parameters: 6442
Train: [0/60000 (0%)] Loss: 2.359195
Train: [6400/60000 (11%)] Loss: 1.950317
Train: [12800/60000 (21%)] Loss: 1.554770
Train: [19200/60000 (32%)] Loss: 1.118916
Train: [25600/60000 (43%)] Loss: 0.862258
Train: [32000/60000 (53%)] Loss: 0.771859
Train: [38400/60000 (64%)] Loss: 0.420492
Train: [44800/60000 (75%)] Loss: 0.553502
Train: [51200/60000 (85%)] Loss: 0.524959
Train: [57600/60000 (96%)] Loss: 0.550625
Test set: Average loss: 0.5138, Accuracy: 8454/10000 (85%)
在卷积神经网络上训练与测试:
perm = torch.randperm(784)
n_features = 6 # number of feature maps
model_cnn = CNN(input_size, n_features, output_size)
model_cnn.to(device)
optimizer = optim.SGD(model_cnn.parameters(), lr=0.01, momentum=0.5)
print('Number of parameters: {}'.format(get_n_params(model_cnn)))
train_perm(model_cnn, perm)
test_perm(model_cnn, perm)
Number of parameters: 6422
Train: [0/60000 (0%)] Loss: 2.294312
Train: [6400/60000 (11%)] Loss: 2.265878
Train: [12800/60000 (21%)] Loss: 2.252986
Train: [19200/60000 (32%)] Loss: 2.101082
Train: [25600/60000 (43%)] Loss: 1.784680
Train: [32000/60000 (53%)] Loss: 1.304697
Train: [38400/60000 (64%)] Loss: 0.977341
Train: [44800/60000 (75%)] Loss: 0.788397
Train: [51200/60000 (85%)] Loss: 0.847415
Train: [57600/60000 (96%)] Loss: 0.673661
Test set: Average loss: 0.6098, Accuracy: 8039/10000 (80%)
从打乱像素顺序的实验结果来看,全连接网络的性能基本上没有发生变化,但是 卷积神经网络的性能明显下降。
这是因为对于卷积神经网络,会利用像素的局部关系,但是打乱顺序以后,这些像素间的关系将无法得到利用。