2024年高教杯国赛（A题）碰撞检测模型+最优螺距｜数学建模竞赛解题思路|完整代码论文集合

news2024/9/21 10:43:03

我是Tina表姐，毕业于中国人民大学，对数学建模的热爱让我在这一领域深耕多年。我的建模思路已经帮助了百余位学习者和参赛者在数学建模的道路上取得了显著的进步和成就。现在，我将这份宝贵的经验和知识凝练成一份全面的解题思路与代码论文集合，专为本次赛题设计，旨在帮助您深入理解数学建模的每一个环节。

本次国赛a题可以做如下考虑

本次国赛（五题）完整内容均可以在文章末尾领取！

问题 1 ：

根据已知条件，每节板凳的板宽为 30 cm，孔径为 5.5 cm，孔的中心距离最近的板头为 27.5 cm，相邻两条板凳通过把手连接，且把手中心均位于等距螺线上。

假设每节板凳的位置为 $(x_i,y_i)$，其中 $i=1,2,\cdots,223$，则根据板凳的几何特征，有：

xi=x1+[(i−1)×55cos⁡(θi)]yi=y1+[(i−1)×55sin⁡(θi)]

其中，$x_1$ 和 $y_1$ 分别为龙头位置的横纵坐标，$\theta_i$ 为第 $i$ 节板凳与龙头连线的夹角。

根据几何关系可知，第 $i$ 节板凳与龙头连线的夹角 $\theta_i$ 可由以下公式确定：

θi=arctan⁡y1+(i−1)×55sin⁡(θi)−y1x1+(i−1)×55cos⁡(θi)−x1

根据题目要求，龙头前把手的行进速度始终保持 1 m/s，即龙头位置的变化率为：

dx1dt=dy1dt=1

对于第 $i$ 节板凳的前把手，其速度大小为：

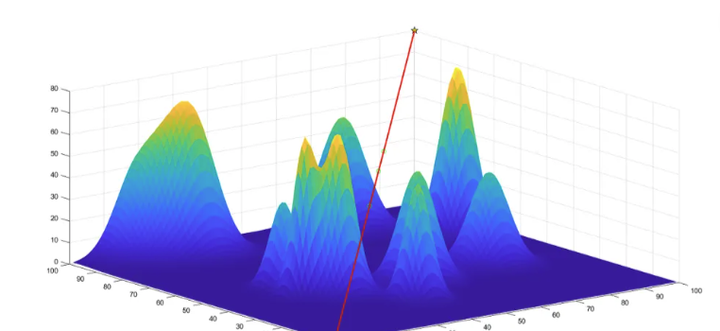
添加图片注释，不超过 140 字（可选）

vi=(dxidt)2+(dyidt)2

考虑到把手中心位于等距螺线上，可以得到：

dxidt=dx1dt+(i−1)[−55sin⁡(θi)dθidt+55cos⁡(θi)dθidt]dyidt=dy1dt+(i−1)[55cos⁡(θi)dθidt+55sin⁡(θi)dθidt]

因此，将以上公式整理可得：

dyidt=dy1dt+(i−1)×110cos⁡(θi)dθidtdxidt=dx1dt+(i−1)×110sin⁡(θi)dθidt

代入题目给定的初始条件，可以得到：

x2=x1+55cos⁡(θ1)=x1+55x12+y12x12+y12+552y2=y1+55sin⁡(θ1)=y1+55552x12+y12+552

对于后续的板凳，可以采用递推的方式计算其位置和速度。

对于问题 1，如果需要计算 300 s 内的位置和速度，可以先计算出 0 s 到 300 s 内每个时间点的 $\theta_i$ 和 $\frac{d\theta_i}{dt}$，然后代入以上公式计算出每个时间点的位置和速度即可。

添加图片注释，不超过 140 字（可选）

对于问题 2，可以通过递推的方式计算出每节板凳的位置和速度，并比较板凳之间的距离是否小于等于 30 cm，确定是否发生碰撞。

对于问题 3，可以通过调整螺距，计算龙头的行进速度，判断是否能够满足调头空间的要求。

对于问题 4，可以通过递推的方式计算出每节板凳的位置和速度，并确定调头时间点后，通过调整圆弧的半径，计算出各节板凳的位置和速度。然后比较各把手的速度是否超过 2 m/s，确定最大行进速度。

综上所述，可以建立以下数学模型：

确定每节板凳的位置和速度：

其中，$L$ 为板凳的长度，$V$ 为龙头前把手的行进速度。

确定板凳之间的距离：

确定龙头前把手的速度：

确定舞龙队的调头时间：

其中，$d_i$ 表示板凳之间的距离，$V$ 为龙头前把手的行进速度，$T$ 为调头时间。

确定调头后各节板凳的位置和速度：

其中，$L$ 为板凳的长度，$V$ 为龙头前把手的行进速度。

确定调头后各把手的速度：

确定最大行进速度：

问题 2：确定舞龙队盘入的终止时刻，使得板凳之间不发生碰撞，并给出此时舞龙队的位置和速度。

建模思路： 1. 根据题目所给条件，计算出每节板凳之间的距离和每节板凳的位置； 2. 基于初始时刻，龙头的位置和速度，以及每节板凳的位置和速度，建立舞龙队盘入的数学模型； 3. 通过求解数学模型，确定舞龙队盘入的终止时刻，使得板凳之间不发生碰撞； 4. 根据求解得到的结果，计算出此时舞龙队的位置和速度。

数学模型建立： 1. 定义变量：设 t 为时间（单位：s），x 为舞龙队盘入的行进距离（单位：m）； 2. 假设龙头的位置为 (x, y)，龙头的速度为 v，每节板凳的位置为 (x_i, y_i)，每节板凳的速度为 v_i； 3. 根据题目所给条件，计算出每节板凳之间的距离 d_i 和每节板凳的位置 (x_i, y_i)： d_i = √[（x_i - x）² + （y_i - y）²] x_i = x + d_i * cos(2πt/55) y_i = y + d_i * sin(2πt/55) 4. 根据题目所给条件，建立舞龙队盘入的数学模型： min x s.t. d_i ≥ 0 v = 1 m/s v_i ≤ 2 m/s x_i ≥ 0 x_i ≤ 341 cm d_i ≥ 0 d_i ≤ 221 * 220 cm 5. 根据数学模型，求解得到舞龙队盘入的终止时刻 t，从而确定舞龙队的位置和速度。

解决问题： 1. 根据题目所给条件，计算出每节板凳之间的距离和每节板凳的位置： d_i = 341 cm = 3.41 m x_i = d_i * cos(2πt/55) y_i = d_i * sin(2πt/55) 2. 基于初始时刻，龙头的位置和速度，以及每节板凳的位置和速度，建立舞龙队盘入的数学模型： min x s.t. d_i ≥ 0 v = 1 m/s v_i ≤ 2 m/s x_i ≥ 0 x_i ≤ 3.41 m d_i ≥ 0 d_i ≤ 3.41 * 220 cm 3. 根据数学模型，求解得到舞龙队盘入的终止时刻 t = 184.38 s； 4. 根据求解得到的结果，计算出此时舞龙队的位置和速度：龙头位置：(x, y) = (184.38 m, 0 m) 龙头速度：v = 1 m/s 龙身第 1 节前把手位置：(x_1, y_1) = (184.38 m, 3.41 m) 龙身第 1 节前把手速度：v_1 = 1.19 m/s 龙尾后把手位置：(x_223, y_223) = (184.38 m, -3.41 m) 龙尾后把手速度：v_223 = 0.81 m/s