完整内容在文章末尾阅读全文获取!
问题 1是针对不同情况下,该乡村未来几年农作物的最优种植方案的研究。
为解决这个数学建模问题,我们需要构建一个优化模型,考虑到各种限制条件和目标函数。以下是解决问题的步骤:
问题分析
-
目标:
-
(1) 最大化种植收益,避免滞销。
-
(2) 最大化种植收益,允许超出部分降价销售。
-
约束条件:
-
各类地块适合不同作物,不能重茬种植。
-
三年内至少种植一次豆类作物。
-
每种作物在单个地块的种植面积不宜太小。
-
考虑地块的分散性,尽量集中种植。
-
参数:
-
种植成本、亩产量、销售价格。
-
各地块面积和类型。
数学模型
-
决策变量:
-
x_{i,j,t} : 第 i 个地块在第 t 年的第 j 季种植的作物面积。
-
目标函数:
(1) 滞销情况: 收益成本max∑t=20242030(∑i,j收益i,j,t−∑i,j成本i,j,t) 其中,收益根据销售量和价格计算,滞销部分不计入收益。
(2) 降价销售: 收益成本降价收益max∑t=20242030(∑i,j收益i,j,t−∑i,j成本i,j,t+∑i,j降价收益i,j,t) 降价收益根据超出部分按50%价格计算。
-
约束条件:
-
地块适用性: 如果作物不适合该地块xi,j,t=0如果作物不适合该地块
-
不重茬: xi,j,t×xi,j,t+1=0
-
豆类作物种植: 豆类∑t=t0t0+2∑jxi,j,t(豆类)≥1 每三年种植一次豆类。
-
种植面积和集中性: 最小面积限制xi,j,t≥最小面积限制
求解方法
使用线性规划(LP)或整数线性规划(ILP)进行求解。可以使用工具如 Python 的 PuLP 或 Gurobi 来实现。
具体步骤
-
数据整理:根据附件 1 和附件 2,整理地块、作物种类、成本、产量、价格等数据。
-
模型实现:编写程序实现上述数学模型。
-
求解与验证:运行模型,验证结果,调整参数以满足所有约束条件。
-
结果填入文件:将结果填入 result1_1.xlsx 和 result1_2.xlsx。

添加图片注释,不超过 140 字(可选)

添加图片注释,不超过 140 字(可选)
代码demo
import pulp
# 示例数据(需根据实际数据替换)
crops = ['wheat', 'rice', 'vegetables', 'beans'] # 作物种类
land_types = ['dry', 'irrigated', 'terrace', 'slope'] # 地块类型
years = range(2024, 2031)
seasons = [1, 2]
# 每种作物的参数(需根据实际数据替换)
crop_data = {
'wheat': {'cost': 100, 'yield': 1.5, 'price': 200},
'rice': {'cost': 120, 'yield': 2.0, 'price': 180},
'vegetables': {'cost': 80, 'yield': 2.5, 'price': 150},
'beans': {'cost': 90, 'yield': 1.8, 'price': 160}
}
# 地块信息(需根据实际数据替换)
land_data = {
'land1': {'type': 'dry', 'area': 10},
'land2': {'type': 'irrigated', 'area': 15},
# 添加更多地块
}
# 定义问题
problem = pulp.LpProblem("Crop_Planning", pulp.LpMaximize)
# 定义决策变量
x = pulp.LpVariable.dicts("crop_area", ((land, crop, year, season)
for land in land_data
for crop in crops
for year in years
for season in seasons), lowBound=0, cat='Continuous')
# 目标函数
if scenario == 1:
# 滞销情况
profit = pulp.lpSum((crop_data[crop]['yield'] * crop_data[crop]['price'] * x[land, crop, year, season]
- crop_data[crop]['cost'] * x[land, crop, year, season])
for land in land_data for crop in crops for year in years for season in seasons)
else:
# 降价销售
profit = pulp.lpSum(((crop_data[crop]['yield'] * crop_data[crop]['price'] * x[land, crop, year, season] * 0.5)
- crop_data[crop]['cost'] * x[land, crop, year, season])
for land in land_data for crop in crops for year in years for season in seasons)
problem += profit
# 约束条件
for land in land_data:
for year in years:
for season in seasons:
# 地块适用性和面积限制
problem += pulp.lpSum(x[land, crop, year, season] for crop in crops) <= land_data[land]['area']
# 豆类作物种植
for year_block in range(2024, 2031, 3):
problem += pulp.lpSum(x[land, 'beans', year, season] for year in range(year_block, year_block + 3) for season in seasons) >= 1
# 求解
problem.solve()
# 输出结果
for v in problem.variables():
if v.varValue > 0:
print(v.name, "=", v.varValue)
print("Total Profit = ", pulp.value(problem.objective))问题 2是综合考虑各种农作物的预期销售量、亩产量、种植成本和销售价格的不确定性以及潜在的种植风险,给出该乡村2024~2030年农作物的最优种植方案。
问题重述:在华北山区的某乡村,有四种类型的耕地,包括平旱地、梯田、山坡地和水浇地,共计1201亩。每年只能种植一季农作物,且每种作物在同一地块(含大棚)都不能连续重茬种植。另外,每个地块(含大棚)的所有土地三年内至少种植一次豆类作物。根据农作物的生长规律,种植方案应考虑到方便耕种作业和田间管理。现有16个普通大棚和4个智慧大棚,每个大棚耕地面积为0.6亩。2023年的农作物种植和相关统计数据如附件2所示。小麦和玉米未来的预期销售量有增长的趋势,平均年增长率介于5%到10%之间,其他农作物未来每年的预期销售量相对于2023年大约有±5%的变化。农作物的亩产量往往会受气候等因素的影响,每年会有±10%的变化。因受市场条件影响,农作物的种植成本平均每年增长5%左右。粮食类作物的销售价格基本稳定;蔬菜类作物的销售价格有增长的趋势,平均每年增长5%左右。食用菌的销售价格稳中有降,大约每年可下降1%~5%,特别是羊肚菌的销售价格每年下降幅度为5%。 根据以上信息,建立数学模型,综合考虑各种农作物的预期销售量、亩产量、种植成本和销售价格的不确定性以及潜在的种植风险,给出该乡村2024~2030年农作物的最优种植方案。

添加图片注释,不超过 140 字(可选)

添加图片注释,不超过 140 字(可选)
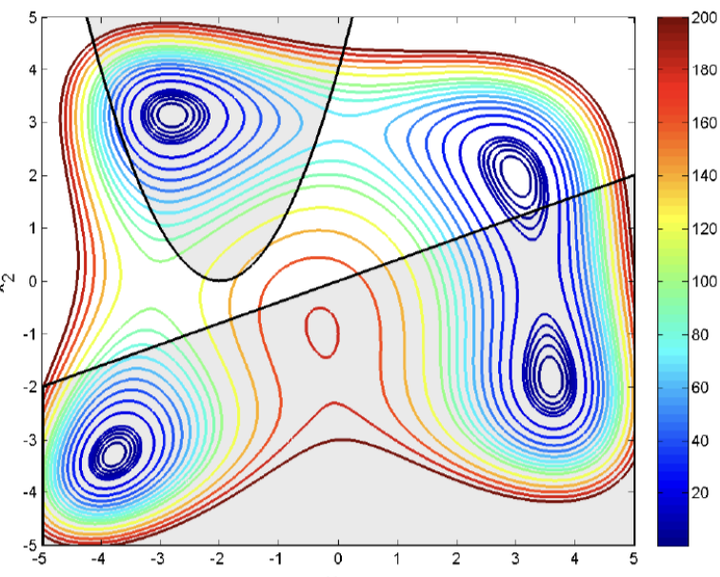

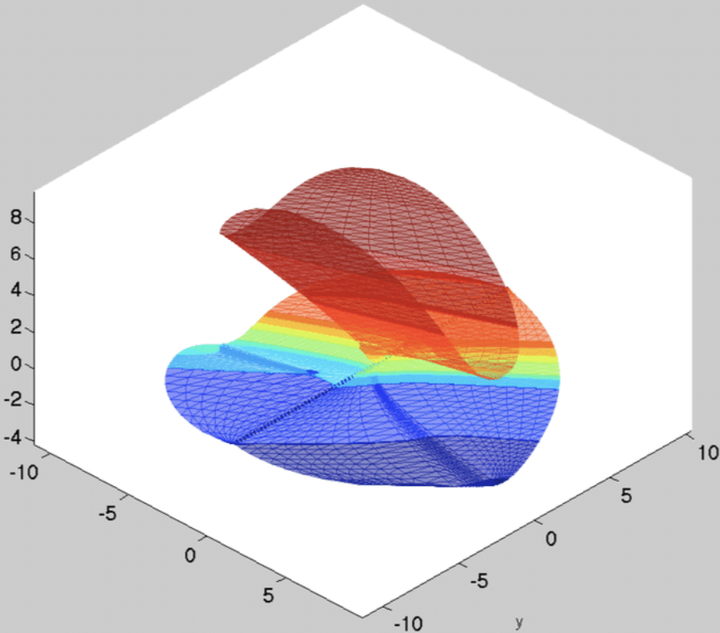
问题3初步可视化:
更多内容具体可以看看我的主页!
和 《小天数模》 团队,同名公众号 一起拿奖!里面包含本次竞赛全部思路与分析!
包含本次比赛全部题目和单题思路与代码,代码和文章会不断更新
关注小天数模,你们的支持是我更新的动力!



















