2024-9-5,星期四,20:40,天气:晴,心情:晴。明天终于又要放假啦!继续学习。、
今天继续学习第九章,主要学习内容为:有源低通/高通滤波器(一阶滤波器+Sallen-Key滤波器+高下降率滤波器)+有源带通滤波器(级联+多重反馈+状态可变)。
一、有源滤波器(续)
1. 有源低通滤波器
与无源滤波器(仅含R、L。C的电路)相比,有源滤波器(运算放大器作为有源元件)有以下几点优势:
-
运算放大器可以提供增益,使得信号穿过滤波器时不会衰减;
-
运算放大器的高输入阻抗可以防止过度增加电源的负载;
-
运算放大器的低输入阻抗防止滤波器被负载影响;
-
很容易在很宽的频率范围内调整而不会改变所期望的响应、
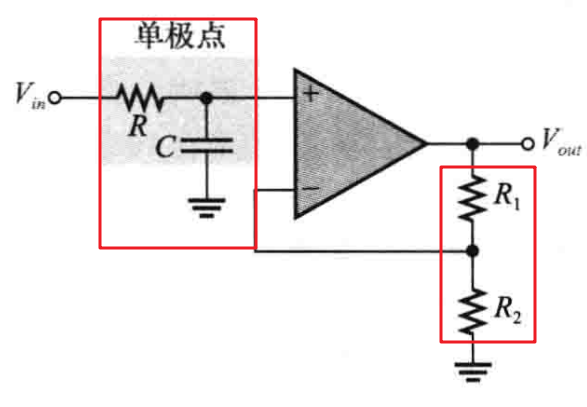
(1)一阶(单极点)滤波器:下图为一个含有单极点的一阶低通RC网络的有源滤波器
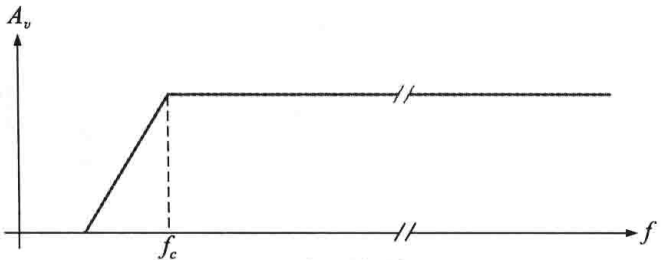
其响应曲线如下图所示,当大于截止频率时其下降率为-20dB/十倍频程:
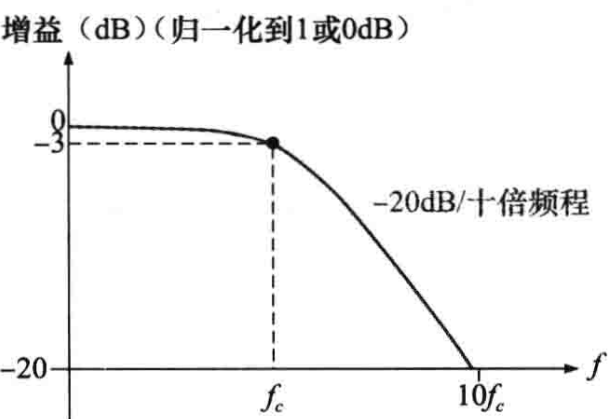
一阶滤波器的截止频率为fc = 1 / 2ΠRC,滤波器中的放大器为同相放大器,通带内的闭环电压增益由反馈分压电阻R1和R2决定:Acl(NI) = (R1 / R2) + 1。
(2)Sallen-Key滤波器:Sallen-Key是一种最常见的二阶(两极点)滤波器,通常也称为VCVS滤波器(电压控制的电压源),如下图所示:
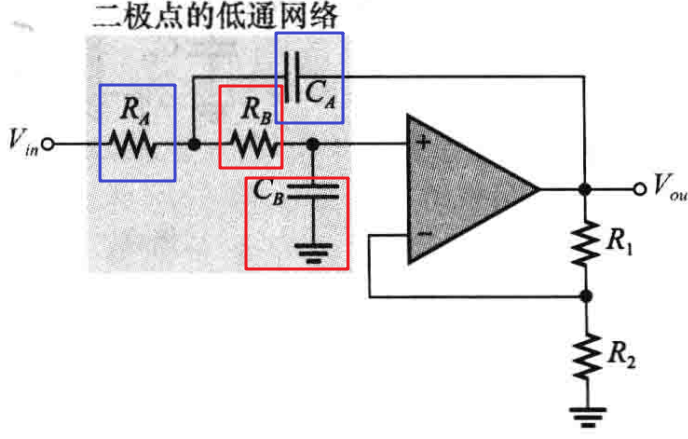
如上图所示,一个Sallen-Key低通滤波器有两个低通RC网络,当大于截止频率时其下降率为-40dB/十倍频程,其中,一个RC网络由RA和CA组成;另一个RC网络由RB和CB组成,该滤波器的一个重要特性是,由电容CA提供反馈,在接近通带边缘附近可以调整响应,二阶Sallen-Key滤波器的截止频率为fc = 1 / 2Π·(RACARBCB)1/2。当RA = RB = R且CA = CB = C时,截止频率为fc = 1 / 2ΠRC。与单极点滤波器相同,二阶Sallen-Key滤波器中的运算放大器是同相输入的,反馈网络由R1和R2构成,通过改变反馈电阻的值可以改变阻尼系数,从而使滤波器的响应呈现巴特沃斯、切比雪夫或贝塞尔响应中的任意一种。
(3)获得高下降率滤波器:上面讲到,如果想获得一个三级点滤波器,可以将一阶滤波器与二阶滤波器级联进行实现,如下图所示:
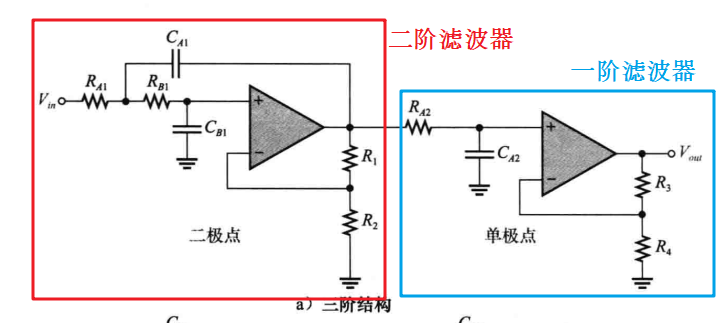
同理,如果需要一个四阶滤波器,则只需要将两个二阶滤波器级联即可:
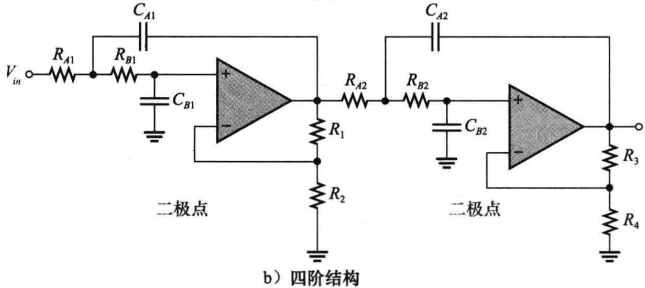
2. 有源高通滤波器
对于有源高通滤波器,除了电容的作用与有源低通滤波器相反外,其余参数均与有源低通滤波器相同。
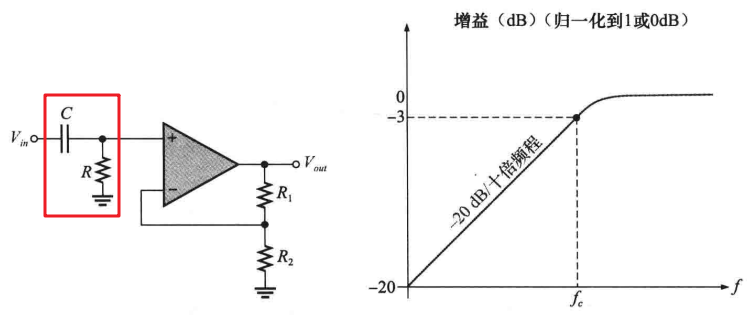
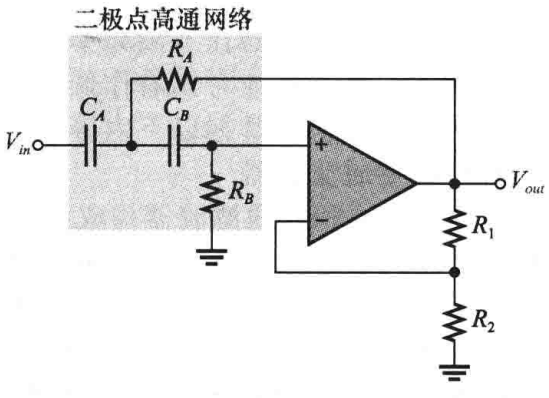
(1)一阶(单极点)滤波器:下图为一个典型的有源一阶高通滤波器,下降率为-20dB/十倍频程,反馈电路连接方法与一阶低通滤波器相同:
理想情况下,高通滤波器可以让所有频率大于截止频率fc的信号通过而不受任何限制:
但是通过之前的学习我们知道,组成高通率波其的RC网络在高频率处的响应会被限制,所以实际过程中对高通滤波器有上限频率的限制,即事实上高通滤波器其实为一个通带很大的带通滤波器:

而在大多数应用中,因为内部高频限制比滤波器的fc要大很多,所以可以忽略不计,在一些特殊的应用中,可以采用分立式晶体管或电流反馈运算器来作为增益原件而不是使用普通放大器,以达到增加上线频率的作用。
(2)Sallen-Key高通滤波器:下图为一个二阶高通Sallen-Key滤波器,从图中可以看到,除RC网络中的电容和电阻位置相反外,其余结构与低通滤波器相同,截止频率也与低通滤波器相同:
(3)级联高通滤波器:与低通滤波器完全相同,可以通过级联二阶与一阶高通滤波器组成告诫滤波器。
3. 有源带通滤波器
(1)级联低通&高通滤波器构成带通滤波器:构成带通滤波器的一种方法就是将低通滤波器与高通滤波器进行级联,如下图所示:
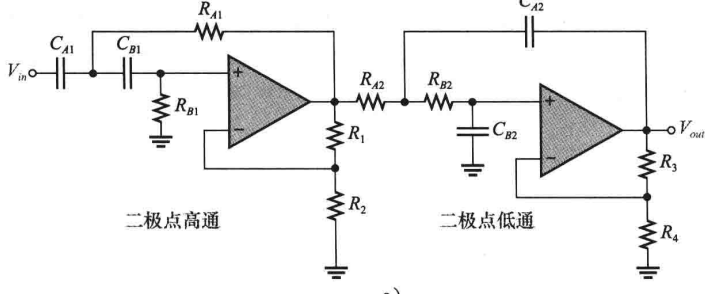
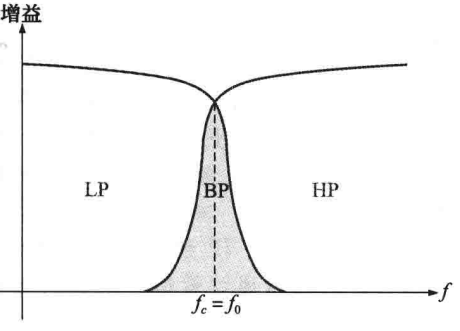
只要两个滤波器的截止频率有明显差异,且每个滤波器都是巴特沃斯结构,就可以合成一个带通响应曲线,如下图所示(每个滤波器都是二阶Sallen-Key结构,下降率为-40dB/十倍频程):
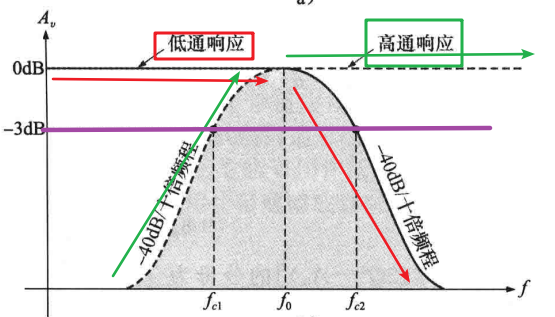
从图中可以看出,合理的选择每个滤波器的截止频率可以式响应曲线充分重叠,而且高通滤波器的截止频率必须比低通滤波器的截止频率低。综上所述,二阶带通滤波器的下限频率是高通滤波器的截止频率,上限频率是低通滤波器的截止频率,中心频率是上限频率与下限频率的几何均值,即:
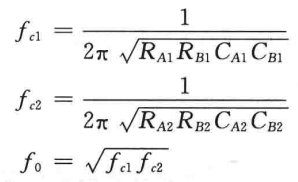
(2)多重反馈带通滤波器:如下图所示,该滤波器具有R2和C1两条反馈路径,R1和C1提供低通响应,R2和C2提供高通响应,中心频率处增益最大:
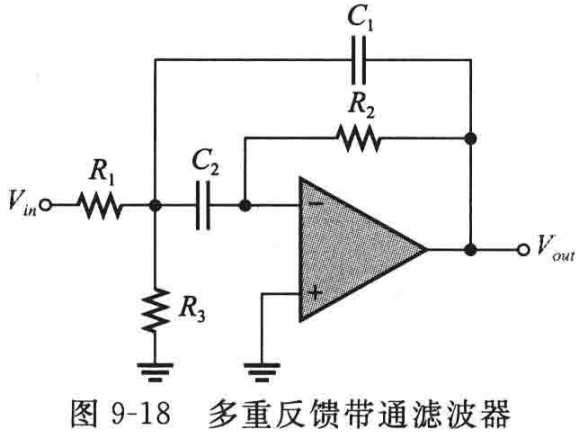
这种类型的滤波器Q一般小于10。从C1反馈路径看,R1和R3并联,中心频率可以表示为f0 = 1 / (2Π·((R1 || R3)R2C1C2)1/2),令C1 = C2 = C,可得中心频率f0为:
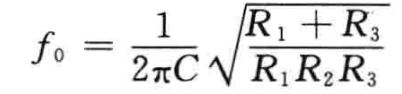
因为Q = f / BW,所以根据选定的C,f0,BW(fc2 = fc1)和A0可以确定需要的电阻阻值:
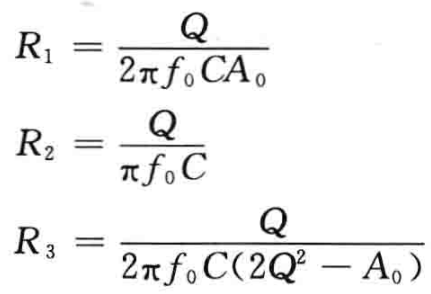
从R1和R2的表达式中可以分别得到功率因数Q的表达式:
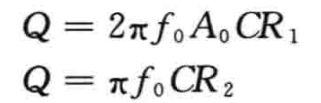
令2Πf0A0CR1 = Πf0CR2,可解得中心频率处的最大增益为A0 = R2 / (2R1),此外,为了使R3的分母为正,需要使A0 > 2Q2,这意味着增益系数将会受到限制。
(3)状态可变带通滤波器:状态可变带通滤波器由一个求和放大器和两个用作一阶低通滤波器的积分器通过级联的方式构成,中心频率由两个积分器的RC网络确定,当其作为带通滤波器的时(也可以作为低通/高通滤波器),通常把积分器的截止频率设置为相同,这样同时得到了中心频率。
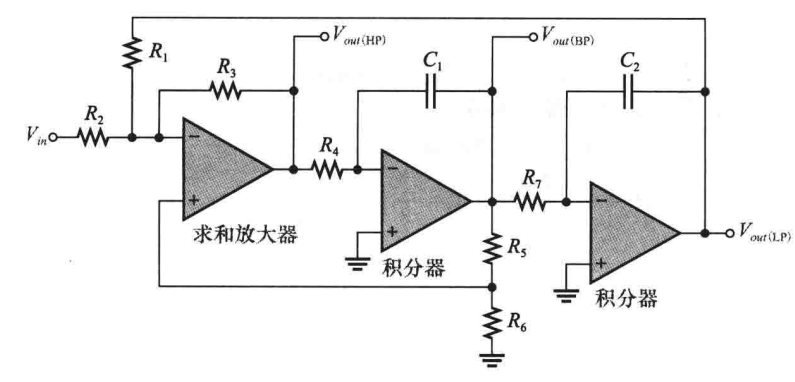
-
基本工作原理:当输入端频率低于fc时,输入信号通过求和放大器和积分器,并且在积分器的输出信号处以180°相位进行反馈,因此,对于所有低于fc的频率信号,反馈信号和输入信号相互抵消,随着低通响应的下降,反馈信号减小,允许输入信号通过通带输出,当频率高于fc时,低通响应逐渐小时,阻止输入信号通过积分器,所以,带通输出在fc处达到最大值,如下图所示:
这种类型的滤波器可以得到0~100范围内的任意稳定Q值,Q值由反馈电阻R5和R6决定,即:Q = 1/3((R5 / R6) + 1)。




















