目录
一、dfs基础
二、模板题
题目:98. 所有可达路径
题目链接
题解:dfs+邻接矩阵
三、小结
一、dfs基础
dfs是按照一个方向搜索到尽头再搜索其他方向。怎样实现对其他方向的搜索呢?我们可以通过回溯,撤销最后一步,再选择其他路线。 -- 回溯过程某种程度上也是递归的体现。所以,实现 dfs 的一个关键就是递归。
之前有了回溯的基础,其实可以发现回溯算法其实就是依靠 dfs 来实现。
这样我们就能得出 dfs 函数的基本模板(参考代码随想录):
void dfs(参数) {
if (终止条件) {
存放结果;
return;
}
for (选择:本节点所连接的其他节点) {
处理节点;
dfs(图,选择的节点); // 递归
回溯,撤销处理结果
}
}对于得到不同路径的问题,我们一般会采用两个数组来记录,一个存放所有路径,一个存放当前遍历的路径。
vector<vector<int>> ans; // 符合条件的所有路径
vector<int> path; // 当前遍历的路径二、模板题
题目:98. 所有可达路径
题目链接
98. 所有可达路径 (kamacoder.com)
题目描述
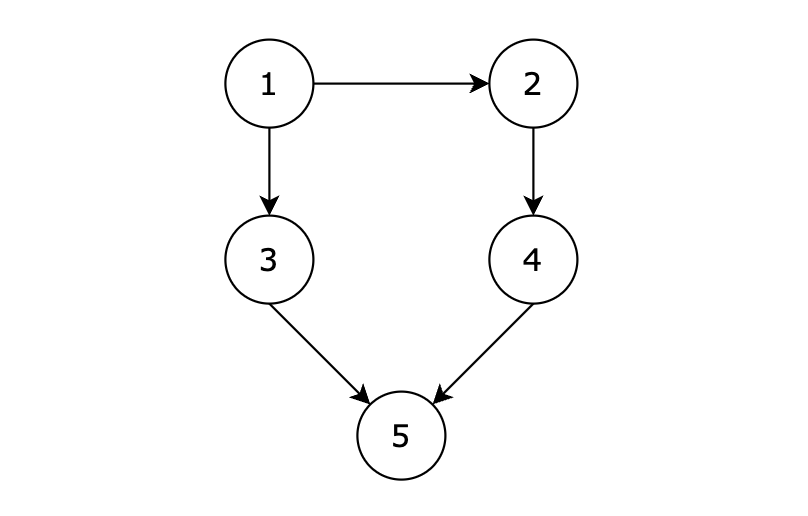
给定一个有 n 个节点的有向无环图,节点编号从 1 到 n。请编写一个函数,找出并返回所有从节点 1 到节点 n 的路径。每条路径应以节点编号的列表形式表示。
输入描述
第一行包含两个整数 N,M,表示图中拥有 N 个节点,M 条边
后续 M 行,每行包含两个整数 s 和 t,表示图中的 s 节点与 t 节点中有一条路径
输出描述
输出所有的可达路径,路径中所有节点之间空格隔开,每条路径独占一行,存在多条路径,路径输出的顺序可任意。如果不存在任何一条路径,则输出 -1。
注意输出的序列中,最后一个节点后面没有空格! 例如正确的答案是 `1 3 5`,而不是 `1 3 5 `, 5后面没有空格!
输入示例
5 5 1 3 3 5 1 2 2 4 4 5输出示例
1 3 5 1 2 4 5提示信息
用例解释:
有五个节点,其中的从 1 到达 5 的路径有两个,分别是 1 -> 3 -> 5 和 1 -> 2 -> 4 -> 5。
因为拥有多条路径,所以输出结果为:
1 3 5
1 2 4 5或
1 2 4 5
1 3 5
都算正确。数据范围:
- 图中不存在自环
- 图中不存在平行边
- 1 <= N <= 100
- 1 <= M <= 500
题解:dfs+邻接矩阵
求不同路径的问题,一般通过 dfs 来实现。
这题出的很经典,我们需要的就是不断搜索找到不同的路径使得从起始位置到达中终止位置。
需要注意的是:
1.这里用的节点 1 作为起始位置,那么初始化邻接矩阵,大小就应该为n+1;当然以节点 0 作为起始位置也可以,那么邻接矩阵大小就为 n ;
2.标记相连的方式:邻接矩阵中 graph[s][t] = 1 -- 用 1 表示 s 与 t 相连。
深度优先搜索函数 dfs:
1.参数包括邻接矩阵 graph、当前节点 x 和目标节点 n。
2.终止条件:如果当前节点 x 等于目标节点 n,则意味着找到了一条从起始节点到目标节点的路径。此时,将当前路径 path 添加到结果集 ans 中,并返回。
3.遍历相邻节点:对于当前节点 x,遍历所有可能的相邻节点(从1到n)。
4.如果节点 x 与节点 i 相连(即 graph[x][i] == 1),则执行以下步骤:
将节点 i 添加到当前路径 path 中;
递归调用 dfs 函数,从节点 i (与 x 相连接的节点)开始继续深度优先搜索;
在递归返回后,将节点 i 从路径 path 中移除,以实现回溯。
代码如下(其实就是 dfs 模板的应用):
#include<bits/stdc++.h>
using namespace std;
vector<vector<int>> ans; // 存放符合条件的路径 -- 存放结果
vector<int> path; // 起始位置(节点1)到终点的路径
void dfs (const vector<vector<int>>& graph, int x, int n) {
if (x == n) { // 终止条件:当前遍历的节点 x 到达节点 n,说明找到符合条件的一条路径
ans.push_back(path); //当前路径存入 ans
return;
}
for (int i = 1; i <= n; i++) { // 遍历节点 x 连接的所有节点
if (graph[x][i] == 1) { // 找到 x 连接的节点
path.push_back(i); // 遍历到的节点加入到路径中来
dfs(graph, i, n); // 进入下一层递归 -- 从当前 x 连接的 i 开始
path.pop_back(); // 回溯,撤销本节点
}
}
}
int main() {
int n, m, s, t;
cin >> n >> m;
vector<vector<int>> graph(n + 1, vector<int>(n + 1, 0)); // 初始化邻接矩阵,大小为n+1,因为节点编号从1开始
while (m--) {
cin >> s >> t;
graph[s][t] = 1; // 使用邻接矩阵表示无线图,1 表示 s 与 t 是相连的
}
path.push_back(1); // 将起始节点1加入到路径中 -- 后续dfs操作并不添加起始节点1
dfs(graph, 1, n); // 从节点1开始深度优先搜索
if (ans.size() == 0) { // 没有找到任何路径
cout<<"-1"<<endl;
}
for (const vector<int> &p : ans) { // 这里的 p 用来遍历 ans 的各个元素 -- 每个元素都是一条路径 path,需单独将这些路径打印
for (int i = 0; i < p.size() - 1; i++) { // 注意:当前路径最后一个元素后无空格 -- 遍历范围 0 -- size-2
cout << p[i] << " ";
}
cout << p[p.size() - 1] << endl; // 将每条路径最后一个元素单独提出来,从而防止最后结果多出一个空格
}
}三、小结
今天来到图论章节打卡的第一天,这一类问题并不简单,后边会继续进行相关内容的练习和打卡,希望终能有所收获。