代码随想录训练营 Day50打卡 图论part01
一、理论基础
DFS(深度优先搜索)和 BFS(广度优先搜索)在图搜索中的核心区别主要体现在搜索策略上:
1、搜索方向:
- DFS:深度优先,一条路走到黑。DFS
从起点开始,选择一个方向深入到底,遇到死胡同再回溯,换一个方向继续探索。这种方式适合解决路径和组合问题,常与递归和回溯算法结合使用。 - BFS:广度优先,层层推进。BFS 以起点为中心,一层层扩展,首先访问所有与起点相邻的节点,然后再访问这些节点的下一层。BFS通常用于找到最短路径或解决需要按层次遍历的问题。
2、使用的数据结构:
- DFS:采用 栈 结构实现(递归隐式使用栈,或者显式使用栈数据结构)。
- BFS:使用 队列 实现,遵循先入先出的原则,逐层访问节点。
3、空间和时间复杂度:
- DFS:占用的内存相对较少,因其只需要记录当前路径和回溯过程中的节点。时间复杂度是 O(V + E),其中 V 是节点数,E 是边的数量。空间复杂度与递归深度有关,最坏情况下可能达到 O(V)。
- BFS:需要存储每一层的节点,因此占用的内存较多。时间复杂度同样是 O(V + E),但空间复杂度通常是 O(V),因为要存储所有节点的状态和层次信息。
4、适用场景:
- DFS:适合解决需要遍历到图的某个具体位置、回溯路径、组合搜索等问题,例如解决迷宫问题、找路径的所有可能解。
- BFS:适合寻找最短路径或需要按层次访问图的场景,例如无权图中的最短路径问题。
DFS 框架简介
DFS 的基本框架依赖递归和回溯机制,关键在于路径处理和终止条件的设置:
void dfs(参数) {
if (终止条件) {
存放结果;
return;
}
for (选择:本节点所连接的其他节点) {
处理节点;
dfs(图,选择的节点); // 递归
回溯,撤销处理结果
}
}
DFS 通过递归深入到图的尽头,然后再逐步回溯,处理可能的路径和解。
BFS 框架简介
BFS 以层次展开,可以用队列实现,框架如下:
void bfs(参数) {
queue<Node> q;
q.push(起点);
while (!q.empty()) {
Node current = q.front();
q.pop();
for (每一个与 current 相邻的节点) {
处理节点;
q.push(相邻节点);
}
}
}
BFS 的每层处理完当前层所有节点后,再进入下一层,保证了广度搜索的特点。
总结:DFS 和 BFS 是两种经典的搜索策略,DFS 更侧重于深度探索和回溯,而 BFS 则侧重于广度的逐层推进。理解它们的区别和适用场景有助于在不同问题中灵活选择合适的算法。
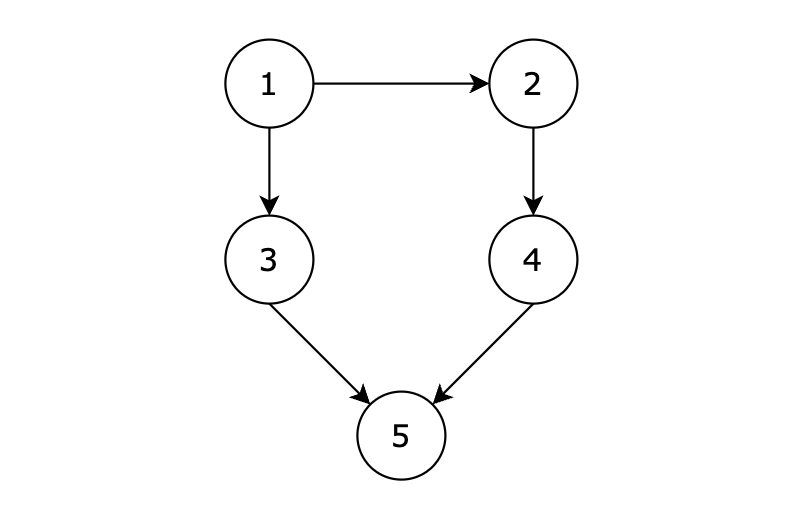
二、卡码98. 所有可达路径
题目描述
给定一个有 n 个节点的有向无环图,节点编号从 1 到 n。请编写一个函数,找出并返回所有从节点 1 到节点 n 的路径。每条路径应以节点编号的列表形式表示。
输入描述
第一行包含两个整数 N,M,表示图中拥有 N 个节点,M 条边
后续 M 行,每行包含两个整数 s 和 t,表示图中的 s 节点与 t 节点中有一条路径
输出描述
输出所有的可达路径,路径中所有节点之间空格隔开,每条路径独占一行,存在多条路径,路径输出的顺序可任意。如果不存在任何一条路径,则输出 -1。
注意输出的序列中,最后一个节点后面没有空格! 例如正确的答案是1 3 5,而不是1 3 5, 5后面没有空格!
输入示例
5 5
1 3
3 5
1 2
2 4
4 5
输出示例
1 3 5
1 2 4 5
提示信息
用例解释:
有五个节点,其中的从 1 到达 5 的路径有两个,分别是 1 -> 3 -> 5 和 1 -> 2 -> 4 -> 5。
因为拥有多条路径,所以输出结果为:
1 3 5
1 2 4 5
或
1 2 4 5
1 3 5
都算正确。
邻接矩阵写法
代码实现思路:
- 图的表示:使用二维数组(邻接矩阵)来存储图,graph[x][y] 表示从节点 x 到节点 y 是否有边,如果有边则值为 1,否则为
0。 - DFS 搜索:从节点 1 开始,使用深度优先搜索遍历图。如果到达终点(节点 n),将路径存储在 result
中。每次递归调用前将当前节点加入路径,递归结束时通过回溯移除该节点。 - 递归终止条件:当到达终点节点 n 时,将当前路径存储在结果中,递归停止。
- 结果处理:如果没有找到从节点 1 到终点的路径,输出 -1,否则输出所有路径。
def dfs(graph, x, n, path, result):
# 如果到达了终点(节点 n),将当前路径加入到结果中
if x == n:
result.append(path.copy()) # 复制当前路径,防止回溯时影响
return
# 遍历所有节点,看是否可以从当前节点 x 移动到节点 i
for i in range(1, n + 1):
if graph[x][i] == 1: # 如果 x 可以到达 i
path.append(i) # 将 i 节点加入路径
dfs(graph, i, n, path, result) # 继续深度优先搜索
path.pop() # 回溯,将最后加入的节点从路径中移除
def main():
# 输入节点数 n 和边数 m
n, m = map(int, input().split())
# 初始化邻接矩阵,大小为 (n+1) x (n+1),因为节点从 1 开始
graph = [[0] * (n + 1) for _ in range(n + 1)]
# 构建图,读入 m 条边
for _ in range(m):
s, t = map(int, input().split()) # 从 s 到 t 有一条边
graph[s][t] = 1 # 在邻接矩阵中记录这条边
result = [] # 存放所有从 1 到 n 的路径
dfs(graph, 1, n, [1], result) # 从节点 1 开始搜索,路径初始为 [1]
# 如果没有找到任何路径,输出 -1,否则输出所有路径
if not result:
print(-1)
else:
for path in result:
print(' '.join(map(str, path))) # 将路径输出为空格分隔的字符串
if __name__ == "__main__":
main()
邻接表写法
代码实现思路:
- 图的表示:使用 defaultdict(list)
存储图的邻接表,每个节点存储与之相邻的节点列表。与邻接矩阵不同,邻接表节省了空间,只存储实际存在的边。 - DFS 搜索:同样从节点 1 开始,使用深度优先搜索。当到达终点节点 n 时,将当前路径存储在 result
中。每次递归前将当前节点加入路径,递归结束时回溯。 - 结果处理:与邻接矩阵版本一样,输出结果或返回 -1。
from collections import defaultdict
result = [] # 收集所有从节点1到节点n的路径
path = [] # 当前路径
def dfs(graph, x, n):
# 如果当前节点是终点(节点 n),将路径存储到结果中
if x == n:
result.append(path.copy()) # 复制路径,防止回溯影响
return
# 遍历当前节点 x 的所有相邻节点
for i in graph[x]:
path.append(i) # 将当前节点加入路径
dfs(graph, i, n) # 递归搜索相邻节点
path.pop() # 回溯,撤销本节点
def main():
# 输入节点数 n 和边数 m
n, m = map(int, input().split())
# 初始化邻接表,使用 defaultdict 使得添加边更方便
graph = defaultdict(list)
# 构建图,输入 m 条边
for _ in range(m):
s, t = map(int, input().split()) # 从 s 到 t 有一条边
graph[s].append(t) # 在邻接表中添加这条边
path.append(1) # 从节点 1 开始,初始路径为 [1]
dfs(graph, 1, n) # 开始搜索
# 输出结果,如果没有路径输出 -1,否则输出路径
if not result:
print(-1)
else:
for pa in result:
print(' '.join(map(str, pa))) # 输出路径
if __name__ == "__main__":
main()
题目链接
题目文章讲解
总结:
- 邻接矩阵适合处理稠密图,表示简单但占用空间较大,尤其当图的节点较多但边较少时会浪费空间。
- 邻接表适合处理稀疏图,能够节省空间,适合处理边较少的场景。
- DFS在这两种表示方式中的思路是一致的,只是访问方式不同:邻接矩阵中遍历二维数组,邻接表中遍历相邻节点的列表。
- 两种方法都使用了 回溯 的思想,每次递归进入一个新的节点,遍历完后需要撤销操作,即 回溯到上一层,确保路径恢复到原始状态。