• 题目：PAConv: Position Adaptive Convolution with Dynamic Kernel Assembling on Point Clouds
• 来源：CVPR2021
• 机构：香港大学
• 论文：https://arxiv.org/abs/2103.14635
• 代码：https://github.com/CVMI-Lab/PAConv

前言

PAConv，全称为位置自适应卷积（Position Adaptive Convolution），是一种用于处理3D点云数据的通用卷积操作。不同于传统的2D卷积，PAConv通过根据点在三维空间中的位置动态组合卷积核。它的实现依赖于一个称为权重库（Weight Bank）的结构，该结构存储了基本的权重矩阵。这些矩阵通过一个称为ScoreNet的网络动态组合，ScoreNet根据点的位置关系学习如何自适应地组装这些卷积核。

PAConv的关键特点包括：

1. 动态卷积核组装：卷积核不是固定的，而是通过根据学习到的与位置相关的系数动态组合权重矩阵生成的。
2. 灵活性：相比于传统的2D卷积，PAConv更加灵活，特别适用于处理3D点云的不规则和无序特性。
3. 降低复杂度：PAConv通过组合预定义的矩阵来生成卷积核，而不是直接从点的位置预测卷积核，这降低了计算复杂度。
4. 与MLP网络集成：PAConv可以无缝集成到经典的点云处理框架（如PointNet或DGCNN）中，而无需改变其网络架构，同时还能显著提高在3D物体分类和分割任务中的表现。

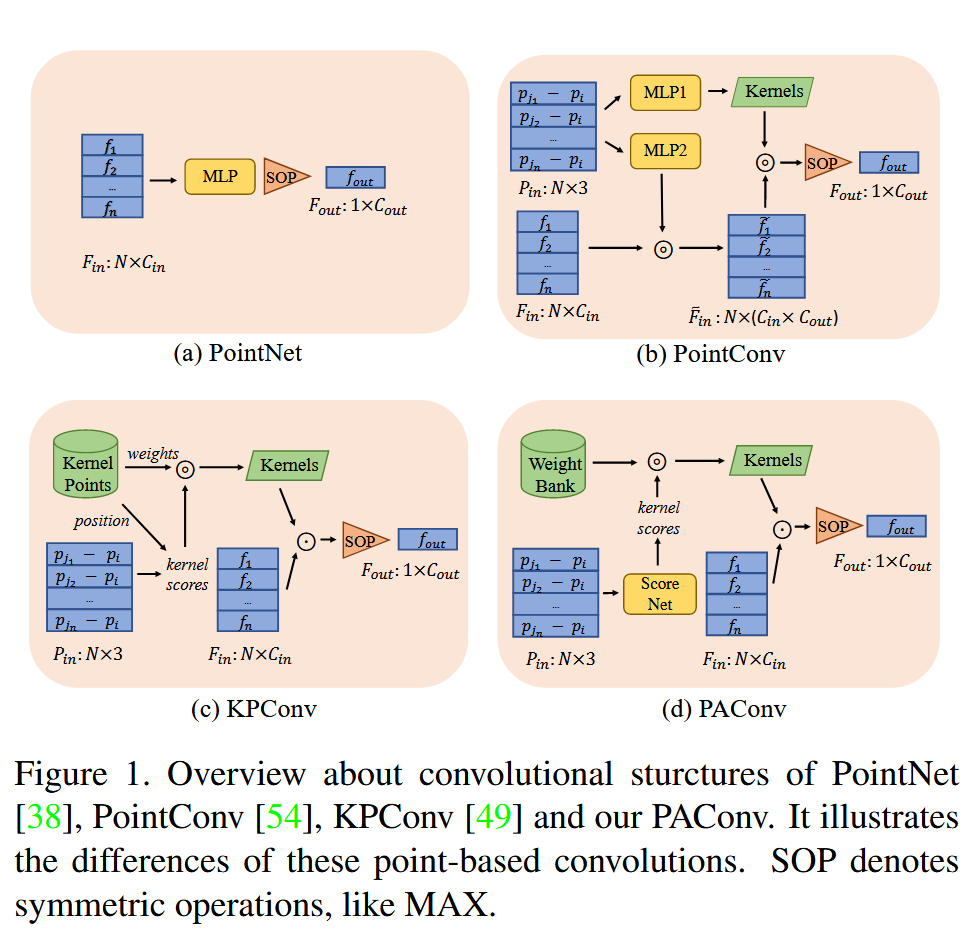
方法实现

PAConv（位置自适应卷积）的实现基于以下几个核心部分：动态卷积核组装、权重库（Weight Bank） 和 ScoreNet。其主要实现步骤如下：

PAConv 的实现通过 ScoreNet 根据点之间的位置信息动态组合权重库中的权重矩阵，生成适应点云不规则性的卷积核。这一过程不仅有效处理了 3D 点云的复杂空间结构，同时通过减少直接预测卷积核的计算负担，实现了较高的效率和性能提升。

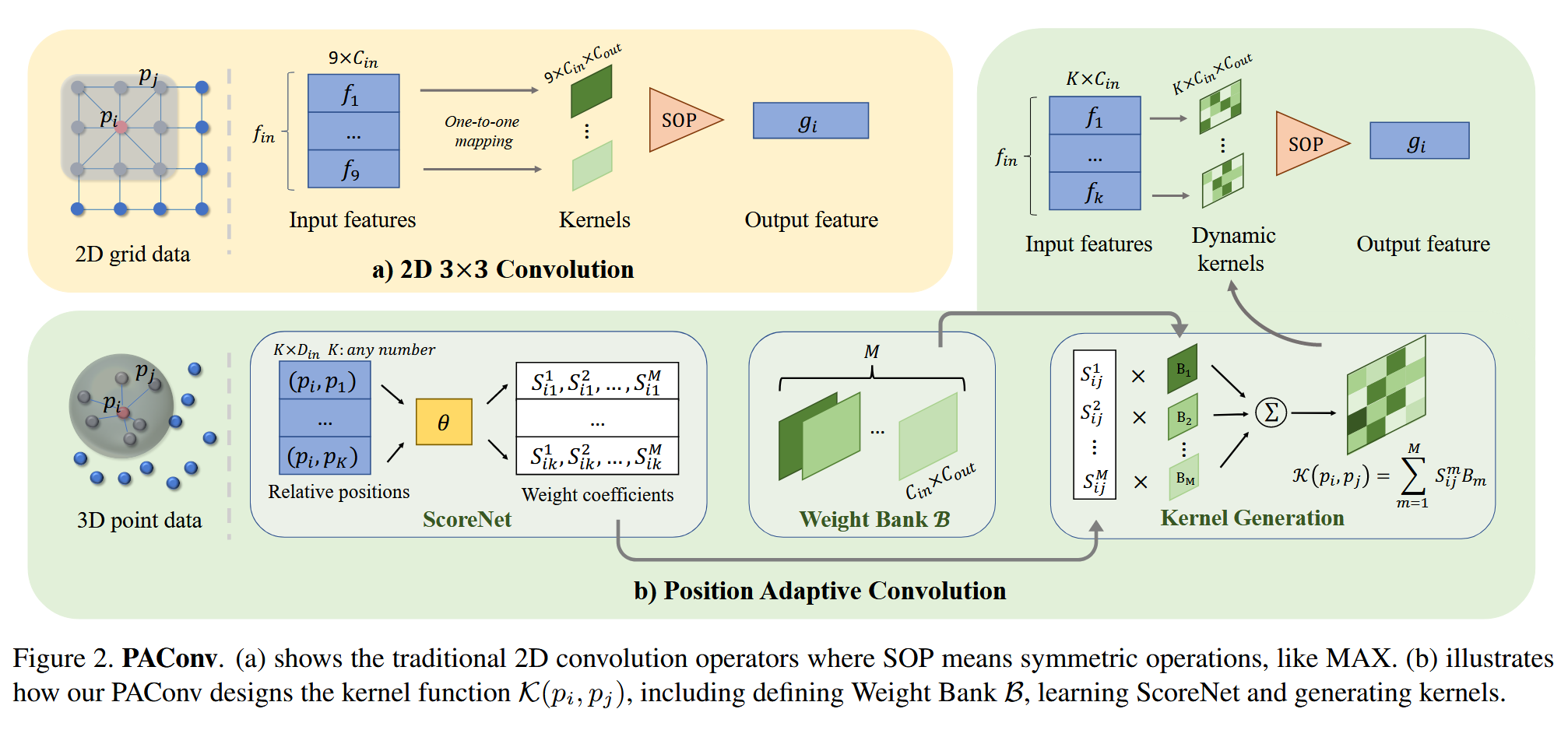
1. 权重库（Weight Bank）

PAConv 的第一个核心部分是权重库，它存储了多个基础的权重矩阵，记作 B = { B 1 , B 2 , … , B M } B = \{ B_1, B_2, \dots, B_M \} B={B1​,B2​,…,BM​}，其中每个矩阵 $B_m$ 的维度为 $C_{in}\times C_{out}$。这些矩阵不会直接用于卷积，而是通过后续的动态组合过程生成卷积核。

2. ScoreNet

ScoreNet 是一个多层感知器 (MLP)，用于学习点之间的位置信息，生成用于组合权重矩阵的系数。

ScoreNet 的输入是中心点 $p_i$ 和邻居点 $p_j$ 的位置信息 $(p_i,p_j)$，输出是一个归一化后的得分向量 $S_{ij}$，用于控制不同权重矩阵的组合。ScoreNet 的输出计算如下：
$S_{ij}=\alpha (\theta (p_i,p_j))$
其中：

• $\theta (p_i,p_j)$ 是通过 MLP 计算的非线性函数，提取点 $p_i$ 和 $p_j$ 之间的位置信息。
• $\alpha$ 是 Softmax 归一化函数，确保得分在 $(0,1)$ 之间。

输出的得分向量 S i j = { S i j 1 , S i j 2 , … , S i j M } S_{ij} = \{ S_{ij}^1, S_{ij}^2, \dots, S_{ij}^M \} Sij​={Sij1​,Sij2​,…,SijM​}，每个 $S_{ij}^m$ 对应权重矩阵 $B_m$ 的组合系数。

3. 动态卷积核的生成

使用 ScoreNet 输出的得分向量 $S_{ij}$，动态组合权重库中的权重矩阵，生成最终的卷积核 $K(p_i,p_j)$：
$K(p_i,p_j)={\sum }_{m=1}^M{S}_{ij}^m{B}^m$
其中：

• $K(p_i,p_j)$ 是点 $p_i$ 和 $p_j$ 之间的卷积核。
• $S_{ij}^m$ 是 ScoreNet 生成的组合系数，代表权重矩阵 $B_m$ 在生成卷积核时的权重。
• $B^m$ 是权重库中的第 $m$ 个权重矩阵。

4. 卷积操作

生成的卷积核 $K(p_i,p_j)$ 用于与输入特征 $F$ 进行卷积操作。对于给定点云的输入特征 F = { f 1 , f 2 , … , f N } F = \{ f_1, f_2, \dots, f_N \} F={f1​,f2​,…,fN​}，输出特征 G = { g 1 , g 2 , … , g N } G = \{ g_1, g_2, \dots, g_N \} G={g1​,g2​,…,gN​} 通过以下公式计算：
g i = Λ ( { K ( p i , p j ) f j ∣ p j ∈ N i } ) g_i = \Lambda\left(\left\{ K(p_i, p_j) f_j \mid p_j \in N_i \right\}\right) gi​=Λ({K(pi​,pj​)fj​∣pj​∈Ni​})
其中：

• $N_i$ 是中心点 $p_i$ 的邻居点集。
• $\Lambda$ 是用于聚合邻居点信息的操作（如 MAX、SUM 或 AVG）。
• $f_j$ 是邻居点 $p_j$ 的输入特征。
• $g_i$ 是点 $p_i$ 的输出特征。

5. 权重正则化

为了避免权重矩阵过于相似，PAConv 引入了权重正则化，确保权重库中的矩阵保持多样性。正则化的损失函数 $L_{corr}$ 通过减少权重矩阵之间的相关性来实现：
$L_{corr}={\sum }_{B_i,B_j\in B,i\ne j}\frac{|B_i\cdot B_j|}{||B_i|{|}_2||B_j|{|}_2}$
其中：

• $B_i$ 和 $B_j$ 是权重库中的两个不同权重矩阵。
• $||B_i|{|}_2$ 和 $||B_j|{|}_2$ 是权重矩阵的 $L_2$ 范数。
• $L_{corr}$ 用于最小化不同权重矩阵之间的相似性，确保生成的卷积核具有足够的多样性。

如何使用方法改进PointNet++网络

改进位置

• 动态卷积核替换 MLP 层：利用 PAConv 替代 MLP 层，使得 PointNet++ 更好地捕捉点云的空间关系和几何结构。