- 🍨 本文为🔗365天深度学习训练营 中的学习记录博客
- 🍖 原作者:K同学啊
目标:
- 逻辑回归适用于分类问题,主要用于解决二分类或多分类的问题。比如:用户购买某商品的可能性,某病人患有某种疾病的可能性等等;某个物品属于哪个类别等;
- 了解Sigmoid和Softmax的用法
具体实现:
(一)环境:
语言环境:Python 3.10
编 译 器: PyCharm
*框 架:*scikit-learn
**(二)具体步骤:
导入库:
import numpy as np
import pandas as pd
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import accuracy_score, classification_report, confusion_matrix
- 导入数据集:
# 导入数据集
iris = datasets.load_iris()
X = iris.data
Y = iris.target
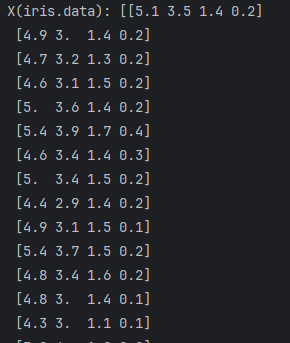
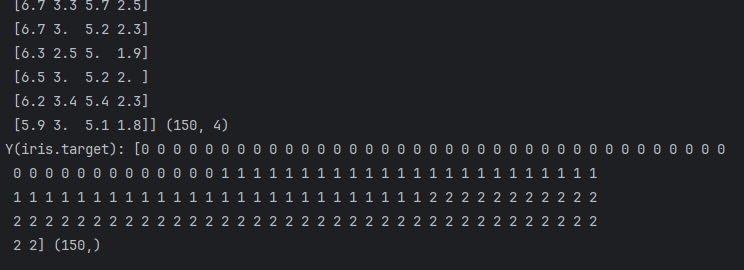
print("X(iris.data):", X, X.shape)
print("Y(iris.target):", Y, Y.shape)
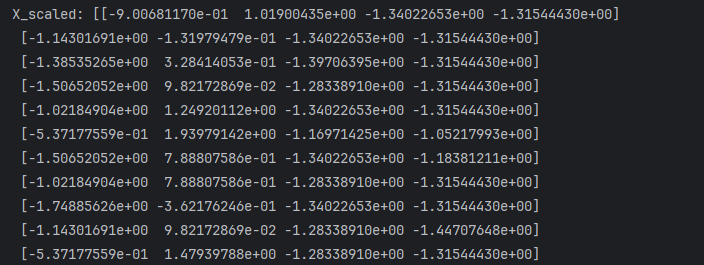
2. 数据预处理:特征标准化:
# 数据预处理:特征标准化
scaler = StandardScaler() # 将数据缩放到一个均值为 0,标准差为 1 的正态分布
X_scaled = scaler.fit_transform(X)
print("X_scaled:", X_scaled, X_scaled.shape)
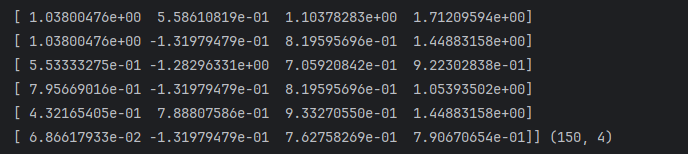
3. ** 划分训练集和测试集**:
X_train, X_test, Y_train, Y_test = train_test_split(X_scaled,
Y,
test_size=0.2,
random_state=42)
注:random_state参数设置成了42,会有什么效果?参考:train_test_split详解_train test split-CSDN博客
random_state:有三种结果,0或None:每次随机的数据集都不一样。整数(int):每次随机的数据集是一样的(固定的),一样的数据集就可以复现模型结果。如:把random_state设置成None,多执行几次代码,会发现准确率是不一样的。
4. 逻辑回归模型:
# 逻辑回归模型
from sklearn.linear_model import LogisticRegression
model = LogisticRegression(max_iter=200) # 默认迭代100次,这里设置成200次
model.fit(X_train, Y_train)
- 预测结果:
# 预测结果
y_pred = model.predict(X_test)
print("predictions:", y_pred)

6. 评估预测结果:
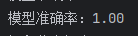
# 评估预测结果
accuracy = accuracy_score(Y_test, y_pred)
print("模型准确率:", accuracy)

# 精确一点,准确率保留两位小数点,格式化输出一下
print("模型准确率:%.2f" % accuracy)
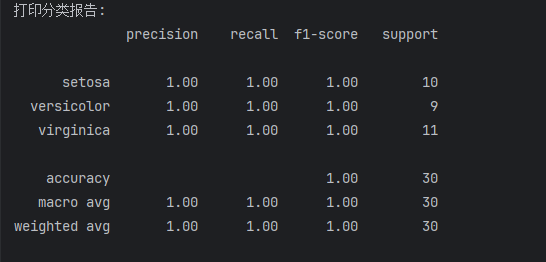
# 打印分类报告
print("打印分类报告:")
print(classification_report(Y_test, y_pred, target_names=iris.target_names))
注:
1.precision:准确率,表示模型在预测为正例的样本中,实际为正例的比例
2.recall:召回率,表示模型在实际为正例的样本中,成功预测为正例的比例
3.f1-score:F1分数,综合精确度和召回率的指标,是精确度和召回率的调和均值
4.support:支持度,表示每个类别在实际数据中的样本数量
# 打印混淆矩阵
print("混淆矩阵:")
print(confusion_matrix(Y_test, y_pred))
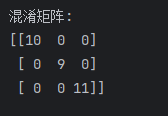
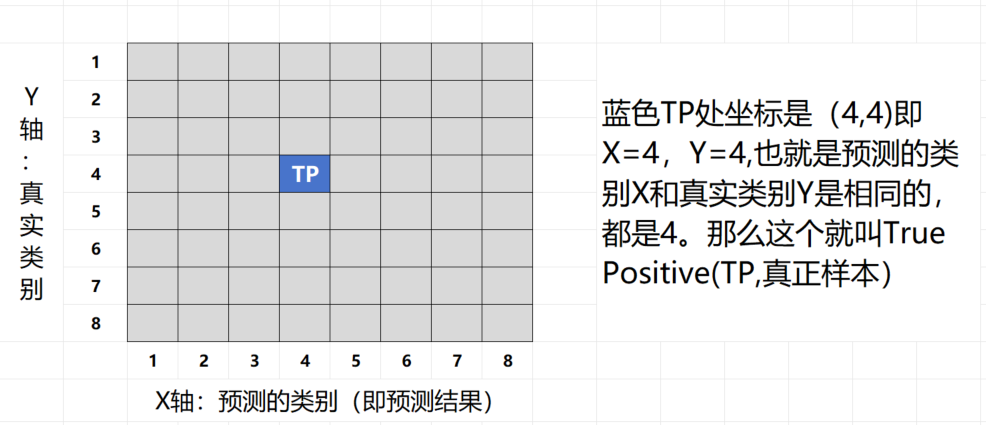
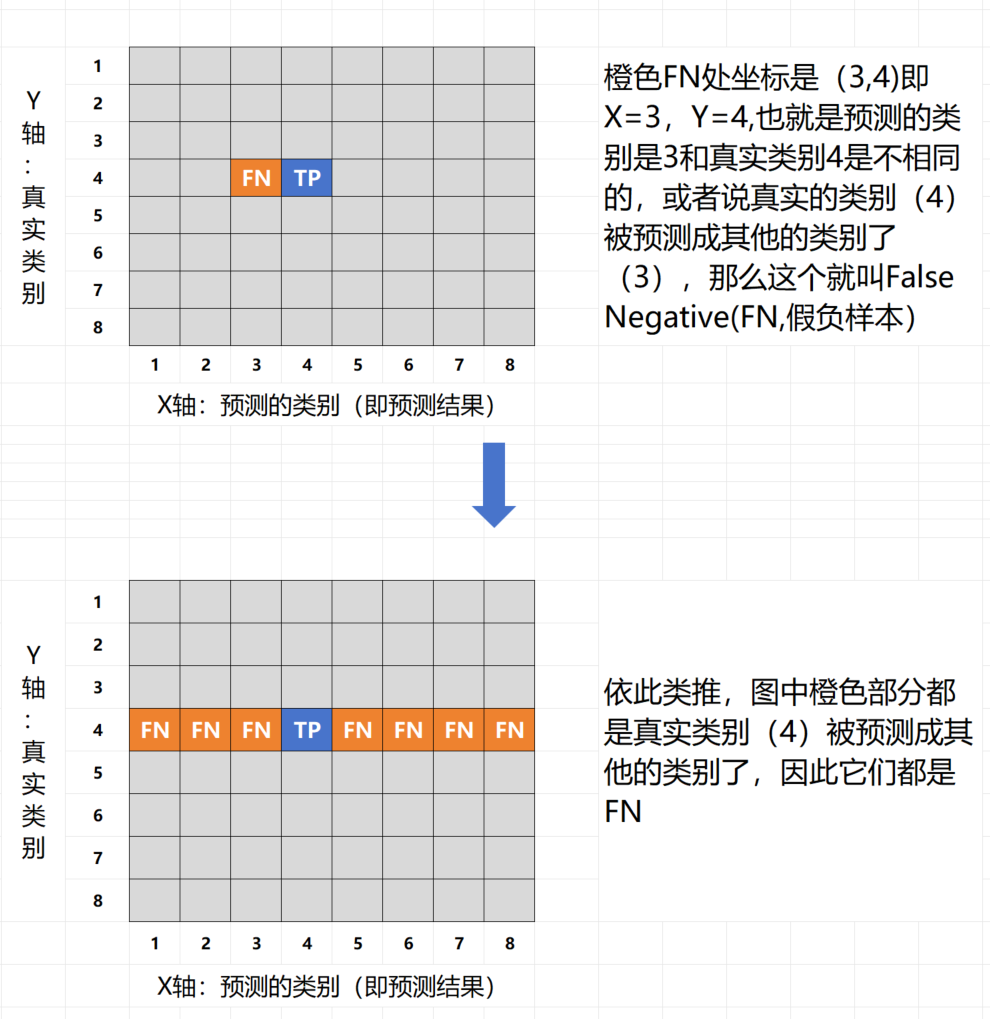
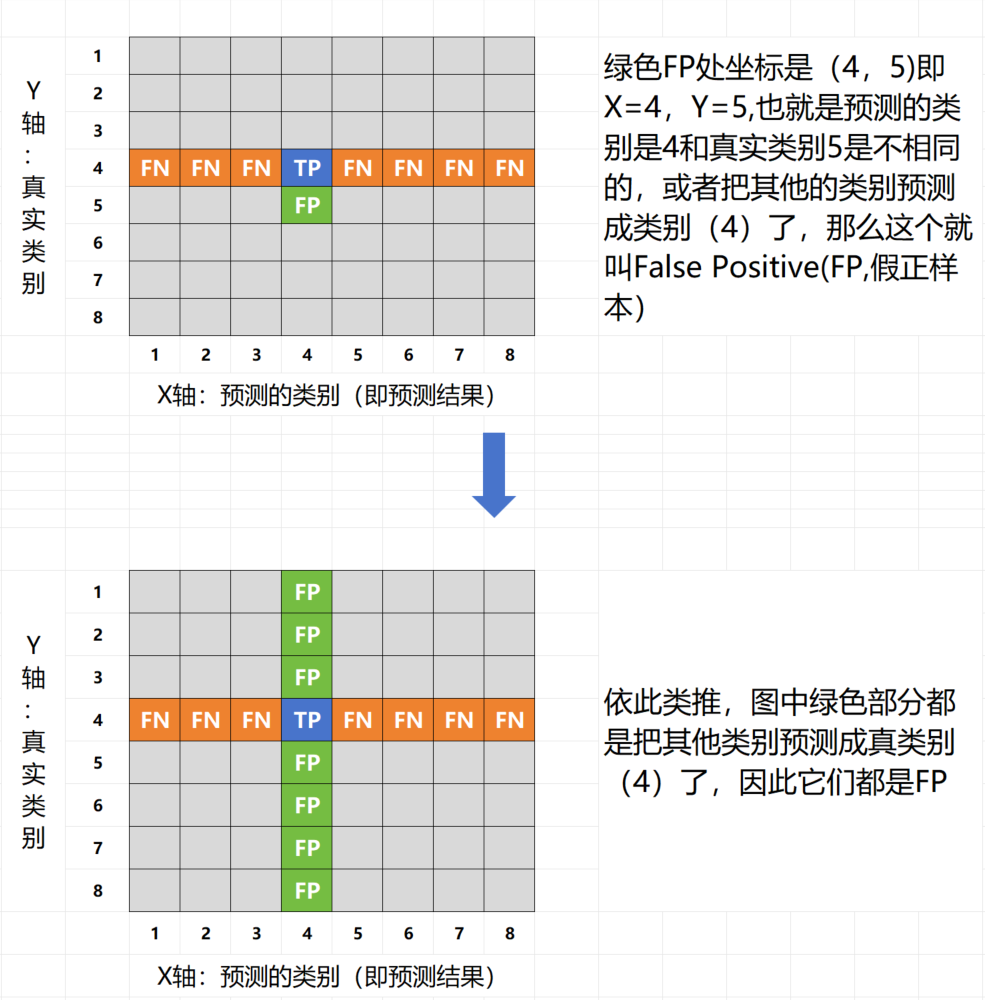
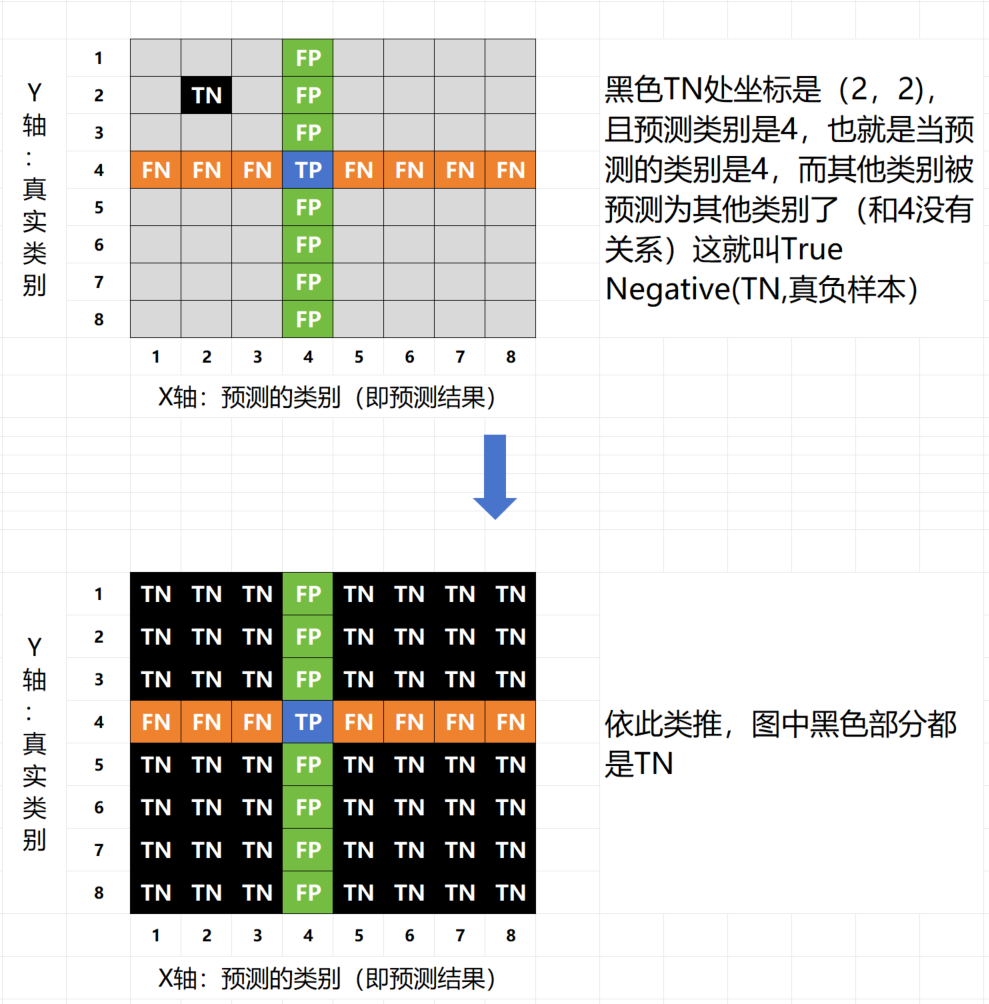
在机器学习和数据科学领域,混淆矩阵(Confusion Matrix)是一种常用的性能度量工具,尤其在分类问题中。它提供了分类模型性能的可视化表示,帮助我们深入理解模型的分类效果。混淆矩阵以矩阵的形式展示了真实类别与模型预测类别之间的关系。混淆矩阵的每一行代表实际类别,每一列代表预测类别。通过混淆矩阵,我们可以清晰地看到每个类别的真正例(True Positive, TP)、假正例(False Positive, FP)、真反例(True Negative, TN)和假反例(False Negative, FN)的数量。参考:zhuanlan.zhihu.com/p/471327487,假设预测的结果(类别)是4,做个示意图分解一下: