985 闭眼
今天在牛客上看到一篇直呼好家伙的帖子:
这位同学指出:论坛里个个 985 的硕士闭着眼睛都有 15k 以上的月薪,还天天嚷嚷着研究生白读了,天天嚷嚷着反向读研了 ...
通常这样的帖子,都会被评论区喷成筛子。
结果打开评论区一看,大家都正儿八经在吐苦水,由此可见,过去几年选读研的同学,有不在少数是真觉得后悔:

一个最现实的情况:如果三年前 985 或 211 的本科,和如今的硕士找的工作是一样的,价格也没区别,那就是"反向读研"。
确实,如果读研没有带来就业优势,年龄反而增大了三岁,这对于国内互联网来说是明显的劣势。
如果再考虑时代的因素,那可能对人生轨迹的影响就更大了。
读研与否所导致的经济差,远远不止读研费用(负收入)和就业薪资(正收入)之间的差别,还在于就业机会和先发优势。
我举个例子你就明白了,三年前要加入大厂是相对容易的,现在找个工作都难;即使能力足够强,读完研还能进入大厂,且拿到比本科就业时更高的 base,但当年的本科早进来三年的同届舍友可能已经是个小 leader,在晋升和职业规划上,早就领先几个身位;如果恰好这三年公司处于高速上升期的话,那很可能这三年到手的奖金和期权,就已经能抵这个硕士同事的十年收入了 ...
对此,你怎么看?
你读研了吗?你觉得如今的就业市场和四年前相比,有何区别?
...
回归主题。
来一道循序渐进算法题。
题目描述
平台:LeetCode
题号:978
当 A 的子数组
满足下列条件时,我们称其为湍流子数组:
-
若 ,当 为奇数时, ,且当 为偶数时, -
若 ,当 为偶数时, ,且当 为奇数时,
也就是说,如果比较符号在子数组中的每个相邻元素对之间翻转,则该子数组是湍流子数组。
返回 A 的最大湍流子数组的长度。
示例 1:
输入:[9,4,2,10,7,8,8,1,9]
输出:5
解释:(A[1] > A[2] < A[3] > A[4] < A[5])
示例 2:
输入:[4,8,12,16]
输出:2
示例 3:
输入:[100]
输出:1
提示:
基本思路
本题其实是要我们求最长一段呈 ↗ ↘ ↗ ↘ 或者 ↘ ↗ ↘ ↗ 形状的数组长度。
看一眼数据范围,有 40000,那么枚举起点和终点,然后对划分出来的子数组检查是否为「湍流子数组」的朴素解法就不能过了。
朴素解法的复杂度为 ,直接放弃朴素解法。
复杂度往下优化,其实就 的 DP 解法了。
动态规划
至于 DP 如何分析,通过我们会先考虑一维 DP 能否求解,不行再考虑二维 DP。
对于本题,「由于每个位置而言,能否「接着」上一个位置」形成「湍流」,取决于上一位置是由什么形状而来。
举个例子,对于样例 [3,4,2],从 4 -> 2 已经确定是 ↘ 状态,那么对于 2 这个位置能否「接着」4 形成「湍流」,要求 4 必须是由 ↗ 而来。
「因此我们还需要记录某一位是如何来的(↗ 还是 ↘),需要使二维 DP 来求解」
我们定义
代表以位置 i 为结尾,而结尾状态为 j 的最长湍流子数组长度(0:上升状态 / 1:下降状态)
❝PS. 这里的状态定义我是猜的,这其实是个技巧。通常我们做 DP 题,都是先猜一个定义,然后看看这个定义是否能分析出状态转移方程帮助我们「不重不漏」的枚举所有的方案。一般我是直接根据答案来猜定义,这里是求最长子数组长度,所以我猜一个 f(i,j) 代表最长湍流子数组长度
❞
不失一般性考虑
该如何求解,我们知道位置 i 是如何来是唯一确定的(取决于
和
的大小关系),而只有三种可能性:
-
:该点是由上升而来,能够「接着」的条件是 是由下降而来。则有: -
:改点是由下降而来,能够「接着」的条件是 是由上升而来。则有: -
:不考虑,不符合「湍流」的定义
Java 代码:
class Solution {
public int maxTurbulenceSize(int[] arr) {
int n = arr.length, ans = 1;
int[][] f = new int[n][2];
f[0][0] = f[0][1] = 1;
for (int i = 1; i < n; i++) {
f[i][0] = f[i][1] = 1;
if (arr[i] > arr[i - 1]) f[i][0] = f[i - 1][1] + 1;
else if (arr[i] < arr[i - 1]) f[i][1] = f[i - 1][0] + 1;
ans = Math.max(ans, Math.max(f[i][0], f[i][1]));
}
return ans;
}
}
C++ 代码:
class Solution {
public:
int maxTurbulenceSize(vector<int>& arr) {
int n = arr.size(), ans = 1;
vector<vector<int>> f(n, vector<int>(2, 1));
for (int i = 1; i < n; i++) {
if (arr[i] > arr[i - 1]) f[i][0] = f[i - 1][1] + 1;
else if (arr[i] < arr[i - 1]) f[i][1] = f[i - 1][0] + 1;
ans = max(ans, max(f[i][0], f[i][1]));
}
return ans;
}
};
Python 代码:
class Solution:
def maxTurbulenceSize(self, arr: List[int]) -> int:
n, ans = len(arr), 1
f = [[1, 1] for _ in range(n)]
for i in range(1, n):
if arr[i] > arr[i - 1]:
f[i][0] = f[i - 1][1] + 1
elif arr[i] < arr[i - 1]:
f[i][1] = f[i - 1][0] + 1
ans = max(ans, max(f[i][0], f[i][1]))
return ans
TypeScript 代码:
function maxTurbulenceSize(arr: number[]): number {
let n = arr.length, ans = 1;
const f: number[][] = new Array(n).fill(0).map(() => [1, 1]);
for (let i = 1; i < n; i++) {
if (arr[i] > arr[i - 1]) f[i][0] = f[i - 1][1] + 1;
else if (arr[i] < arr[i - 1]) f[i][1] = f[i - 1][0] + 1;
ans = Math.max(ans, Math.max(f[i][0], f[i][1]));
}
return ans;
};
-
时间复杂度: -
空间复杂度:
空间优化:奇偶滚动
我们发现对于 状态的更新只依赖于 的状态。
因此我们可以使用「奇偶滚动」方式来将第一维从 n 优化到 2。
修改的方式也十分机械,只需要改为「奇偶滚动」的维度直接修改成 2,然后该维度的所有访问方式增加 %2 或者 &1 即可:
Java 代码:
class Solution {
public int maxTurbulenceSize(int[] arr) {
int n = arr.length, ans = 1;
int[][] f = new int[2][2];
f[0][0] = f[0][1] = 1;
for (int i = 1; i < n; i++) {
f[i % 2][0] = f[i % 2][1] = 1;
if (arr[i] > arr[i - 1]) f[i % 2][0] = f[(i - 1) % 2][1] + 1;
else if (arr[i] < arr[i - 1]) f[i % 2][1] = f[(i - 1) % 2][0] + 1;
ans = Math.max(ans, Math.max(f[i % 2][0], f[i % 2][1]));
}
return ans;
}
}
C++ 代码:
class Solution {
public:
int maxTurbulenceSize(vector<int>& arr) {
int n = arr.size(), ans = 1;
vector<vector<int>> f(2, vector<int>(2, 1));
for (int i = 1; i < n; i++) {
f[i % 2][0] = f[i % 2][1] = 1;
if (arr[i] > arr[i - 1]) f[i % 2][0] = f[(i - 1) % 2][1] + 1;
else if (arr[i] < arr[i - 1]) f[i % 2][1] = f[(i - 1) % 2][0] + 1;
ans = max(ans, max(f[i % 2][0], f[i % 2][1]));
}
return ans;
}
};
Python 代码:
class Solution:
def maxTurbulenceSize(self, arr: List[int]) -> int:
n, ans = len(arr), 1
f = [[1, 1] for _ in range(2)]
for i in range(1, n):
f[i % 2][0] = f[i % 2][1] = 1
if arr[i] > arr[i - 1]:
f[i % 2][0] = f[(i - 1) % 2][1] + 1
elif arr[i] < arr[i - 1]:
f[i % 2][1] = f[(i - 1) % 2][0] + 1
ans = max(ans, max(f[i % 2][0], f[i % 2][1]))
return ans
TypeScript 代码:
function maxTurbulenceSize(arr: number[]): number {
let n = arr.length, ans = 1;
const f: number[][] = [[1, 1], [1, 1]];
for (let i = 1; i < n; i++) {
f[i % 2][0] = f[i % 2][1] = 1;
if (arr[i] > arr[i - 1]) f[i % 2][0] = f[(i - 1) % 2][1] + 1;
else if (arr[i] < arr[i - 1]) f[i % 2][1] = f[(i - 1) % 2][0] + 1;
ans = Math.max(ans, Math.max(f[i % 2][0], f[i % 2][1]));
}
return ans;
};
-
时间复杂度: -
空间复杂度:使用固定 2 * 2的数组空间。复杂度为
空间优化:维度消除
既然只需要记录上一行状态,能否直接将行的维度消除呢?
答案是可以的,当我们要转移第 i 行的时候,
装的就已经是 i-1 行的结果。
这也是著名「背包问题」的一维通用优手段。
但相比于「奇偶滚动」的空间优化,这种优化手段只是常数级别的优化(空间复杂度与「奇偶滚动」相同),而且优化通常涉及代码改动。
Java 代码:
class Solution {
public int maxTurbulenceSize(int[] arr) {
int n = arr.length, ans = 1;
int[] f = new int[2];
f[0] = f[1] = 1;
for (int i = 1; i < n; i++) {
int a = f[0], b = f[1];
f[0] = arr[i - 1] < arr[i] ? b + 1 : 1;
f[1] = arr[i - 1] > arr[i] ? a + 1 : 1;
ans = Math.max(ans, Math.max(f[0], f[1]));
}
return ans;
}
}
C++ 代码:
class Solution {
public:
int maxTurbulenceSize(vector<int>& arr) {
int n = arr.size(), ans = 1;
vector<int> f(2, 1);
for (int i = 1; i < n; ++i) {
int a = f[0], b = f[1];
f[0] = arr[i - 1] < arr[i] ? b + 1 : 1;
f[1] = arr[i - 1] > arr[i] ? a + 1 : 1;
ans = max(ans, max(f[0], f[1]));
}
return ans;
}
};
Python 代码:
class Solution:
def maxTurbulenceSize(self, arr: List[int]) -> int:
n, ans = len(arr), 1
f = [1, 1]
for i in range(1, n):
a, b = f[0], f[1]
f[0] = b + 1 if arr[i - 1] < arr[i] else 1
f[1] = a + 1 if arr[i - 1] > arr[i] else 1
ans = max(ans, max(f[0], f[1]))
return ans
TypeScript 代码:
function maxTurbulenceSize(arr: number[]): number {
let n = arr.length, ans = 1;
let f = [1, 1];
for (let i = 1; i < n; i++) {
let [a, b] = f;
f[0] = arr[i - 1] < arr[i] ? b + 1 : 1;
f[1] = arr[i - 1] > arr[i] ? a + 1 : 1;
ans = Math.max(ans, Math.max(f[0], f[1]));
}
return ans;
};
-
时间复杂度: -
空间复杂度:
最后
巨划算的 LeetCode 会员优惠通道目前仍可用 ~
使用福利优惠通道 leetcode.cn/premium/?promoChannel=acoier,年度会员 有效期额外增加两个月,季度会员 有效期额外增加两周,更有超大额专属 🧧 和实物 🎁 福利每月发放。
我是宫水三叶,每天都会分享算法知识,并和大家聊聊近期的所见所闻。
欢迎关注,明天见。
更多更全更热门的「笔试/面试」相关资料可访问排版精美的 合集新基地 🎉🎉


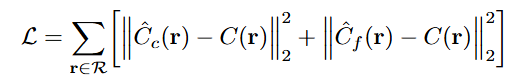












![[Linux] 权限](https://i-blog.csdnimg.cn/direct/edbba5bbe0bd4fc59885614068aa03af.png)


