统计学第5天

news2024/9/21 0:33:36

要观察性别和在线上买不买生鲜食品有没有关系，在现实生活中，女性通常去菜市场买菜的比较多，那么在线下是不是也是这样呢？

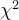$\chi^2$ 卡方统计量

如果研究的是两个类别变量，每个变量有多个类别，通常将两个变量多个类别的频数用交叉表的形式表示出来。其中一个变量放在行（row）的位置，称为行变量，其类别数（行数）用R表示，另一个变量放在列（column）的位置，称为列变量，其类别数（列数）用C表示。

这种由两个或着两个以上类别变量交叉分类的频数分布表称为列联表。一个由R行和C列组成的列联表称为R*C列联表。

对列联表中的两个类别变量进行分析，通常判断两个变量是否独立。该检验的假设是：

两个变量独立（无关），如果原假设被拒绝，则表明两个变量不独立，或者说两个变量不相关。

定义

1、用于检验列联表中变量之间拟合优度和独立性

2、检验统计量为： $x^2= \sum \frac{(f_o-f_e)^2}{f_e} \sim x^2(C-1)$ 【fo实际频数，fe期望频数】

或者 $x^2= \sum_{i=1}^{r}\sum_{j=1}^{c}\frac{(f_{ij}-e_{ij})^2}{e_{ij}} \sim x^2((R-1)(C-1))$ , $f_{ij}$ 表示列联表中第i行第j列类别中的实际频数， $e_{ij}$ 表示列联表中第i行第j列类别中的期望频数。

3、 $x^2$ 统计量可以看作是检验统计量与真实值与期望值的近似程度。两者越接近，即 $f_o-f_e$ 的绝对值越小，计算出的 $x^2$ 值就越小；反之， $f_o-f_e$ 的绝对值越大，计算出的 $x^2$ 值就越大。

性质

1、 $x^2\geq 0$ ，因为它是对平方结果的汇总；

2、分布与自由度的关系

由上图可以看出，自由度越小，分布就越往左边倾斜，随着自由度的增加， $x^2$ 分布的偏斜程度趋于缓解，逐渐显露出对称性。随着自由度的继续增大， $x^2$ 分布将趋近于对称的正态分布。

拟合优度检验

1、 $x^2$ 检验是利用 $x^2$ 分布对与分类数据的频数进行分析的统计学方法；

2、通过对 $x^2$ 的计算结果与 $x^2$ 分布中的临界值进行比较，做出是否拒绝原假设的统计决策；

3、 $x^2$ 检验的应用主要表现在两个方面：拟合优度检验和独立性检验。

（1）拟合优度检验是用 $x^2$ 统计量进行统计显著性检验的重要内容；

（2）检验的步骤

a依据总体分布状况，计算出分类变量各类别的期望频数；

b与分布的观察频数进行对比；

c判断期望频数与观察频数是否有显著差异，得出结论。

例1：1912年4月15，豪华巨轮泰坦尼克号与冰川相撞沉没。当时船上共有2208人，其中男性1738人，女性470人，海难发生后，幸存者共718人，其中男性374人，女性344人，以 $\alpha =0.05$ 的显著性水平检验存活情况与性别是否有关。

解答：在本例中需要判断观察频数与期望频数是否一致。

$H_0$ ：观察频数与期望频数一致；

$H_1$ ：观察频数与期望频数不一致。

计算过程如下表：（718/2208*1738）

自由度的计算公式为 $df=R-1$ ,R为分类变量类型的个数。

在本例中，分类变量是性别，有男、女两个类别，故R=2，自由度df=2-1=1。

经查 $\chi^2$ 分布表， $\chi^2_{0.05}(1)= 3.841$ ,括号中的数字表示自由度。

因为 $\chi^2$ 远大于 $\chi^2_{0.1}$ ，故拒绝H0，接收H1，说明存活状况与性别显著相关

独立性检验

拟合优度检验是对一个分类变量的检验，有时我们会遇到两个分类变量的问题，看这两个分类变量之间是否存在联系。例如原料有不同的等级，原料又产自不同的地区。原料等级和原料生产地就是两个分类变量。我们关心这两者是否有关联，是不是某些地区生产的原料有更好的质量。对这两个分类变量的分析，称为独立性检验。

例2：一份原料来自三个不同的地区，原料质量被分为三个不同的等级。从这批原料中随机抽取500件进行检验，结果如表表示，要求检验各个地区和原料等级之间是否存在依赖关系 $(\alpha=0.05)$

解答：

H0：地区和原料等级之间是独立的（不存在依赖关系）

H1：地区和原料等级之间不独立（存在依赖关系）

分析的关键是获取期望值

在第一行，甲地区的合计为140，用140/500作为甲地区原料比例的估计值。在第一列，一级原料的合计为162，用160/500作为一级原料比例的估计值。如果地区和原料等级之间是独立的，则可以用下面的公式估计第一个单元（甲地区，一级）中的期望比例。

令： A=样本单位来自甲地区的事件

B=样本单位属于一级原料的事件

根据独立性的概率乘法公式，有

P（第一个单元）=P（A）P（B）=（140/500）（162/500）=0.09072
0.09072是第一个单元中的期望比例，相应的频数期望为：0.09072 X 500 = 45.36

一般地，可以采用下式计算任意一个单元中频数的期望值：

$f_e=\frac{RT}{n}\times \frac{CT}{n} \times n = \frac{RT\times CT}{n}$

式中，fe为给定单元格的频数期望值；RT为给定单元格所在行的合计；CT为给定单元格所在列的合计；n为观察值的总个数（样本量）。

根据上式可以得到如下表所示的计算结果。

$x^2$ 的自由度为（R-1）（C-1）= 4

令 $\alpha = 0.05$ ，查表可知 $x^2_{0.05}(4)=9.488$

由于， $x^2>x^2_{0.05}(4)$ 故拒绝H0，接收H1，即地区和原料等级之间存在依赖关系，原料的质量受地区的影响。

例3：荔枝数码公司针对即将推出的手机制定一项推广方案，从所属的四个平台旗舰店中共随机抽取420名职工，了解他们对推广方案的态度（见下表），以 $\alpha=0.1$ 的显著性水平检验员工态度是否受所在平台的影响。

解答：若员工对推广方案的态度不受所在子公司的影响，四个平台对赞成推广方案的比例是一致的。设 $\pi_i$ 为第i个分公司赞成推广方案的百分比，可设定原假设和备择假设分别为：

$H_0:\pi_1=\pi_2=\pi_3=\pi_4$

$H_1:\pi_1,\pi_2,\pi_3,\pi_4$ 不全相等

统计量 $x^2 = \sum_{j=1}^{c}\frac{(f_o-f_e)^2}{f_e}=1.10163$

$x^2$ 的自由度=（R-1）（C-1）=3

令 $\alpha=0.1$ ,查表知道=： $x^2_{0.1}(3)=6.25$

由于 $x^2>x^2_{0.1}(3)$ ,故做出决策：在α=0.1的水平上不能拒绝H0.

结论：分公司不同与改革方案赞成比例之间不存在依赖关系，即可以认为四个分公司岁改革方案的赞成比例是一致的。

$x^2$ x方分布表

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/2098406.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！