bitset/bitmap
给40亿个不重复的无符号整数,没排过序。给1个无符号整数,如何快速判断一个数是否在这40亿个数中。

#pragma once
#include <vector>
#include <string>
#include <time.h>
template<size_t N>
class bitset
{
public:
bitset()
{
_bits.resize(N/8 + 1, 0);
}
void set(size_t x)
{
size_t i = x / 8;
size_t j = x % 8;
_bits[i] |= (1 << j);//将对应的比特位设置成为1
}
void reset(size_t x)
{
size_t i = x / 8;//计算x映射的位在第i个char数组位置
size_t j = x % 8;//计算x映射的位在这个char的第j个比特位
_bits[i] &= ~(1 << j);//和0与是0,和1与不变。
}
bool test(size_t x)//查看x在不在
{
size_t i = x / 8;
size_t j = x % 8;
return _bits[i] & (1 << j);
}
private:
vector<char> _bits;
};
void test_bitset1()
{
bitset<100> bs;
bs.set(10);
bs.set(11);
bs.set(15);
cout << bs.test(10) << endl;
cout << bs.test(15) << endl;
bs.reset(10);
cout << bs.test(10) << endl;
cout << bs.test(15) << endl;
bs.reset(10);
bs.reset(15);
cout << bs.test(10) << endl;
cout << bs.test(15) << endl;
}
void test_bitset2()
{
//bitset<-1> bs1;//传-1可以开最大的空间42亿多
bitset<0xFFFFFFFF> bs1;//这样写也可以开最大的空间42亿多
}
twobitset
给定100亿个整数,设计算法找到只出现1次的整数?
//用两个bitset封装
template<size_t N>
class twobitset
{
public:
void set(size_t x)
{
// 00 -> 01
if (_bs1.test(x) == false
&& _bs2.test(x) == false)
{
_bs2.set(x);
}
else if (_bs1.test(x) == false
&& _bs2.test(x) == true)
{
// 01 -> 10
_bs1.set(x);
_bs2.reset(x);
}
// 10代表至少出现两次,就不变化了。
}
void Print()//打印只出现一次的整数
{
for (size_t i = 0; i < N; ++i)
{
if (_bs2.test(i))
{
cout << i << endl;
}
}
}
public:
bitset<N> _bs1;
bitset<N> _bs2;
};
void test_twobitset()
{
int a[] = { 3, 45, 53, 32, 32, 43, 3, 2, 5, 2, 32, 55, 5, 53,43,9,8,7,8 };
twobitset<100> bs;
for (auto e : a)
{
bs.set(e);
}
bs.Print();
}
1.给两个文件,分别有100亿个整数,我们只有1G内存,如何找到两个文件交集?
方法1:其中一个文件的值,读到内存的一个位图中再读取另一个文件,判断在不在上面位图中,在就是交集!存在问题:找出来的交集存在重复的值。
方法2:
遍历,if(bs1.test(i)&&bs2.test(i))就是交集。
2.1个文件有100亿个int,1G内存,设计算法找到出现次数不超过2次的所有整数。和twobitset问题类似,00(出现0次)->01(出现1次)->10(出现2次)->11(出现3次)
位图的优点就是速度快、节省空间;缺点是只能映射整形,其他类型如:浮点数、string等等不能存储映射。
布隆过滤器
布隆过滤器减少磁盘IO或者网络请求,因为一旦一个值必定不存在的话,我们可以不用进行后续昂贵的查询请求。布隆过滤器正常情况下是不支持reset的。
struct BKDRHash//仿函数,将一个字符串转成整型。
{
size_t operator()(const string& s)
{
size_t hash = 0;
for (auto ch : s)
{
hash += ch;
hash *= 31;
}
return hash;
}
};
struct APHash
{
size_t operator()(const string& s)
{
size_t hash = 0;
for (long i = 0; i < s.size(); i++)
{
size_t ch = s[i];
if ((i & 1) == 0)
{
hash ^= ((hash << 7) ^ ch ^ (hash >> 3));
}
else
{
hash ^= (~((hash << 11) ^ ch ^ (hash >> 5)));
}
}
return hash;
}
};
struct DJBHash
{
size_t operator()(const string& s)
{
size_t hash = 5381;
for (auto ch : s)
{
hash += (hash << 5) + ch;
}
return hash;
}
};
// N最多会插入key数据的个数
template<size_t N,
class K = string,
class Hash1 = BKDRHash,
class Hash2 = APHash,
class Hash3 = DJBHash>//Hash是将K转换成为整型,这里是一个key映射到三个位置。
class BloomFilter
{
public:
void set(const K& key)
{
size_t len = N*_X;
size_t hash1 = Hash1()(key) % len;
_bs.set(hash1);
size_t hash2 = Hash2()(key) % len;
_bs.set(hash2);
size_t hash3 = Hash3()(key) % len;
_bs.set(hash3);
//cout << hash1 << " " << hash2 << " " << hash3 << " " << endl << endl;
}
bool test(const K& key)//需要三个位置在才能证明这个key值存在
{
size_t len = N*_X;
size_t hash1 = Hash1()(key) % len;
if (!_bs.test(hash1))
{
return false;
}
size_t hash2 = Hash2()(key) % len;
if (!_bs.test(hash2))
{
return false;
}
size_t hash3 = Hash3()(key) % len;
if (!_bs.test(hash3))
{
return false;
}
// 在 不准确的,存在误判
// 不在 准确的
return true;
}
private:
static const size_t _X = 6;
bitset<N*_X> _bs;
};
void test_bloomfilter1()
{
BloomFilter<100> bs;
bs.set("sort");
bs.set("bloom");
bs.set("hello world hello bit");
bs.set("test");
bs.set("etst");
bs.set("estt");
cout << bs.test("sort") << endl;
cout << bs.test("bloom") << endl;
cout << bs.test("hello world hello bit") << endl;
cout << bs.test("etst") << endl;
cout << bs.test("test") << endl;
cout << bs.test("estt") << endl;
cout << bs.test("ssort") << endl;
cout << bs.test("tors") << endl;
cout << bs.test("ttes") << endl;
}
void test_bloomfilter2()
{
srand(time(0));
const size_t N = 10000;
BloomFilter<N> bf;
std::vector<std::string> v1;
std::string url = "https://www.cnblogs.com/-clq/archive/2012/05/31/2528153.html";
for (size_t i = 0; i < N; ++i)
{
v1.push_back(url + std::to_string(i));
}
for (auto& str : v1)
{
bf.set(str);
}
// v2跟v1是相似字符串集,但是不一样
std::vector<std::string> v2;
for (size_t i = 0; i < N; ++i)
{
std::string url = "https://www.cnblogs.com/-clq/archive/2012/05/31/2528153.html";
url += std::to_string(999999 + i);
v2.push_back(url);
}
size_t n2 = 0;
for (auto& str : v2)
{
if (bf.test(str))
{
++n2;
}
}
cout << "相似字符串误判率:" << (double)n2 / (double)N << endl;
// 不相似字符串集
std::vector<std::string> v3;
for (size_t i = 0; i < N; ++i)
{
string url = "zhihu.com";
//string url = "https://www.cctalk.com/m/statistics/live/16845432622875";
url += std::to_string(i + rand());
v3.push_back(url);
}
size_t n3 = 0;
for (auto& str : v3)
{
if (bf.test(str))
{
++n3;
}
}
cout << "不相似字符串误判率:" << (double)n3 / (double)N << endl;
}
布隆过滤器使用场景是什么?
1、能容忍误判的场景。比如:注册时,快速判断昵称是否使用过。因为昵称在布隆过滤器判断的结果是没有用过就一定是没有用过,布隆过滤器判断结果是用过了则实际上有一定的概率并没有被用过。
2、给两个文件,分别有100亿个query,我们只有1G内存,如何找到两个文件交集?分别给出精确算法和近似算法。
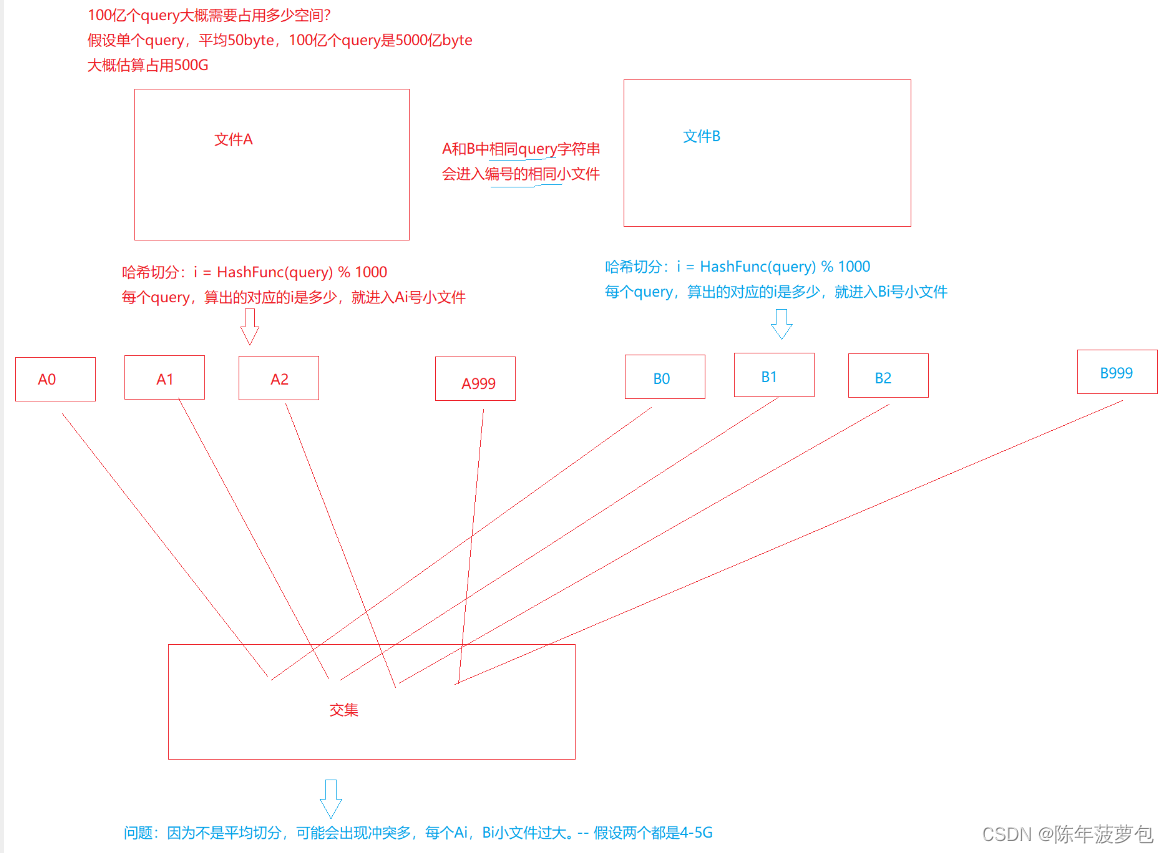
造成上述问题的原因:1、单个文件中,有大量不同的query;2、单个文件中,有某个大量重复的query;

3. 给一个超过100G大小的log file, log中存着IP地址,设计算法找到出现次数最多的IP地址?
如何找到top K的IP?