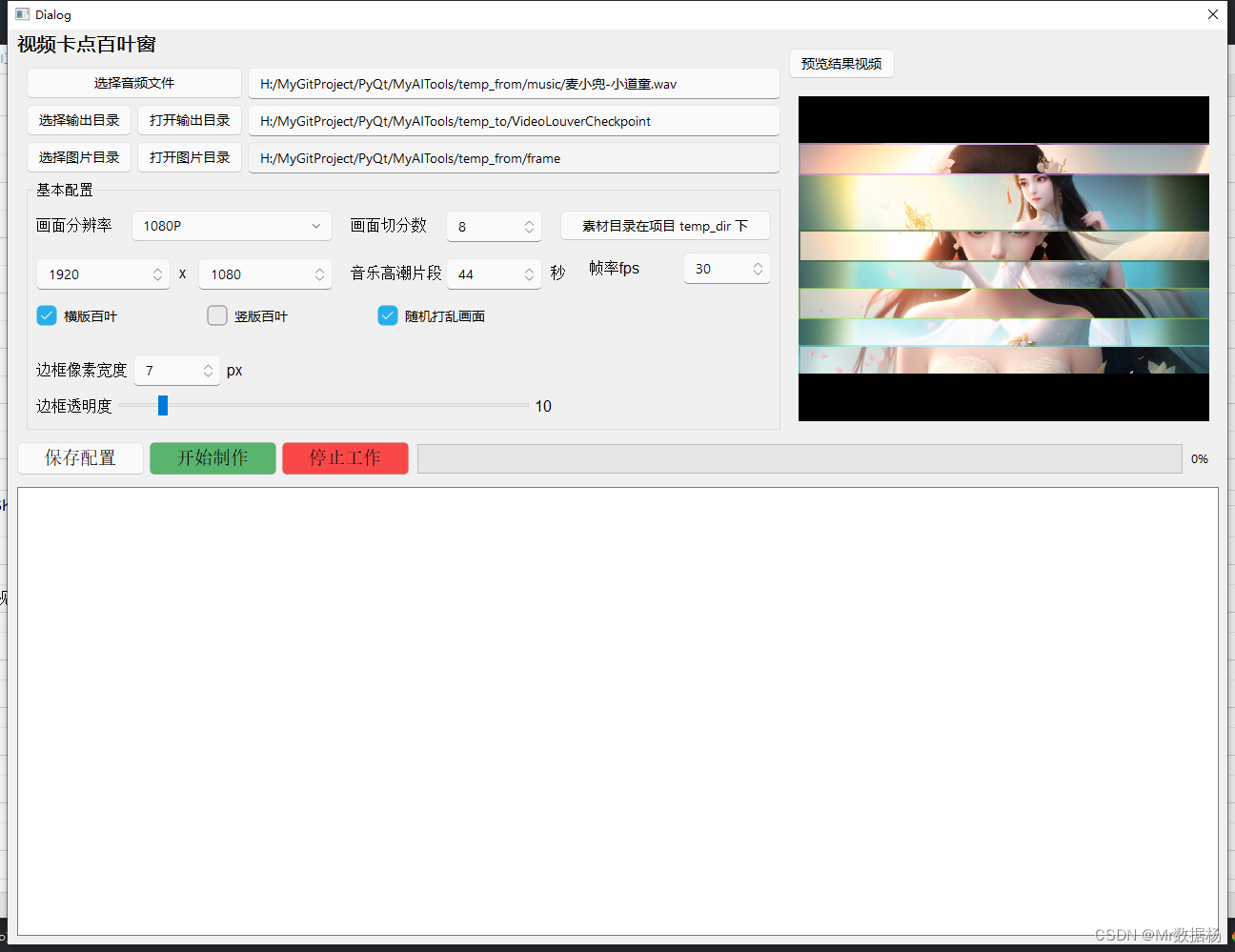
特值法

题干中存在乘除关系，且对应量未知。

例3：甲、乙、丙三个工程队的效率比为6：5：4,现将A、B两项工作量相同的工程交给这三个工程队,甲队负责A工程,乙队负责B工程,丙队参与A工程若干天后转而参与B工程.两项工程同时开工,耗时16天同时结束,问丙队在A工程中参与施工多少天?

A.6 B.7 C.8 D.9

【参考解析】A。合作问题中给出效率之比，可以按照效率之比设特值，故设甲、乙、丙三个工程队的效率为6、5、4，则三个队合作16天，共完成工作量(6+5+4)×16=240个，而A、B两个工程的工作量相等，故A工程的工作量为120，而甲16天一直在A工程，16天共完成6×16=96个工作量，对于A工程中的其余120-96=24个工作均为丙完成，故丙在A共存的天数为24÷4=6天，选择A。

其实这种题还有个更简便的方法，因为甲乙丙的工作时间是相同的，因此效率比等同于工作量之比，现在AB两个工程的工作量相同，消耗的时间也相同，所以我们想办法把丙的4份工作量分给甲的6和乙的5，使甲=乙。为了凑整，都乘以二得到12:10:8，那么把8分成3:5分别分给12和10，正好得到15:15:0。因此丙在A和B那里工作的天数之比是3:5，也就是6天：10天，选A。