NMPC非线性模型预测控制经验分享与代码实例

原本做完本科毕设之后就应该动笔写这一部分，但是做的过程中慢慢意识到自己懂的只是一点点。最近重新接触一些优化相关的问题，希望能够做出我认知之下比较好的解答。本人知识有限，难免写的有问题，希望大家能够指出。

在开始之前，我先抛出两个问题，希望到最后大家能够得到这个问题的答案：

• 什么是NMPC问题？
• 我们如何解决NMPC问题？

1. 线性MPC问题回顾

在上一部分内容中，根据dr_can老师的视频指导，我们了解了模型预测控制的基本理念。模型预测控制在k时刻需要三步：

第一步：估计/测量读取系统的当前状态；

第二步：基于u(k),u(k+1),u(k+2)…u(k+j)进行最优化处理；

第三步：只取u(k)作为系统的控制输入施加到系统上。

在后面的例子中，我们用了一个线性的模型来验证我们的策略。我们将预测区间内的状态写出来，使用二次规划来求解系统的最优值。当时我们定义的系统状态函数是这样的：
$$\dot{X}=AX+BU$$
我们定义的代价函数是这样的：
$$\underset{u_0,\dots ,u_{N-1}}{\min }J=x_N^{\top }F{x}_N+\sum _{k=0}^{N-1}(u_k^{\top }R{u}_k+x_k^{\top }Q{x}_k)$$

2. 问题构建

点进来的朋友可能会要问这样的问题：如果我们的系统模型、我们定义的代价不是上面这样的形式的怎么办？

答：难办。如果我们的形式不是按上面的形式写的话，我们就无法写成上述二次规划(QP)来求解的形式。二次规划的好处在于它可以十分快速地求解出预测控制的全局最优解（即计算得又快又好）。

对于更一般性的情况，系统状态为：
$$\dot{x}=f(x(t),u(t))$$
系统的代价为：
$$\underset{u_0,\dots ,u_{N-1}}{\min }J=l_f(x_N)+\sum _{k=0}^{N-1}l(x_k,u_k)$$
这里的模型和代价可以是非线性的。对于如何求解这样的问题，让我们通过一个例子来理解。

3. 求解示例：倒立摆控制

本文的求解一部分参考了Dr. Li的视频，如果想要了解如何在simulink中实现类似的控制方法，请移步b站或他的github。

本文的求解采用m文件实现，开源代码可参考这里。同时本文使用非线性求解库casadi，如果使用nmpc的话需要在这里安装。

为了能看到控制的效果，这里我选择了一种经典的非线性模型：倒立摆模型(cart-pole)，大概是这个样子：

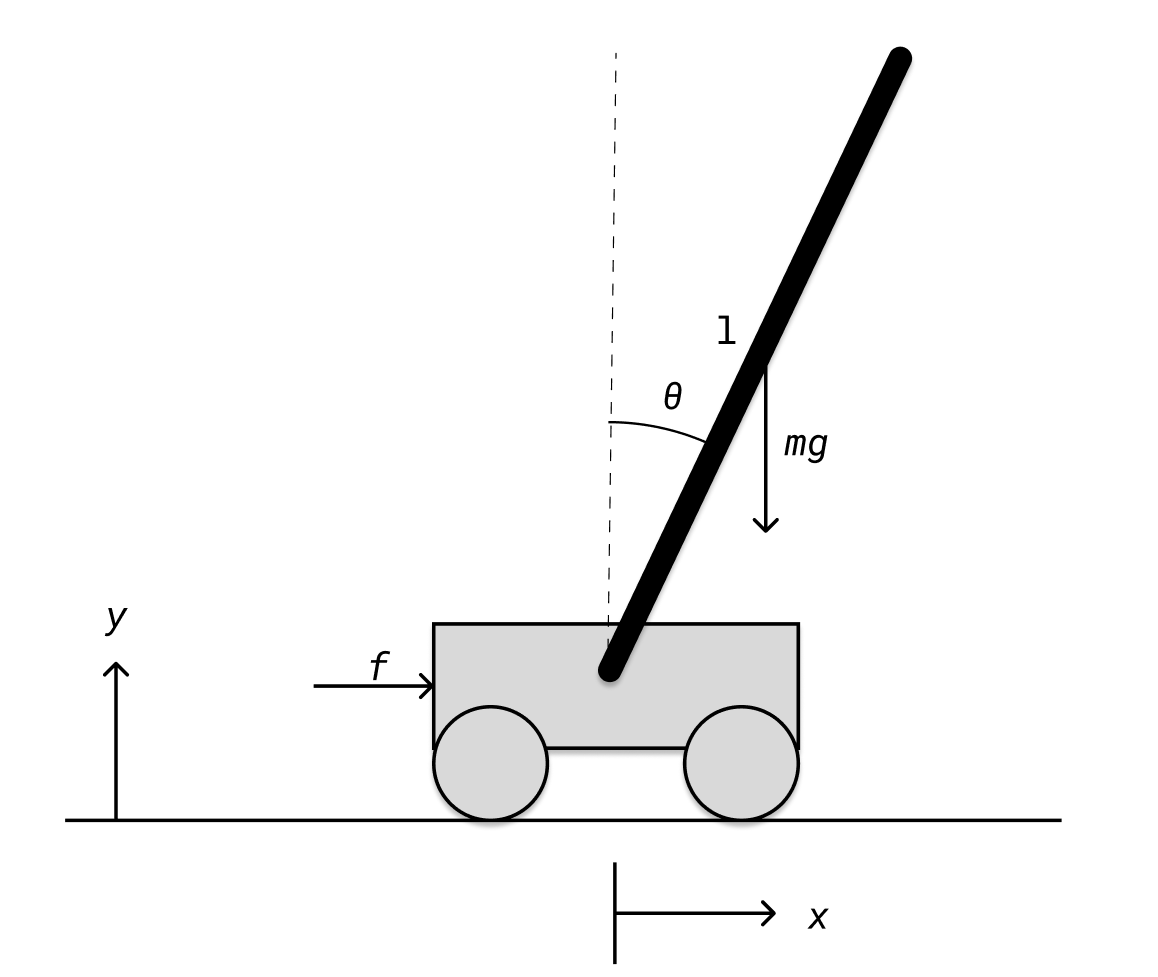
我们状态变量是小车的位移x，杆的角度$\theta$以及它们的导数$\dot{x},\dot{\theta }$，输入为施加在小车上的力$f$。

倒立摆的动力学模型为：
$$\underset{\mathbf{M}(\mathbf{q})}{\underbrace{\left[\begin{array}{cc}{m}_c+m_p& m_{p}L\cos \theta \\ m_{p}L\cos \theta & m_p{L}^2\end{array}\right]}}\underset{\ddot{\mathbf{q}}}{\underbrace{\left[\begin{array}{c}\ddot{x}\\ \ddot{\theta }\end{array}\right]}}+\underset{\mathbf{C}(\mathbf{q},\dot{\mathbf{q}})}{\underbrace{\left[\begin{array}{cc}0& -m_{p}L\sin \theta \dot{\theta }\\ 0& 0\end{array}\right]}}\underset{\dot{\mathbf{q}}}{\underbrace{\left[\begin{array}{c}\dot{x}\\ \dot{\theta }\end{array}\right]}}+\underset{\mathbf{g}(\mathbf{q})}{\underbrace{\left[\begin{array}{c}0\\ -m_{p}gL\sin \theta \end{array}\right]}}=\underset{\mathbf{\tau }}{\underbrace{\left[\begin{array}{c}f\\ 0\end{array}\right]}}$$
其中杆的质量为$m_p$（集中在末端的小球上），车的质量为$m_c$，杆的长度为$L$。注意这是一个非线性的模型，因为M矩阵C矩阵,g矩阵均和系统的状态变量相关。

我们的控制目标是让杆始终保持竖直向上，即$X_d=[x_d,{\theta }_d,{\dot{x}}_d,{\dot{\theta }}_d]=0$

代价函数为：
$$\underset{u_0,\dots ,u_{N-1}}{\min }J=x_N^{\top }F{x}_N+\sum _{k=0}^{N-1}(u_k^{\top }R{u}_k+x_k^{\top }Q{x}_k)$$
其中$x_k=X_k-X_{d,k},u_k=\tau$，接下来，我们来求解这个问题。

4. 求解思路：工作点线性化（LQR，LMPC）

观察上述的问题构建，我们发现系统的动力学是非线性的，但系统的代价函数是线性的，那我们可不可以使用某种方法将系统转化为一个线性化模型，然后用控制线性化模型的方法来处理？

让我们来尝试一下将这个系统在期望位置处进行线性化。我们知道，当$\theta$ 趋近于0时，有$\sin \theta \approx \theta ,\cos \theta \approx 1$，我们将其代入到状态方程中，并忽略项 $m_{p}L\sin \theta {\dot{\theta }}^2$，我们得到系统在工作点$X=[0,0,0,0{]}^{\top }$线性化模型为：
$$\left[\begin{array}{c}\dot{x}\\ \dot{\theta }\\ \ddot{x}\\ \ddot{\theta }\end{array}\right]=\left[\begin{array}{cccc}0& 0& 1& 0\\ 0& 0& 0& 1\\ 0& -m_{p}g/m_c& 0& 0\\ 0& (m_{p}g+m_{c}g)/(m_{C}L)& 0& 0\end{array}\right]\left[\begin{array}{c}x\\ \theta \\ \dot{x}\\ \dot{\theta }\end{array}\right]+\left[\begin{array}{c}0\\ 0\\ 1/m_c\\ -1/m_{c}L\end{array}\right]f$$
对倒立摆进行LQR控制，计算LQR增益(LQR控制这里只计算了一次增益)：

function K = cartPoleLQR(Q, R)
global mc mp l g

A = [0 0 1 0;
    0 0 0 1;
    0 -mp*g/mc 0 0;
    0 (mp*g + mc*g)/(mc*l) 0 0];
B = [0;0;1/mc;-1/(mc*l)];
C = eye(4);
D = 0;

cartpole = ss(A,B,C,D);
K = lqr(cartpole, Q, R);
end

设定初始状态为$[0,\pi /4,0,0{]}^{\top }$，调整Q,R 矩阵参数，得到的结果为：

LQR的优点在于它计算的非常快，每一步只需要乘一次预先计算好的增益即可。

接下来我们用线性MPC的方式进行控制（这样的线性化MPC控制方法也被称为Adaptive MPC，如果为多个工作点线性化并设定不同的QR矩阵，则为Gain-scheduled MPC），线性MPC的部分的代码部分和之前的工作大致相同，主要值得注意的是我添加了输入绝对值小于40的约束，并且MPC跟踪的轨迹用了简单的线性插值。完整代码这里就不贴了，可以移步这里参考

设定同样的初始状态，调整Q,R 矩阵参数，得到的结果为：

看起来似乎MPC控制器的性能并没有比LQR控制器要好，在我个人的认知中，MPC控制器相比于LQR控制器的主要优点在于它可以很好地处理系统约束，比如输入的上下界，限制$x,\theta$的速度等。

线性化模型问题在于我们的线性化模型只能在工作点周围非线性程度不高的区间内近似实际模型。当我们给一些离工作点比较远的初值时，得到的结果是不收敛的。比如我们令系统的初始状态为$[0,\pi /2,0,0{]}^{\top }$，则系统状态不收敛。下图为LMPC得到的结果，系统直接发散了。

5. 求解思路：完全非线性模型 （NMPC）

另一种思路就是不对模型线性化处理，直接用系统的非线性模型来预测系统变化，求解一个非线性优化问题。这样的话求解会比较慢，并且求解出来的值可能不是全局最优的。这里我们调用cassadi来求解这个问题：

function f = cartPoleNMPC(Q, R, q0, qd, p_h, h)

   nmpc = casadi.Opti();
   opts = struct('ipopt', struct('print_level', 0, 'warm_start_init_point', 'yes', 'max_iter', 100));
   nmpc.solver('ipopt', opts);
   X_ref = generateReference(q0,qd',p_h);
   X = nmpc.variable(4,p_h); 
   F = nmpc.variable(1,p_h); 
   nmpc.subject_to ( X(:,1) == q0 );
   for k = 1 : p_h-1
        % dynamics:
        dX = cartPoleDynamics(F(:,k), X(:,k));

        nmpc.subject_to( X(:, k+1) == X(:, k) + h*dX );
        nmpc.subject_to( -40 <= F(:,k) <= 40);
   end
   
    J = 0;
    % cost function
    for k = 1 : p_h
        J = J + (X_ref(:,k) - X(:,k))' * Q ... 
            * (X_ref(:,k) - X(:,k)) + R * F(:,k)^2;
    end
    nmpc.minimize(J);
    solution = nmpc.solve();
    f_all = solution.value(F);
    f = f_all(1);
end

我的电脑每个循环要跑个100ms左右，而我设置的步长是40ms，这算个Bug，也侧面说明了这个算法是真的比较慢。

为了凸显NMPC算法的优势，我们将倒立摆的初值设置为$[0,\pi ,0,0{]}^{\top }$，期望位置不变，得到的结果为：

可以把初始向下的倒立摆摆回来。

6. 完整仿真代码

补充我的完整代码如下：为了显示的好看，我为倒立摆添加了动画效果，并保存为视频。这里无需安装任何依赖。

%% Cartpole nmpc,lmpc,LQR
% dependencies : casadi
% model : cartpole (no friction)
import casadi.*
clear;clc;
format long
%------------------------------config-----------------------------------%
h = 0.04; % step
n = 8; % whole time
N = n/h;  % whole step
t = zeros(1,N); % time vec

% state 
dq = zeros(4,N);
q = zeros(4,N);
% input
u = zeros(1,N);
% initial state
q0 = [0, pi,0,0];
q(:,1) = q0;
% desired state
qd = [0,0,0,0];

% cart-pole dynamics
global mc mp l g
mc = 1; mp = 1; % cart mass, pole mass
l = 1; % pole length
g = 9.8; % gravity

% Linearization of the operating point for LMPC and LQR (> pi/4 will result in failure)
% LQR
% Q = diag([100,10,1, 1 ]); % x q dx dq
% R = 1; % fx
% K = cartPoleLQR(Q, R); % the LQR controller computes the gain only once.

% LMPC
% p_h = 80;
% Q = diag([100,10,1, 1 ]); % x q dx dq
% R = 1; % fx

% NMPC
p_h = 20;
Q = diag([600,1000,100, 40 ]); % x q dx dq
R = 1e-3; % fx
%% loop begin
for i = 1:N-1
%     u(i) = K*(qd'-q(:,i)); % LQR
%     u(i) = cartPoleLMPC(Q, R, q(:,i), qd, p_h, h);
    u(i) = cartPoleNMPC(Q, R, q(:,i), qd, p_h, h); 

    % dynamics (rk4)
    k1 = cartPoleDynamics(u(i), q(:, i));
    k2 = cartPoleDynamics(u(i), q(:, i) + 0.5 * h * k1);
    k3 = cartPoleDynamics(u(i), q(:, i) + 0.5 * h * k2);
    k4 = cartPoleDynamics(u(i), q(:, i) + h * k3);
    
    q(:, i+1) = q(:, i) + (h/6) * (k1 + 2 * k2 + 2 * k3 + k4);
    % update time
    t(i+1) = t(i)+h;
end
%% draw figure
% state fig
figure(1)
plot(t,q(1,:),'-','linewidth',2);hold on;
plot(t,q(2,:),'-','linewidth',2);hold on;title('joint state');grid on;
legend('x','\theta');
% input fig
figure(2)
plot(t,u,'-','linewidth',2);title('input');grid on;
legend('F');
% anime
% video
video = VideoWriter('cartpole.mp4', 'MPEG-4');
video.FrameRate = 1/h; 
open(video);

figure(3)
for i = 1:N
    % pole
    plot([q(1,i) q(1,i)+l*sin(q(2,i))],[0 l*cos(q(2,i))],'LineWidth',4);
    % cart
    width = 0.6;height = 0.3;
    rectangle('Position', [q(1,i)-width/2,-height/2, width, height], 'FaceColor', 'none', 'EdgeColor', 'k','LineWidth',2);
    hold on;
    % ball
    radius = 60;
    scatter(q(1,i)+l*sin(q(2,i)), l*cos(q(2,i)), radius, 'filled', 'r');
    hold off;
    xlim([-2 2]); ylim([-2 2]);  
    xlabel('X'); ylabel('Y');  
    grid on; 
    frame = getframe(gcf);
    writeVideo(video, frame);
end
close(video);

7. 总结

最后，我们来简单回顾一下在倒立摆问题中我们的处理方法。当能够线性化模型、约束、代价函数并且模型非线性程度不强，离工作点比较近时，我们可以采用在工作点线性化的方法来求解。但在远离工作点的位置表现不佳。

直接采用非线性模型去求解的主要难度在于如何保证实时性和解的准确性。具体求解方法仍然是研究热点。在我的领域中，我看到的更多是用iLQR或者SQP方法来求解的。不过这就是题外话了。