题目描述

将一个 二叉搜索树 就地转化为一个 已排序的双向循环链表 。

对于双向循环列表，你可以将左右孩子指针作为双向循环链表的前驱和后继指针，第一个节点的前驱是最后一个节点，最后一个节点的后继是第一个节点。

特别地，我们希望可以 就地 完成转换操作。当转化完成以后，树中节点的左指针需要指向前驱，树中节点的右指针需要指向后继。还需要返回链表中最小元素的指针。

示例 1：

输入：root = [4,2,5,1,3] 

输出：[1,2,3,4,5]

解释：下图显示了转化后的二叉搜索树，实线表示后继关系，虚线表示前驱关系。

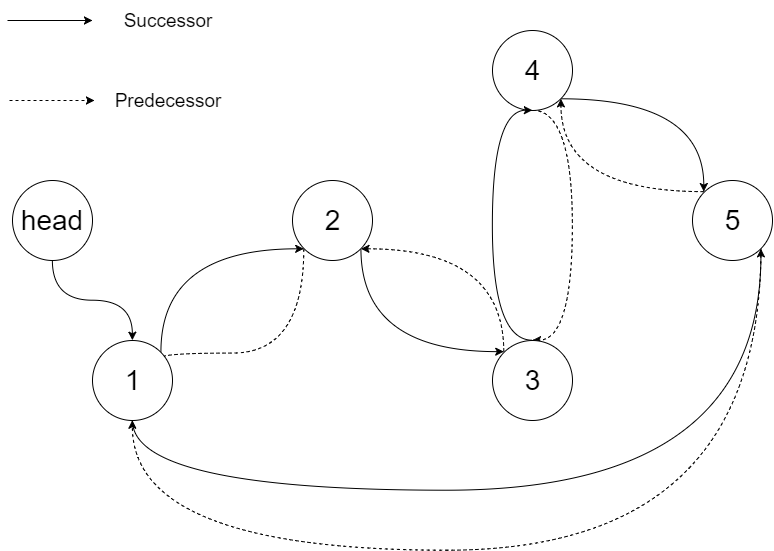
示例 2：

输入：root = [2,1,3]
输出：[1,2,3]

示例 3：

输入：root = []
输出：[]
解释：输入是空树，所以输出也是空链表。

示例 4：

输入：root = [1]
输出：[1]

提示：

• -1000 <= Node.val <= 1000
• Node.left.val < Node.val < Node.right.val
• Node.val 的所有值都是独一无二的
• 0 <= Number of Nodes <= 2000

 

解题思路

我们可以通过递归的方法来解决这个问题。主要思想是：

1. 递归处理左子树，将其转换为一个双向链表。
2. 将当前节点与左子树的链表连接。
3. 递归处理右子树，将其转换为一个双向链表。
4. 将当前节点与右子树的链表连接。
5. 最终将整个链表首尾相连。

具体步骤如下：

1. 递归处理左子树：

   • 如果 root 存在左子树，递归调用 TreeToDoublyList 函数将左子树转换为一个双向链表，并获取该链表的头节点和尾节点。
   • 将左子树链表的尾节点与当前 root 节点连接：左子树的尾节点的右指针指向 root，root 的左指针指向左子树的尾节点。

2. 递归处理右子树：

   • 如果 root 存在右子树，递归调用 TreeToDoublyList 函数将右子树转换为一个双向链表，并获取该链表的头节点和尾节点。
   • 将右子树链表的头节点与当前 root 节点连接：右子树的头节点的左指针指向 root，root 的右指针指向右子树的头节点。

3. 将链表首尾相连：

   • 将整个链表的头节点的左指针指向链表的尾节点，将尾节点的右指针指向链表的头节点，从而形成一个循环双向链表。

4. 返回结果：

   • 递归处理完所有节点后，返回形成的双向链表的头节点。

/*
// Definition for a Node.
class Node {
public:
    int val;
    Node* left;
    Node* right;

    Node() {}

    Node(int _val) {
        val = _val;
        left = NULL;
        right = NULL;
    }

    Node(int _val, Node* _left, Node* _right) {
        val = _val;
        left = _left;
        right = _right;
    }
};
*/

class Solution {
public:
    pair<Node*, Node*> TreeToDoublyList(Node *root) {
        Node *leftHead = root, *leftTail = NULL, *rightHead = NULL, *rightTail = root;
        if (root->left) {
            tie(leftHead, leftTail) = TreeToDoublyList(root->left);
            leftTail->right = root;
            root->left = leftTail;
        }
        if (root->right) {
            tie(rightHead, rightTail) = TreeToDoublyList(root->right);
            rightHead->left = root;
            root->right = rightHead;
        }
        leftHead->left = rightTail;
        rightTail->right = leftHead;
        return {leftHead, rightTail};
    }

    Node* treeToDoublyList(Node* root) {
        return root ? TreeToDoublyList(root).first : NULL;
    }
};