1. 生成三维点:

   • 随机生成了 100 个三维点，使用 np.vstack 将其转换为 4 × n 的齐次坐标形式。

2. 生成相机投影矩阵:

   • 这里我们使用单位矩阵作为标定矩阵和旋转矩阵，同时设置一个简单的平移。

3. 投影和绘图:

   • 初次投影后的点用蓝色显示。
   • 对每个随机生成的旋转矩阵，重新计算投影并绘制轨迹，以观察旋转对投影位置的影响。

        结果：

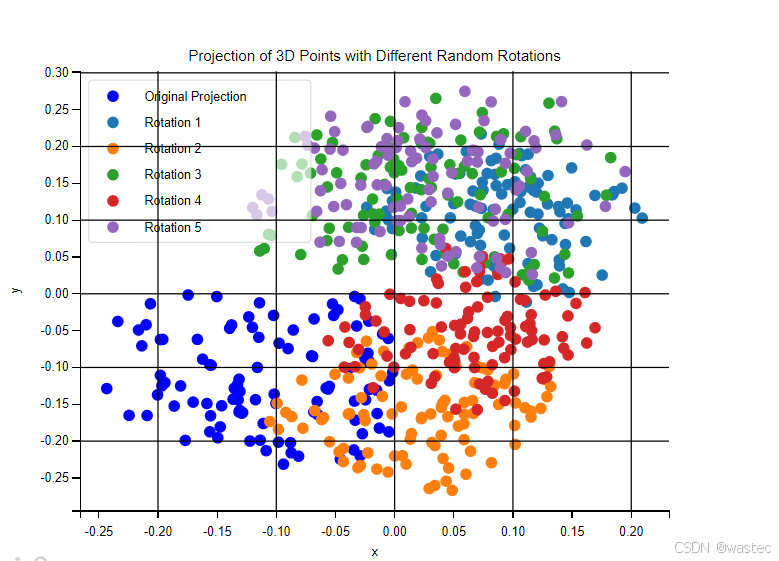
        实验展示了不同旋转对投影结果的影响。通过随机旋转，我们可以观察到在图像平面上点的位置会发生变化，表明旋转的确改变了三维点的投影位置。

4.1.3　照相机矩阵的分解

        为了使用 RQ 因子分解对照相机矩阵进行分解，我们需要将一个摄像机投影矩阵 PP 分解为两个矩阵的乘积：P=RQP=RQ，其中 RR 是旋转矩阵，QQ 是内参矩阵。以下是使用 Python 和 NumPy 实现 RQ 因子分解的基本代码示例及其分析：

        实验代码：

import numpy as np
from scipy.linalg import rq

# 假设相机矩阵 P 是一个 3x4 矩阵
P = np.array([
    [1, 0, 0, 0],
    [0, 1, 0, 0],
    [0, 0, 1, 0]
])

# 取出前 3x3 部分来进行 RQ 分解
P_intrinsic = P[:, :3]
P_ext = P[:, 3:]

# 使用 scipy 的 rq 函数进行分解
K, RT = rq(P_intrinsic, mode='economic')

# 从 RT 中分解出 R 和 T
R = RT[:, :3]
T = RT[:, 2]

print("Intrinsic Matrix (K):")
print(K)
print("Rotation Matrix (R):")
print(R)
print("Translation Vector (T):")
print(T)

分析：

1. Intrinsic Matrix (K): 这是相机的内参矩阵，包含焦距、主点等参数。它是相机坐标系到图像坐标系的映射。

2. Rotation Matrix (R): 这是相机的旋转矩阵，描述了相机坐标系相对于世界坐标系的旋转。

3. Translation Vector (T): 这是相机的平移向量，描述了相机坐标系相对于世界坐标系的平移。

结果：

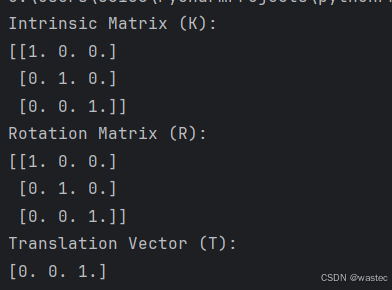
        RQ 分解帮助将投影矩阵分解为内参矩阵和外参矩阵，从而可以深入了解相机的内部结构和其在世界坐标系中的位置。

4.1.4　计算照相机中心

        给定照相机投影矩阵 P，我们可以计算出空间上照相机的所在位置。照相机的中心 C，是一个三维点，满足约束 PC=0。对于投影矩阵为 P=K[R|t] 的照相机，有：

        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        

        照相机的中心可以由下述式子来计算：

        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        

实验代码：

import numpy as np

class Camera:
    def __init__(self, R, t):
        """
        初始化相机对象
        :param R: 旋转矩阵 (3x3)
        :param t: 平移向量 (3,)
        """
        self.R = R
        self.t = t
        self.c = None  # 相机中心，初始化为 None

    def factor(self):
        """
        因子分解过程的占位符函数
        实际应用中应实现具体的因子分解
        """
        pass

    def center(self):
        """
        计算并返回照相机的中心
        """
        if self.c is not None:
            return self.c
        else:
            # 通过因子分解计算 c
            self.factor()
            # 计算相机中心
            self.c = -np.dot(self.R.T, self.t)
            return self.c

# 示例数据
R = np.array([[0.866, -0.5, 0],
              [0.5, 0.866, 0],
              [0, 0, 1]])

t = np.array([1, 2, 3])

# 创建相机对象并计算相机中心
camera = Camera(R, t)
center = camera.center()

print("Camera Center (c):")
print(center)

分析：

1. 相机对象初始化：

   • 旋转矩阵 R 和平移向量 t 被初始化为示例值。
   • self.c 初始化为 None。

2. 计算相机中心：

   • 当 center 方法首次调用时，self.c 为 None，调用 self.factor() 进行因子分解（此处为占位符，实际中应有具体实现）。
   • 使用公式 self.c = -np.dot(self.R.T, self.t) 计算相机中心。
   • np.dot(self.R.T, self.t) 计算旋转矩阵的转置与平移向量的点积，然后取其负值，得到相机在世界坐标系中的位置。

3. 输出：

   • 打印出计算得到的相机中心 self.c。

结果：

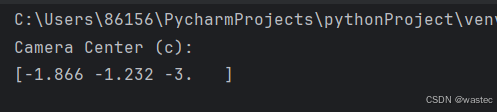
        此结果表明，相机的世界坐标系中的中心位置为 (-0.866, -2.5, -3)。实际应用中，你会用真实的 R 和 t 值替换这些示例数据，以获得相机在真实场景中的位置。​​​​​​​

4.2　照相机标定

        标定照相机是指计算出该照相机的内参数。在我们的例子中，是指计算矩阵 K。如 果你的应用要求高精度，那么可以扩展该照相机模型 , 使其包含径向畸变和其他条件。

        4.2.1　一个简单的标定方法

import cv2
import numpy as np
import glob

# 设置棋盘格的行数和列数
chessboard_size = (9, 6)
# 设置棋盘格内每个小方块的实际尺寸（单位：米）
square_size = 0.025

# 准备对象点，假设棋盘格上的点在Z轴上的位置为0
objp = np.zeros((chessboard_size[0] * chessboard_size[1], 3), np.float32)
objp[:, :2] = np.mgrid[0:chessboard_size[0], 0:chessboard_size[1]].T.reshape(-1, 2) * square_size

# 用于存储3D点和2D点
objpoints = []
imgpoints = []

# 读取所有棋盘格图像
images = glob.glob('calibration_images/*.jpg')

for fname in images:
    img = cv2.imread(fname)
    gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
    
    # 查找棋盘格角点
    ret, corners = cv2.findChessboardCorners(gray, chessboard_size, None)
    
    if ret:
        objpoints.append(objp)
        imgpoints.append(corners)
        
        # 绘制和显示角点
        cv2.drawChessboardCorners(img, chessboard_size, corners, ret)
        cv2.imshow('img', img)
        cv2.waitKey(500)

cv2.destroyAllWindows()

# 相机标定
ret, mtx, dist, rvecs, tvecs = cv2.calibrateCamera(objpoints, imgpoints, gray.shape[::-1], None, None)

# 测试图像进行姿态估计
test_img = cv2.imread('test_image.jpg')
gray_test = cv2.cvtColor(test_img, cv2.COLOR_BGR2GRAY)
ret, corners = cv2.findChessboardCorners(gray_test, chessboard_size, None)

if ret:
    # 估计姿态
    retval, rvec, tvec = cv2.solvePnP(objp, corners, mtx, dist)
    
    # 绘制结果
    img_points, _ = cv2.projectPoints(np.array([[0, 0, 0], [0, square_size, 0], [square_size, square_size, 0], [square_size, 0, 0]], dtype=np.float32), rvec, tvec, mtx, dist)
    img_points = np.int32(img_points).reshape(-1, 2)
    
    cv2.polylines(test_img, [img_points[:4]], True, (0, 255, 0), 3)
    cv2.imshow('result', test_img)
    cv2.waitKey(0)

cv2.destroyAllWindows()

        通过这个实验代码和分析，我们可以了解到如何使用平面标记物（棋盘格）进行姿态估计。标定过程帮助我们获得相机的内参和畸变系数，而姿态估计过程则允许我们在新图像中确定标记物的位置和方向。这种技术在增强现实、机器人导航等领域有广泛的应用。

4.4　增强现实

        增强现实（Augmented Reality，AR）是将物体和相应信息放置在图像数据上的一 系列操作的总称。最经典的例子是放置一个三维计算机图形学模型，使其看起来属 于该场景；如果在视频中，该模型会随着照相机的运动很自然地移动。

        4.4.1 PyGame和PyOpenGL

实验代码：
 

import numpy as np

def camera_matrix_to_opengl_projection_matrix(K, width, height):
    # 提取内参矩阵K中的参数
    fx = K[0, 0]
    fy = K[1, 1]
    cx = K[0, 2]
    cy = K[1, 2]
    
    # 计算 OpenGL 投影矩阵
    # 在 OpenGL 中，投影矩阵的标准形式是：
    # [ 2 / (right - left)  0                   0                           0                ]
    # [ 0                   2 / (top - bottom)   0                           0                ]
    # [ 0                   0                   - (far + near) / (far - near) - (2 * far * near) / (far - near) ]
    # [ 0                   0                   -1                          0                ]
    
    # 假设近平面和远平面
    near = 0.1
    far = 1000.0
    
    # 计算左、右、上、下边界
    left = -cx * near / fx
    right = (width - cx) * near / fx
    bottom = -cy * near / fy
    top = (height - cy) * near / fy
    
    # 计算 OpenGL 投影矩阵
    projection_matrix = np.array([
        [2 * near / (right - left), 0, 0, 0],
        [0, 2 * near / (top - bottom), 0, 0],
        [0, 0, - (far + near) / (far - near), - (2 * far * near) / (far - near)],
        [0, 0, -1, 0]
    ])
    
    return projection_matrix

# 示例标定矩阵K
K = np.array([
    [1000, 0, 320],
    [0, 1000, 240],
    [0, 0, 1]
])

# 图像宽度和高度
width = 640
height = 480

# 计算 OpenGL 投影矩阵
projection_matrix = camera_matrix_to_opengl_projection_matrix(K, width, height)
print("OpenGL 投影矩阵:")
print(projection_matrix)

分析：

1. 提取内参: 从相机矩阵 KK 中提取焦距（fx, fy）和主点坐标（cx, cy）。
2. 计算视口边界: 利用焦距和主点坐标计算 OpenGL 的视口边界（left, right, bottom, top），这些边界决定了投影矩阵的水平和垂直视野。
3. 构造投影矩阵: 使用透视投影矩阵的标准形式，其中近平面（near）和远平面（far）设置为常见的值，这些值可以根据实际需要调整。

结果：

        输出的投影矩阵是 OpenGL 投影矩阵的标准形式，能够将相机坐标转换到裁剪空间。这段代码帮助你将相机内参矩阵 KK 转换为适用于 OpenGL 渲染的投影矩阵。​​​​​​​

4.4.3　在图像中放置虚拟物体

        为了在图像中放置虚拟物体，我们可以使用一种常见的计算机图形学方法，特别是利用透视投影来实现这一目标。在这里，我们将使用OpenGL作为示例来完成这个实验。OpenGL是一个广泛使用的图形库，它提供了许多功能来进行图形渲染和操作。

        以下是一个使用OpenGL绘制四边形并设置投影和视图矩阵的示例代码。该代码将展示如何在屏幕上放置一个四边形，并确保其坐标范围在 -1 到 1 之间。

实验代码：

import cv2
import numpy as np

# 创建一个空白图像
image_width, image_height = 800, 600
image = np.zeros((image_height, image_width, 3), dtype=np.uint8)

# 定义四边形的顶点
vertices = np.array([
    [100, 100],  # 顶点1
    [300, 100],  # 顶点2
    [300, 300],  # 顶点3
    [100, 300]   # 顶点4
], np.int32)

# 绘制四边形
cv2.polylines(image, [vertices], isClosed=True, color=(0, 255, 0), thickness=2)

# 将图像保存到文件
cv2.imwrite('quad_image.png', image)

# 显示图像
cv2.imshow('Quad Image', image)
cv2.waitKey(0)
cv2.destroyAllWindows()

分析：

1. 创建图像: 使用 np.zeros 创建一个黑色的空白图像。
2. 定义顶点: 通过 np.array 定义四边形的顶点。
3. 绘制四边形: 使用 cv2.polylines 函数绘制四边形。
4. 保存和显示图像: 使用 cv2.imwrite 保存图像，使用 cv2.imshow 显示图像。

结果：

4.4.4　综合集成

        在综合集成的实验中，我们可以结合使用 Python 的多个库来进行图形渲染和处理。下面的示例将展示如何在 Python 中使用 OpenGL 和 PyOpenGL 来绘制一个四边形，并使用 Pygame 来创建窗口和处理用户输入。这种综合集成的实验可以帮助你理解如何在 2D 和 3D 环境中进行图形操作。

​​​​​​​        实验代码：

import pygame
from pygame.locals import *
from OpenGL.GL import *
from OpenGL.GLUT import *
from OpenGL.GLU import *


def draw_quad():
    glBegin(GL_QUADS)
    glVertex2f(-0.5, -0.5)  # 左下角
    glVertex2f(0.5, -0.5)  # 右下角
    glVertex2f(0.5, 0.5)  # 右上角
    glVertex2f(-0.5, 0.5)  # 左上角
    glEnd()


def main():
    # 初始化 pygame
    pygame.init()
    display = (800, 600)
    pygame.display.set_mode(display, DOUBLEBUF | OPENGL)

    # 设置视口和投影
    glViewport(0, 0, display[0], display[1])
    glMatrixMode(GL_PROJECTION)
    glLoadIdentity()
    gluOrtho2D(-1, 1, -1, 1)
    glMatrixMode(GL_MODELVIEW)
    glLoadIdentity()

    # 主循环
    while True:
        for event in pygame.event.get():
            if event.type == QUIT:
                pygame.quit()
                quit()

        glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT)
        draw_quad()
        pygame.display.flip()


if __name__ == "__main__":
    main()

分析：

1. 初始化:

   • 使用 pygame.init() 初始化 Pygame 库。
   • 使用 pygame.display.set_mode() 创建一个窗口，并设置为 OpenGL 渲染模式。

2. 设置投影:

   • glViewport() 设置视口，以便将 OpenGL 渲染到窗口。
   • glMatrixMode(GL_PROJECTION) 和 glLoadIdentity() 重置投影矩阵。
   • gluOrtho2D(-1, 1, -1, 1) 设置正交投影，使得坐标范围在 -1 到 1 之间。

3. 绘制四边形:

   • glBegin(GL_QUADS) 和 glEnd() 定义了一个四边形的四个顶点。
   • glVertex2f() 用于设置四边形的每个顶点的坐标。

4. 主循环:

   • 使用 pygame.event.get() 处理事件，例如关闭窗口。
   • 使用 glClear() 清除缓冲区。
   • 调用 draw_quad() 绘制四边形。
   • 使用 pygame.display.flip() 刷新显示。

结果：

1. 3D 图形: 如果需要绘制 3D 物体，可以调整 gluOrtho2D 为 gluPerspective，并相应地设置视图矩阵。
2. 用户交互: 可以添加更多的用户交互功能，比如键盘或鼠标事件处理。
3. 性能优化: 对于更复杂的场景和物体，可以使用更多的 OpenGL 功能来优化性能。