自制深度学习推理框架之表达式层的设计与实现

文章目录

- 一、表达式Expression
- 二、词法解析
- - 2.1 词法定义
  - 2.2 词法解析
- 三、语法解析
- - 3.1 语法树的定义
  - 3.2 语法树构建
  - 3.3 语法树的转换(逆波兰式)
- 四、表达式层
- - 4.1 ExpressionLayer和ExpressionParser类
  - 4.2 表达式层的注册
  - 4.3 表达式层的输入处理
  - 4.4 表达式层的计算过程
- 五、计算图执行函数
- - 5.1 RuntimeGraph::ProbeNextLayer()
  - 5.2 RuntimeGraph::Forward()

一、表达式Expression

在 PNNX 中，Expression 类用于表示和处理计算图中的算子或节点的表达式。这些表达式通常涉及张量之间的运算、函数调用、以及其他数学或逻辑操作。在前面也说过，PNNX 会保留 PyTorch 所定义的表达式。

import torch

def foo(x, y):
    return torch.sqrt((2 * x + y) / 12)

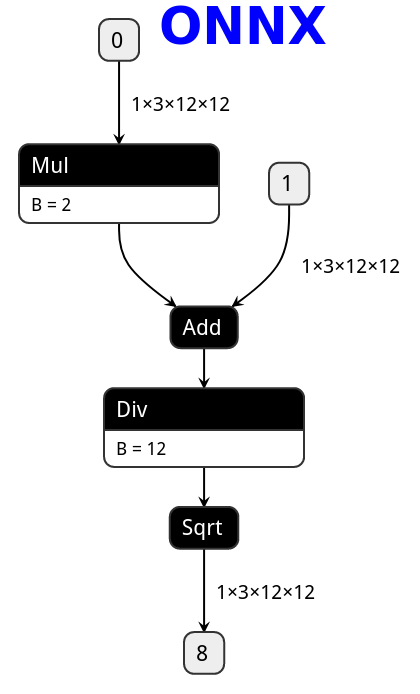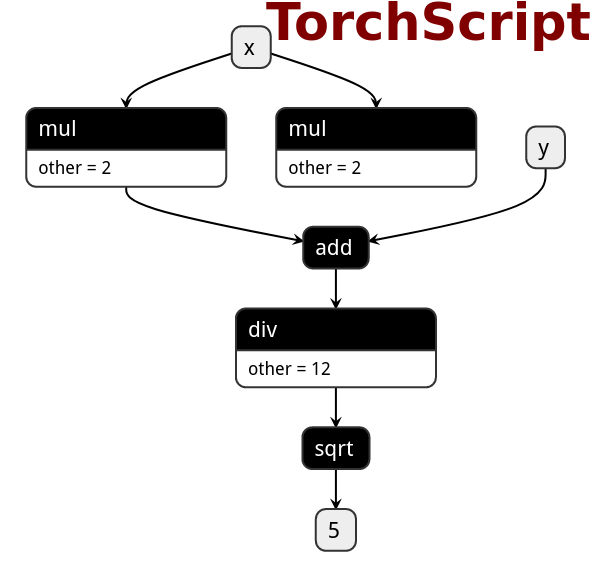在PyTorch中定义表达式在转换为PNNX之后，会保留表达式的整体结构，而不会被拆分成多个小的加减乘除算子。例如表达式sqrt(div(add(mul(@0,2),@1,1),12))不会被拆分为两个mul算子、一个add算子、一个div和sqrt算子，而是会生成一个表达式算子Expression 。

Expression层的主要功能：

表达算子操作：Expression层可以表示各种算子操作，如加法、乘法、卷积等。这些算子通常对应于神经网络中的基本操作。
表达式解析：Expressio层能够解析字符串形式的表达式，将其转换为内部的表达式树或图结构。这种结构可以进一步用于计算、求导或其他符号操作。

在PNNX的**表达式层（Expression Layer）**中，提供了一种计算表达式，该表达式能够在一定程度上折叠计算过程并消除中间变量。例如，在残差结构中的add操作在PNNX中就是一个表达式层。

下面是PNNX中对上述过程的计算表达式表示，其中的@0和@1代表之前提到的计算数RuntimeOperand，用于表示计算表达式中的输入节点。

mul(@2, add(@0, @1));

尽管这个抽象表达式看起来比较简单，但实际上可能存在更为复杂的情况，例如以下的例子。因此，在这种情况下，需要一个强大而可靠的表达式解析和语法树构建功能。

add(add(mul(@0, @1), mul(@2, add(add(add(@0, @2), @3), @4))), @5);

二、词法解析

2.1 词法定义

词法解析的目的是将expr：**add(@0, mul(@1, @2))**拆分为多个Token，拆分后的Token依次为：

Identifier: add
Left bracket: (
Input number: @0
Comma: ,
Identifier: mul
Left bracket: (
Input number: @1
Comma: ,
Input number: @2
Right bracket: )

Token的类型定义如下：

enum class TokenType {
  TokenUnknown = -9,
  TokenInputNumber = -8,    // 数字
  TokenComma = -7,          // 逗号
  TokenAdd = -6,            // 加法
  TokenMul = -5,            // 乘法
  TokenLeftBracket = -4,    // 左括号
  TokenRightBracket = -3,   // 右括号
};

Token的定义如下，包括以下变量：

Token类型，包括add（加法），mul（乘法），bracket（左右括号）等；
Token在原句子中的开始和结束位置，即start_pos和end_pos；

对于表达式add(@0, mul(@1, @2))，可以将它切分为多个Token，其中Token(add)的start_pos为0，end_pos为3。Token(left bracket)的start_pos为3，end_pos为4。Token(@0)的start_pos为4，end_pos为5，以此类推。

// 词语Token
struct Token {
    TokenType token_type = TokenType::TokenUnknown;
    int32_t start_pos = 0; // 词语开始的位置
    int32_t end_pos = 0;   // 词语结束的位置
    Token(TokenType token_type, int32_t start_pos, int32_t end_pos)
        : token_type(token_type), start_pos(start_pos), end_pos(end_pos) {

        }
};

最后，在词法解析结束后，需要将这些 Token（词语）按照它们的出现顺序和层级关系组成一棵语法树。

// 语法树的节点
struct TokenNode {
    int32_t num_index = -1;
    std::shared_ptr<TokenNode> left = nullptr;   // 语法树的左节点
    std::shared_ptr<TokenNode> right = nullptr;  // 语法树的右节点
    TokenNode(int32_t num_index, std::shared_ptr<TokenNode> left,
              std::shared_ptr<TokenNode> right);
    TokenNode() = default;
};

2.2 词法解析

判断句子是否为空

CHECK(!statement_.empty()) << "The input statement is empty!";

移除句子中的空格

statement_.erase(std::remove_if(statement_.begin(), statement_.end(),
                                [](char c) { return std::isspace(c); }),
                 statement_.end());
CHECK(!statement_.empty()) << "The input statement is empty!";

如果表达式层中有表达式为add(@0, @1)，删除其中的空格后就会得到新的表达式add(@0,@1)。

逐个解析句子的字符

for (int32_t i = 0; i < statement_.size();) {
    char c = statement_.at(i);
    if (c == 'a') {  // 判断是否为add
        CHECK(i + 1 < statement_.size() && statement_.at(i + 1) == 'd')
            << "Parse add token failed, illegal character: "
            << statement_.at(i + 1);
        CHECK(i + 2 < statement_.size() && statement_.at(i + 2) == 'd')
            << "Parse add token failed, illegal character: "
            << statement_.at(i + 2);
        Token token(TokenType::TokenAdd, i, i + 3);
        tokens_.push_back(token);
        std::string token_operation =
            std::string(statement_.begin() + i, statement_.begin() + i + 3);
        token_strs_.push_back(token_operation);
        i = i + 3;
    }

假设字符 c 表示当前的字符。如果 c 等于字符 ‘a’，根据词法规定，Token 中以 ‘a’ 开头的情况只有 add。因此，需要判断接下来的两个字符是否分别是 ‘d’ 和 ‘d’。如果不是，则报错。如果是的话，则初始化一个新的 Token，并保存其在表达式中的初始和结束位置。

如果某个字符 c 是 ‘m’，需要判断接下来的字符是否是 ‘u’ 和 ‘l’。如果不满足条件，则说明我们的表达式中出现了词汇表之外的单词（因为词汇表只允许以 ‘m’ 开头的单词是 “mul”）。如果满足条件，同样会初始化一个 Token 实例，并保存该单词的起始和结束位置，以及 Token 的类型。

else if (c == '@') {
    CHECK(i + 1 < statement_.size() && std::isdigit(statement_.at(i + 1)))
        << "Parse number token failed, illegal character: " << c;
    int32_t j = i + 1;
    for (; j < statement_.size(); ++j) {
        if (!std::isdigit(statement_.at(j))) {
            break;
        }
    }
    Token token(TokenType::TokenInputNumber, i, j);
    CHECK(token.start_pos < token.end_pos);
    tokens_.push_back(token);
    std::string token_input_number = std::string(statement_.begin() + i, statement_.begin() + j);
    token_strs_.push_back(token_input_number);
    i = j;

如果第一个字符是 ‘@’，需要读取 ‘@’ 后面的所有数字，例如对于@31231，需要读取@符号之后的所有数字。如果紧跟在 ‘@’ 后面的字符不是数字，则报错。如果是数字，则将这些数字全部读取并组成一个单词（Token）。

else if (c == ',') {
      Token token(TokenType::TokenComma, i, i + 1);
      tokens_.push_back(token);
      std::string token_comma =
          std::string(statement_.begin() + i, statement_.begin() + i + 1);
      token_strs_.push_back(token_comma);
      i += 1;
}

如果第一个字符是’,'逗号，直接读取这个字符作为一个新的Token。

最后，在正确解析和创建这些 Token 后，将它们放入名为 tokens 的数组中，以便进行后续处理。

tokens_.push_back(token);

三、语法解析

3.1 语法树的定义

struct TokenNode {
    int32_t num_index = -1;
    std::shared_ptr<TokenNode> left = nullptr;
    std::shared_ptr<TokenNode> right = nullptr;
    TokenNode(int32_t num_index, std::shared_ptr<TokenNode> left, std::shared_ptr<TokenNode> right);
    TokenNode() = default;
};

在进行语法分析时，可以根据词法分析得到的 token 数组构建抽象语法树。抽象语法树是一个由二叉树组成的结构，每个节点都存储了操作符号或值，并通过左子节点和右子节点与其他节点连接。

对于表达式 “add (@0, @1)”，当 num_index 等于 1 时，表示计算数为 @0；当 num_index 等于 2 时，表示计算数为 @1。若 num_index 为负数，则说明当前节点是一个计算节点，如 “mul” 或 “add” 等。

以下是一个简单的示例：

     add
    /   \
  @0     @1

在这个示例中，根节点是 “add”，左子节点是 “@0”，右子节点是 “@1”。这个抽象语法树表示了一个将 “@0” 和 “@1” 进行相加的表达式。通过将词法分析得到的 token 数组解析并构建抽象语法树，可以进一步对表达式进行语义分析和求值等操作。

3.2 语法树构建

语法解析即解析Token数组，构建抽象语法树，其过程是递归向下的,定义在Generate_函数中。

std::shared_ptr<TokenNode> ExpressionParser::Generate_(int32_t &index) {
    CHECK(index < this->tokens_.size());
    const auto current_token = this->tokens_.at(index);
    CHECK(current_token.token_type == TokenType::TokenInputNumber
          || current_token.token_type == TokenType::TokenAdd || current_token.token_type == TokenType::TokenMul);

这个函数处理的对象是词法解析的Token（单词）数组，因为Generate_是一个递归函数，所以index参数指向Token数组中的当前处理位置.

current_token表示当前被处理的Token，它作为当前递归层的第一个Token，必须是以下类型之一。

TokenInputNumber = 0,
TokenAdd = 2,
TokenMul = 3,

**如果当前Token的类型是输入数字类型，那么会直接返回一个操作数Token作为叶子节点，不再进行下一层递归（如下）。**例如，在表达式add(@0, @1)中的@0和@1被归类为输入数字类型的Token，在解析到这两个Token时会直接创建并返回语法树节点TokenNode。

if (current_token.token_type == TokenType::TokenInputNumber) {
    uint32_t start_pos = current_token.start_pos + 1;
    uint32_t end_pos = current_token.end_pos;
    CHECK(end_pos > start_pos);
    CHECK(end_pos <= this->statement_.length());
    const std::string &str_number =
        std::string(this->statement_.begin() + start_pos, this->statement_.begin() + end_pos);
    return std::make_shared<TokenNode>(std::stoi(str_number), nullptr, nullptr);

}

如果当前Token的类型是mul或者add，需要进行下一层递归来构建对应的左子节点和右子节点。

例如，在处理add(@1,@2)时，遇到add token之后，如下的第一行代码，需要做以下的两步：

首先判断是否存在左括号（left bracket）
然后继续向下递归以获取@1，如下的第14行到17行代码，但由于@1代表的是数字类型，递归后立即返回，如以上代码块中第一行对数字类型Token的处理。

else if (current_token.token_type == TokenType::TokenMul || current_token.token_type == TokenType::TokenAdd) {
    std::shared_ptr<TokenNode> current_node = std::make_shared<TokenNode>();
    current_node->num_index = -int(current_token.token_type);

    index += 1;
    CHECK(index < this->tokens_.size());
    // 判断add之后是否有( left bracket
    CHECK(this->tokens_.at(index).token_type == TokenType::TokenLeftBracket);

    index += 1;
    CHECK(index < this->tokens_.size());
    const auto left_token = this->tokens_.at(index);
    // 判断当前需要处理的left token是不是合法类型
    if (left_token.token_type == TokenType::TokenInputNumber
        || left_token.token_type == TokenType::TokenAdd || left_token.token_type == TokenType::TokenMul) {
        // (之后进行向下递归得到@0
        current_node->left = Generate_(index);
    } else {
        LOG(FATAL) << "Unknown token type: " << int(left_token.token_type);
    }
}

在第17行当左子树递归构建完毕后，将它赋值到add节点的左子树上。对于表达式add(@0, @1)，我们将左子树连接到current_node的left指针中，随后我们开始构建右子树。

	index += 1; 
    // 当前的index指向add(@1,@2)中的逗号
    CHECK(index < this->tokens_.size());
    // 判断是否是逗号
    CHECK(this->tokens_.at(index).token_type == TokenType::TokenComma);

    index += 1;
    CHECK(index < this->tokens_.size());
    // current_node->right = Generate_(index);构建右子树
    const auto right_token = this->tokens_.at(index);
    if (right_token.token_type == TokenType::TokenInputNumber
        || right_token.token_type == TokenType::TokenAdd || right_token.token_type == TokenType::TokenMul) {
      current_node->right = Generate_(index);
    } else {
      LOG(FATAL) << "Unknown token type: " << int(left_token.token_type);
    }

    index += 1;
    CHECK(index < this->tokens_.size());
    CHECK(this->tokens_.at(index).token_type == TokenType::TokenRightBracket);
    return current_node;

随后需要判断@0之后是否存在comma token，如上代码中的第五行。在构建右子树的过程中，对于表达式add(@1,@2)，当index指向逗号的位置时，首先需要判断是否存在逗号。接下来，我们开始构建右子树，在右子树的向下递归分析中，会得到@2作为一个叶子节点。

当右子树构建完成后，将该节点（即Generate_返回的TokenNode，此处为一个叶子节点，其数据为@1）放置于current_node的right指针中。

假设现在表达式层中的表达式是：add(@0,@1)。在词法解析模块中，这个表达式将被构建成一个单词(Token)数组，如以下：

add
(
@0
,
@1
)

在词法解析结束之后，这个表达式将被传递到语法解析模块中，用于构建抽象语法树。Generate_函数首先检查Token数组中的当前单词(Token)是否是以下类型的一种：

CHECK(index < this->tokens_.size());
const auto current_token = this->tokens_.at(index);
CHECK(current_token.token_type == TokenType::TokenInputNumber ||
      current_token.token_type == TokenType::TokenAdd ||
      current_token.token_type == TokenType::TokenMul);

当前的索引为0，表示正在处理Token数组中的"add"单词。针对这个输入，需要判断其后是否是"左括号"来确定其合法性。如果是合法的（add单词之后总存在括号），我们将构建一个左子树。因为对于一个add调用，它的后面总是跟着一个左括号"("，如下方代码的第8行。

else if (current_token.token_type == TokenType::TokenMul ||
         current_token.token_type == TokenType::TokenAdd) {
    std::shared_ptr<TokenNode> current_node = std::make_shared<TokenNode>();
    current_node->num_index = int(current_token.token_type);

    index += 1;
    CHECK(index < this->tokens_.size()) << "Missing left bracket!";
    CHECK(this->tokens_.at(index).token_type == TokenType::TokenLeftBracket);

    index += 1;
    CHECK(index < this->tokens_.size()) << "Missing correspond left token!";
    const auto left_token = this->tokens_.at(index);

在以上代码的第8行中，我们对’add’之后的一个Token进行判断，如果是左括号则匹配成功，开始匹配括号内的元素。对于输入add(@0, @1)，在第10行中，当对索引进行+1操作后，我们需要开始解析括号内左侧的元素left_token.

随后开始递归构建表达式的左子树：

if (left_token.token_type == TokenType::TokenInputNumber ||
    left_token.token_type == TokenType::TokenAdd ||
    left_token.token_type == TokenType::TokenMul) {
    current_node->left = Generate_(index);
}

对于当前的例子，当前索引(index)指向的单词是@0。在这种情况下，由于索引指向的位置是一个输入数字@0(TokenType::TokenInputNumber)的类型，所以该节点进入递归调用后将直接返回。

根据前文给出的例子，add的左子树构建完毕后，下一步需要判断中add(@0,@1)的@0之后是否存在逗号

index += 1;
CHECK(index < this->tokens_.size()) << "Missing comma!";
CHECK(this->tokens_.at(index).token_type == TokenType::TokenComma);

接下来，要为如上的二叉树构建右子树：

const auto right_token = this->tokens_.at(index);
if (right_token.token_type == TokenType::TokenInputNumber ||
    right_token.token_type == TokenType::TokenAdd ||
    right_token.token_type == TokenType::TokenMul) {
    current_node->right = Generate_(index);
} else {
    LOG(FATAL) << "Unknown token type: " << int(right_token.token_type);
}

同样，由于当前索引(index)指向的位置是@1，它是一个输入数据类型，所以该节点在进入递归调用后将直接返回，并成为add节点的右子树，如下方代码所示。

std::shared_ptr<TokenNode> ExpressionParser::Generate_(int32_t &index) {
    CHECK(index < this->tokens_.size());
    ...
    ...
    如果是Input Number就直接返回

    if (current_token.token_type == TokenType::TokenInputNumber) {
        uint32_t start_pos = current_token.start_pos + 1;
        uint32_t end_pos = current_token.end_pos;
        CHECK(end_pos > start_pos);
        CHECK(end_pos <= this->statement_.length());
        const std::string &str_number =
            std::string(this->statement_.begin() + start_pos, this->statement_.begin() + end_pos);
        return std::make_shared<TokenNode>(std::stoi(str_number), nullptr, nullptr);

    }
}

如果现在有一个表达式add(mul(@0,@1),@2)，在词法解析中，它将被分割成以下的数个单词组成的数组：

add
left bracket
mul
left bracket
@0
comma
@1
right bracket
comma
@2
right bracket

当以上的数组被输入到语法解析中后，index的值等于0。随后判断index指向位置的单词类型是否符合要求。

CHECK(current_token.token_type == TokenType::TokenInputNumber ||
      current_token.token_type == TokenType::TokenAdd ||
      current_token.token_type == TokenType::TokenMul);

如果该表达式的第一个单词是"add"，那么我们就像之前的例子一样，将它作为二叉树的左子树进行构建。

if (left_token.token_type == TokenType::TokenInputNumber ||
    left_token.token_type == TokenType::TokenAdd ||
    left_token.token_type == TokenType::TokenMul) {
    current_node->left = Generate_(index);

已知表达式为add(mul(@0,@1),@2)，在处理完这个表达式的左括号之后，当前指向的标记是"mul"，它不属于输入参数类型。因此，在调用Generate_函数时，我们将对"mul"子表达式进行递归分析。

对"mul"子表达式解析的方式和对add(@0,@1)解析的方式相同，"mul"子表达式的分析结果如下图所示：

在子表达式的解析完成并返回后，我们将这颗子树插入到当前节点的左指针上**(current_node->left = Generate_(index))**

随后我们开始解析add(mul(@0,@1),@2)表达式中@2以及其之后的部分作为add的右子树。

if (right_token.token_type == TokenType::TokenInputNumber ||
    right_token.token_type == TokenType::TokenAdd ||
    right_token.token_type == TokenType::TokenMul) {
    current_node->right = Generate_(index);
} else {
    LOG(FATAL) << "Unknown token type: " << int(right_token.token_type);
}

在第4行调用Generate_之后，由于@2是一个输入数类型，不再进行递归分析，所以它将被直接返回并赋值给current_node->right。

std::shared_ptr<TokenNode> ExpressionParser::Generate_(int32_t &index) {
    CHECK(index < this->tokens_.size());
    ...
    ...
    如果是Input Number就直接返回

    if (current_token.token_type == TokenType::TokenInputNumber) {
        uint32_t start_pos = current_token.start_pos + 1;
        uint32_t end_pos = current_token.end_pos;
        CHECK(end_pos > start_pos);
        CHECK(end_pos <= this->statement_.length());
        const std::string &str_number =
            std::string(this->statement_.begin() + start_pos, this->statement_.begin() + end_pos);
        return std::make_shared<TokenNode>(std::stoi(str_number), nullptr, nullptr);

    }
}

3.3 语法树的转换(逆波兰式)

以一个简单的例子来说明，对于计算式add(@0,@1)，首先遇到的节点是add，但在遇到add时缺少进行计算所需的具体数据@0和@1。

**因此，还需要进行逆波兰转换，将操作数放在前面，计算放在后面。**该转换的实现非常简单，只需对原有的二叉树进行后续遍历即可：

void ReversePolish(const std::shared_ptr<TokenNode> &root_node,
                   std::vector<std::shared_ptr<TokenNode>> &reverse_polish) {
    if (root_node != nullptr) {
        ReversePolish(root_node->left, reverse_polish);
        ReversePolish(root_node->right, reverse_polish);
        reverse_polish.push_back(root_node);
    }
}

逆波兰式化后的表达如下：

对于 add (@0,@1)，逆波兰式为：@0,@1,add

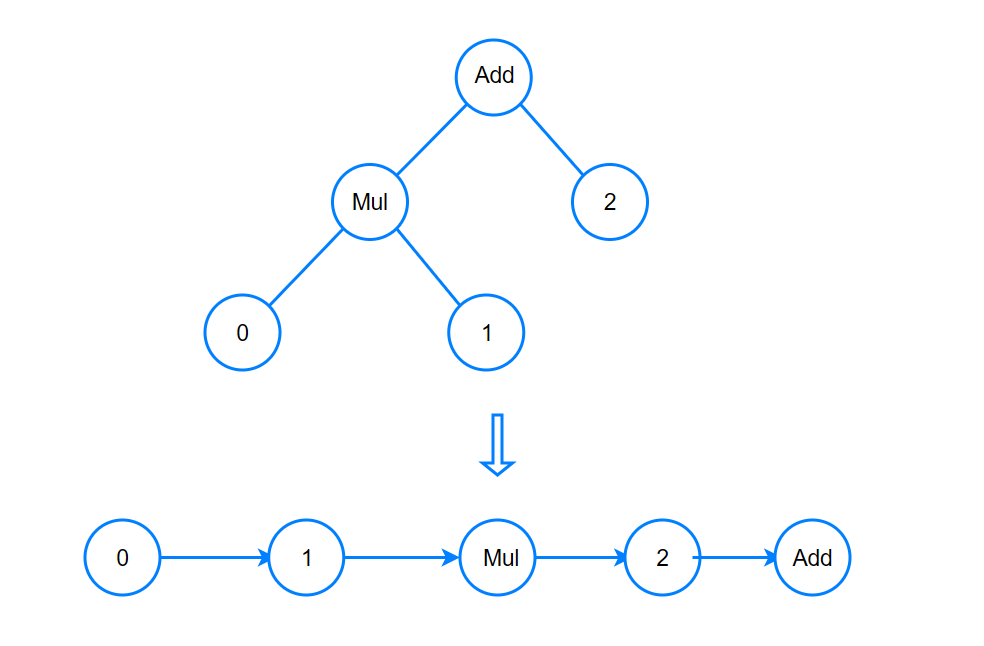
对于 add(mul(@0,@1),@2)，逆波兰式为：@0,@1,mul,@2,add

通过逆波兰转换，可以将原式转换为计算式的输入数放在前面，操作符号放在后面的形式。逆波兰式的特点是消除了括号的需求，使得计算顺序更加清晰和直观。

小节：

经过这样的转换，可以确保在每次遇到计算节点时所需的操作数已经准备就绪。

首先，传入一个表达式字符串，例如add(mul(@0,@1),@2)
接下来，对add(mul(@0,@1),@2)进行词法分析，将其拆分为多个tokens，在拆分过程中需要进行词法校验。
然后，根据已知的tokens数组，通过递归向下遍历进行语法分析，从而得到相应的计算二叉树。计算二叉树的各个节点可以是add、mul或者@0、@1等。
最后，对计算二叉树进行逆波兰变换(后续遍历)，得到的逆波兰式如下：@0、@1、mul、@2、add。

四、表达式层

4.1 ExpressionLayer和ExpressionParser类

class ExpressionLayer : public NonParamLayer {
 public:
  explicit ExpressionLayer( std::string statement);

  InferStatus Forward(
      const std::vector<std::shared_ptr<Tensor<float>>>& inputs,
      std::vector<std::shared_ptr<Tensor<float>>>& outputs) override;

  static ParseParameterAttrStatus GetInstance(
      const std::shared_ptr<RuntimeOperator>& op,
      std::shared_ptr<Layer>& expression_layer);

 private:
  std::string statement_;
  std::unique_ptr<ExpressionParser> parser_;
};

在表达式层面有两个类内变量：

statement_:需要解析的表达式
parser_: 解析器，用于词法分析和语法分析的 ExpressionParser，解析表达式statement_

ExpressionParser类定义在include/parser/parse_expression.hpp

class ExpressionParser {
 public:
  explicit ExpressionParser(std::string statement)
      : statement_(std::move(statement)) {}
  /**
   * 词法分析
   * @param retokenize 是否需要重新进行语法分析
   */
  void Tokenizer(bool retokenize = false);
    
    /**
   * 语法分析
   * @return 生成的语法树
   */
  std::vector<std::shared_ptr<TokenNode>> Generate();
  ...
  ...
 private:
  std::shared_ptr<TokenNode> Generate_(int32_t& index);
  // 被分割的词语数组
  std::vector<Token> tokens_;
  // 被分割的字符串数组
  std::vector<std::string> token_strs_;
  // 待分割的表达式
  std::string statement_;
};

主要负责将输入的表达式字符串转换成一种中间表示形式，通常是逆波兰表示法或抽象语法树（AST）。这个类通常包括：

Tokenizer: 将表达式字符串拆分成 token。
Generate: 解析这些 tokens，构建树结构或其他中间表示形式。
生成逆波兰表示法或抽象语法树: 供其他部分使用。

在ExpressionParser中，，Tokenizer用于将表达式分割为多个单词，例如将add(@0,@1)分割为以下的几个单词：

add
left bracket
input number(@0)
comma
…

ExpressionParser生成语法树Generate函数：

std::vector<std::shared_ptr<TokenNode>> ExpressionParser::Generate() {
  if (this->tokens_.empty()) {
    this->Tokenizer(true);
  }
  int index = 0;
  // 构建语法树
  std::shared_ptr<TokenNode> root = Generate_(index);
  CHECK(root != nullptr);
  CHECK(index == tokens_.size() - 1);

  // 转逆波兰式,之后转移到expression中
  std::vector<std::shared_ptr<TokenNode>> reverse_polish;
  ReversePolish(root, reverse_polish);

  return reverse_polish;
}

在以上的代码中，首先调用 Generate_ 方法。该方法通过对 tokens 数组进行语法分析，生成一棵抽象语法树。然后对这棵抽象语法树进行逆波兰排序，得到最终的执行序列。

4.2 表达式层的注册

LayerRegistererWrapper用于将 GetInstance方法与 “pnnx.Expression” 字符串进行绑定，使得运行时系统能够通过 “pnnx.Expression” 创建 ExpressionLayer实例，将其注册到推理框架中，推理框架才能够使用自定义的表达式层进行计算

LayerRegistererWrapper kExpressionGetInstance("pnnx.Expression",
                                              ExpressionLayer::GetInstance);

初始化过程如下：

ParseParameterAttrStatus ExpressionLayer::GetInstance(
    const std::shared_ptr<RuntimeOperator>& op,
    std::shared_ptr<Layer>& expression_layer) {
  
  // 检查传入的 RuntimeOperator 对象指针是否为空
  CHECK(op != nullptr) << "Expression operator is nullptr";

  // 获取 RuntimeOperator 的参数集合
  const auto& params = op->params;

  // 确认参数中包含 "expr" 键
  if (params.find("expr") == params.end()) {return ParseParameterAttrStatus::kParameterMissingExpr;}

  // 将 "expr" 参数转换为 RuntimeParameterString 类型
  auto statement_param = std::dynamic_pointer_cast<RuntimeParameterString>(params.at("expr"));

  // 如果转换失败，则记录错误并返回参数缺失状态
  if (statement_param == nullptr) {LOG(ERROR) << "Can not find the expression parameter";
    return ParseParameterAttrStatus::kParameterMissingExpr;}

  // 检查参数的类型是否为字符串
  if (statement_param->type != RuntimeParameterType::kParameterString) {
    LOG(ERROR) << "The expression parameter should be of type string";
    return ParseParameterAttrStatus::kParameterMissingExpr;
  }

  // 使用提取到的表达式字符串创建 ExpressionLayer 实例
  expression_layer = std::make_shared<ExpressionLayer>(statement_param->value);

  // 返回成功状态
  return ParseParameterAttrStatus::kParameterAttrParseSuccess;
}

在以上的代码中 statement_param是从PNNX中提取表达式字符串expr，然后使用该字符串来实例化算子。

4.3 表达式层的输入处理

在Expression Layer的Forward函数输入中，也就是在下面这个数组中，多个输入依次排布：

const std::vector<std::shared_ptr<Tensor<float>>>& inputs

如果batch_size的大小为4，那么input1中的元素数量为4，input2的元素数量也为4。input1中的数据都来源于同一批次的操作数1（operand 1），input2中的数据都来源于同一批次的操作数2（operand 2）。其中，input1中的4(batch size = 4)个元素都是来自于操作数1，而input2中的4(batch size = 4)个元素都是来自于操作数2，它们在inputs数组参数中依次排列，如下图所示：

对于两个输入操作数

已知有如上的数据存储排布, 下面将讨论如何根据现有的数据完成add(@0,@1)计算. 可以看到每一次计算的时候, 都以此从input1和input2中取得一个数据进行加法操作, 并存放在对应的输出位置.

对于三个输入操作数

下图的例子展示了对于三个输入,mul(add(@0,@1),@2)的情况:

每次计算的时候依次从input1, input2和input3中取出数据, 并作出相应的运算, 并将结果数据存放于对应的output中。我们简单说明一下：

$output_1=(input_1+input_5)\times input_9$ ，对于第一个输出数据，我们先从取出第一组输入（@0）中第一个输入数据 $input_1$ ，再从第二组输入（@1）中取得第一个输入数据 $input_5$ ，最后再从第三组输入（@2）中取得第一个输入数据 $input_9$ .
$output_2=(input_2+input_6)\times input_{10}$ ，对于第一个输出数据，我们先从取出第一组输入（@0）中第一个输入数据 $input_2$ ，再从第二组输入（@1）中取得第一个输入数据 $input_6$ ，最后再从第三组输入（@2）中取得第一个输入数据 $input_{10}$ .
$output_3=(input_3+input_7)\times input_{11}$ ，对于第一个输出数据，我们先从取出第一组输入（@0）中第一个输入数据 $input_3$ ，再从第二组输入（@1）中取得第一个输入数据 $input_7$ ，最后再从第三组输入（@2）中取得第一个输入数据 $input_{11}$ .
$output_4$ 同理。

4.4 表达式层的计算过程

表达式层同样继承于算子的父类Layer，并重写其中的Forward方法。在Forward方法中，定义了表达式层的计算逻辑，即数据结构中逆波兰式的计算。

假设现在有一个计算式为add(mul(@0,@1),@2)，通过抽象语法树构建和逆波兰转换，得到了以下序列：@0、@1、mul、@2、add。

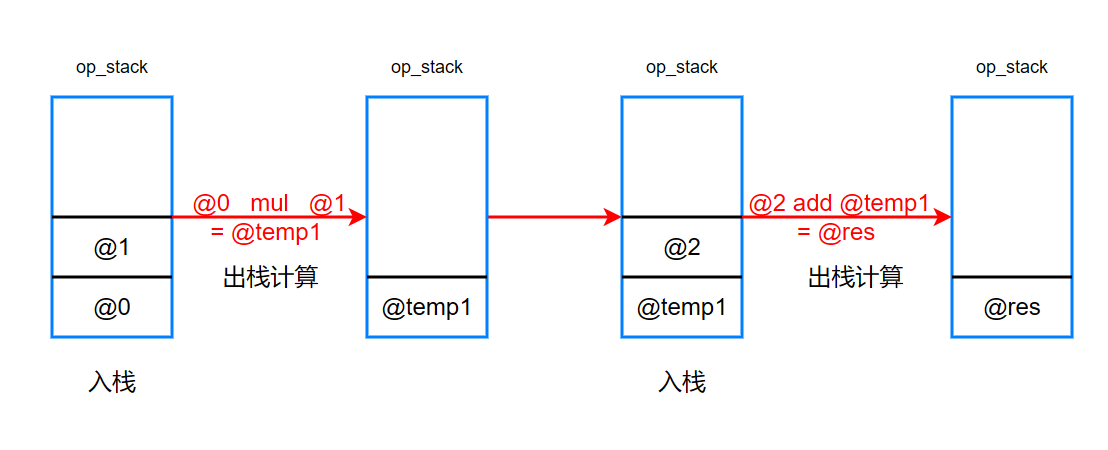
在Forward函数中，定义了一个栈式计算模块，并维护了一个输入数栈。输入数栈是一个先进后出的数据结构，用于存放表达式中的输入数。

对于给定的表达式，例如add(mul(@0,@1),@2) --> (@0 @1 mul @2 add)，将前两个输入数依次压入输入数栈中。在序列中的下一个节点是mul，它的作用是将两个输入数相乘，因此，需要从输入数栈中顺序地弹出两个输入数进行相乘操作。通过该操作，得到一个中间结果@tmp1，需要将这个中间结果存放到输入数栈中，以便供后续步骤处理。

在序列中的下一个节点是@2，是一个输入操作数，将它存放到输入数栈中。在序列中的最后一个节点是add，它是一个加法节点，需要两个输入数据。因此，它会将栈中的@2和@tmp1全部弹出，进行加法操作，得到整个计算序列最后的结果。

代码实现如下：

if (token_node->num_index >= 0) {
    // process operator
    uint32_t start_pos = token_node->num_index * batch_size;
    std::vector<std::shared_ptr<Tensor<float>>> input_token_nodes;
    for (uint32_t i = 0; i < batch_size; ++i) {
        CHECK(i + start_pos < inputs.size())
            << "The " << i
            << "th operand doesn't have appropriate number of tensors";
        input_token_nodes.push_back(inputs.at(i + start_pos));
    }
    op_stack.push(input_token_nodes);
}

根据输入的逆波兰式@0,@1,add，遇到的第一个节点是操作数是@0，所以栈op_stack内的内存布局如下：

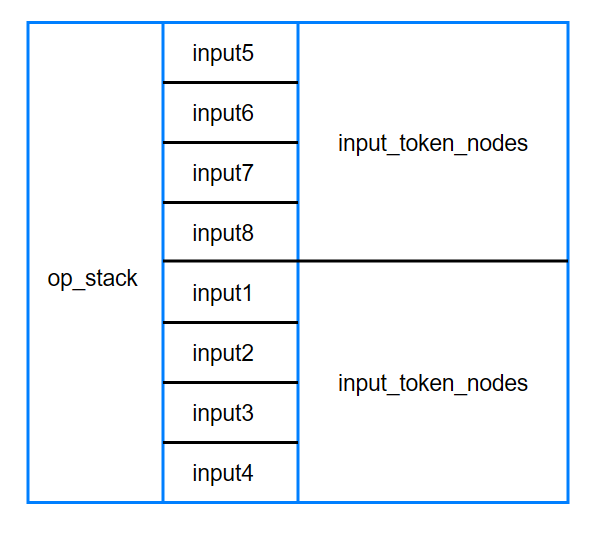
当按顺序遇到第二个节点（op）时，也就是操作数@1时，将从inputs中读取操作数并将其存放到input_token_nodes中。然后，将input_token_nodes这一批次的数据放入栈中。

运算符的代码处理：

const int32_t op = token_node->num_index;
...
std::vector<std::shared_ptr<Tensor<float>>> input_node1 = op_stack.top();
...
...
op_stack.pop();

std::vector<std::shared_ptr<Tensor<float>>> input_node2 = op_stack.top();
CHECK(input_node2.size() == batch_size)
    << "The second operand doesn't have appropriate number of tensors, "
    "which need "
    << batch_size;
op_stack.pop();

当节点（op）类型为操作符号时（也就是num_index小于0的时候），首先从栈（op_stack）中弹出两个批次的操作数。对于给定情况，input_node1存放的是input1至input4，而input_node2存放的是input5至input8。

std::vector<std::shared_ptr<Tensor<float>>> output_token_nodes(
    batch_size);

for (uint32_t i = 0; i < batch_size; ++i) {
    // do execution
    if (op == int(TokenType::TokenAdd)) {
        output_token_nodes.at(i) =
            TensorElementAdd(input_node1.at(i), input_node2.at(i));
    } else if (op == int(TokenType::TokenMul)) {
        output_token_nodes.at(i) =
            TensorElementMultiply(input_node1.at(i), input_node2.at(i));
    } else {
        LOG(FATAL) << "Unknown operator type: " << op;
    }
}
op_stack.push(output_token_nodes);

在获取大小为batch_size的input_node1和input_node2后，流程将在for(int i = 0...batch_size)循环中对这两个输入进行两两操作（input1+input5, input2+input6），具体的操作类型定义于当前的op中。最后，我们将计算得到的结果放入输入数栈op_stack中。

五、计算图执行函数

在完成计算图所有算子的注册后，还需要对计算图中的算子按照拓扑排序依次计算得到推理结果。这里主要涉及RuntimeGraph类中的ProbeNextLayer()函数和Forward()函数。

5.1 RuntimeGraph::ProbeNextLayer()

ProbeNextLayer函数实现了一个关键的图结构操作：确保在执行前向计算时，当前层的输出数据能够正确地传递到依赖该输出的下一层节点。

void RuntimeGraph::ProbeNextLayer(
    const std::shared_ptr<RuntimeOperator> &current_op,  // 表示当前的算子
    // 当前算子的输出，需要把当前算子的输出赋值到它后继节点的输入中
    const std::vector<std::shared_ptr<Tensor<float>>> &layer_output_datas) {
    // 当前节点的后继节点集合
    const auto &next_ops = current_op->output_operators;
  
   // 对所有后继节点进行遍历
   for (const auto &[_, next_rt_operator] : next_ops) {
     // 得到后继节点的输入操作数集合
     const auto &next_input_operands = next_rt_operator->input_operands;
     // 检查当前操作符的输出是否作为后继节点的输入
     if (next_input_operands.find(current_op->name) != next_input_operands.end()) {
      /**
       * next_input_operands:
       * {
       *    输入1 -- current_op.name: current_op对应的输出空间
       *    输入2 -- other_op.name: other_op对应的输出空间
       * }
       */
      // 得到后继节点的关于 current_op 输出的输入张量空间 next_input_datas
      std::vector<std::shared_ptr<ftensor>> &next_input_datas =
          next_input_operands.at(current_op->name)->datas;
      
      // 确保后继节点的输入空间大小与当前操作符的输出空间大小一致
      CHECK(next_input_datas.size() == layer_output_datas.size());
      、
      // 将当前操作符的输出数据赋值到后继节点的输入数据空间中
      for (int i = 0; i < next_input_datas.size(); ++i) {
        next_input_datas.at(i) = layer_output_datas.at(i);
      }
    }
  }
}

在ProbeNextLayer函数中，对当前节点的所有后继节点进行依次的遍历，并将当前节点的输出赋值给后继节点的输入。该过程的三个主要步骤：

遍历后继节点：
- 函数首先获取当前节点 (current_op) 的所有后继节点 (next_ops)。
- 然后，遍历每一个后继节点 (next_rt_operator)。
识别输入输出关系：
- 对于每一个后继节点，函数会识别它的输入张量空间 (next_input_operands)。
- 具体来说，它会寻找与当前节点 (current_op) 对应的输入张量空间，因为每个后继节点可能从多个前驱节点获取输入。
数据赋值：
- 一旦找到对应的输入张量空间 (next_input_datas)，函数会将当前节点 (current_op) 的输出数据 (layer_output_datas) 赋值给后继节点的相应输入张量。

5.2 RuntimeGraph::Forward()

在前面已经详细讲解了模型中所有算子的执行顺序排序，排序的顺序也称为拓扑序。通过对模型中的所有算子进行拓扑排序，可以得到一个算子序列 topo_operators_。因此在执行函数 Forward 时，只需按照顺序依次执行算子序列 (topo_operators) 中每个算子的 Forward 方法即可，因为每个算子（Layer）的具体计算逻辑都实现在它重载的 Forward 方法中。

std::vector<std::shared_ptr<Tensor<float>>> RuntimeGraph::Forward(
        const std::vector<std::shared_ptr<Tensor<float>>>& inputs, bool debug) {
	......
    for (const auto& op : topo_operators_) { op->has_forward = false; } // 重置每个操作符的前向计算标记

    // 遍历按拓扑排序的操作符队列，逐一执行前向计算
    for (const auto& current_op : topo_operators_) {
        // 如果当前操作符是输入节点（pnnx.Input）
        if (current_op->type == "pnnx.Input") {
            current_op->has_forward = true;
            ProbeNextLayer(current_op, inputs);  // 将输入数据传递到下一层
        }
        else if (current_op->type == "pnnx.Output") { // 如果当前操作符是输出节点（pnnx.Output）
            current_op->has_forward = true;
            // 确保输出节点只有一个输入操作数
            CHECK(current_op->input_operands_seq.size() == 1);
            // 将输入操作数设置为输出操作数
            current_op->output_operands = current_op->input_operands_seq.front();
        }
        else {  // 如果当前操作符是普通的计算层
            // 执行当前操作符的前向计算
            InferStatus status = current_op->layer->Forward();
            // 检查前向计算是否成功
            CHECK(status == InferStatus::kInferSuccess) << current_op->layer->layer_name()
                            << " layer forward failed, error code: " << int(status);
            current_op->has_forward = true;
            // 将计算结果传递到下一层
            ProbeNextLayer(current_op, current_op->output_operands->datas);
        }
    }

	.......
    // 获取最终的输出操作数，并返回其数据
    if (operators_maps_.find(output_name_) != operators_maps_.end()) {
        const auto& output_op = operators_maps_.at(output_name_);
        CHECK(output_op->output_operands != nullptr)<< "Output from " << output_op->name << " is empty";
        const auto& output_operand = output_op->output_operands;
        return output_operand->datas;
    } 
    else {
        LOG(FATAL) << "Can not find the output operator " << output_name_;
        return std::vector<std::shared_ptr<Tensor<float>>>{};
    }
}

RuntimeGraph::Forward函数的主要任务是根据拓扑排序顺序依次执行图中的所有操作符的前向计算，最终生成并返回计算结果。

在算子执行的阶段，依次取出topo_operators数组中的所有算子，并调用它们的Forward方法。在遍历执行的循环内，可以将算子分为三类：输入类型、输出类型和普通算子。普通算子包括卷积、池化、线性激活等算子。

pnnx.Input输入类型算子

对于执行输入类型算子，由于它是输入节点，无需调用 Forward 方法进行算子的计算，只需要将输入节点的输入拷贝到下一级节点即可完成操作。

if (current_op->type == "pnnx.Input"){
    current_op->has_forward = true;
    ProbeNextLayer(current_op, inputs);
}

pnnx.Output输出类型算子

通过设置 current_op->has_forward = true，标记这个输出操作符已经完成前向计算。从 current_op 的 input_operands_seq 中获取输入操作数，并将其设置为 current_op->output_operands。这里假设输出操作符只有一个输入。

else if (current_op->type == "pnnx.Output") {
  current_op->has_forward = true;
  CHECK(current_op->input_operands_seq.size() == 1);
  current_op->output_operands = current_op->input_operands_seq.front();
}

普通类型算子

else {
    InferStatus status = current_op->layer->Forward();
    CHECK(status == InferStatus::kInferSuccess)
        << current_op->layer->layer_name()
        << " layer forward failed, error code: " << int(status);
    current_op->has_forward = true;
    ProbeNextLayer(current_op, current_op->output_operands->datas);
}

// Forward方法完成了计算，并且把输出存放在current_op的输出张量空间中
// ProbeNextLayer要把current_op的输出张量传递到下一级、后继节点的输入空间当中。

执行普通类型的算子和执行输入类型的算子流程大致相同。但是在执行普通类型的算子时，先调用当前算子的Forward重载函数，Forward函数中会根据各类算子自定义的计算逻辑对输入张量完成计算，例如卷积算子就对输入张量计算卷积，池化算子在Forward函数就对输入张量计算池化。在当前算子执行完毕后，通过ProbeNextLayer函数将当前节点的输出赋值给后继节点的输入张量，具体流程同上所述。

在所有算子执行完毕后，需要在所有算子的合集中查询与output_name名称对应的算子（output_op），然后获取该算子对应的输出张量，从执行图中提取最终的输出数据，即整个模型的推理输出output_operand。

// 在build阶段已经指定了output_name_，找到output_name_对应的算子
if (operators_maps_.find(output_name_) != operators_maps_.end()) {
    const auto& output_op = operators_maps_.at(output_name_);
    CHECK(output_op->output_operands != nullptr)
        << "Output from" << output_op->name << " is empty";
    const auto& output_operand = output_op->output_operands;
    // 返回输出算子对应的output张量空间
    return output_operand->datas;
}

首先检查 operators_maps_中是否存在名为 output_name_ 的节点（输出节点）。如果输出操作数有效，代码从输出操作数中提取出数据 (output_operand->datas) 并返回。这个数据就是整个计算图最终的输出结果。最后output_operand会再作为Graph.Forward函数调用输出（模型的预测输出）的返回。