C语言基础（二十六）

news2024/9/22 12:48:52

二叉树节点通常包含三个部分：存储数据的部分、指向左子节点的指针、以及指向右子节点的指针。

测试代码：

#include "date.h" 
#include <stdio.h>  
#include <stdlib.h>  
#include <time.h> 
// 定义二叉树节点的结构，包括节点的值、指向左子节点的指针和指向右子节点的指针。
typedef struct TreeNode {  
    int value;  
    struct TreeNode *left;  
    struct TreeNode *right;  
} TreeNode;  
// 创建一个新的树节点，并分配内存。如果内存分配失败，则打印错误信息并退出程序。 
TreeNode* createNode(int value) {  
    TreeNode* newNode = (TreeNode*)malloc(sizeof(TreeNode));  
    if (newNode == NULL) {  
        printf("Memory allocation failed\n");  
        exit(1);  
    }  
    newNode->value = value;  
    newNode->left = NULL;  
    newNode->right = NULL;  
    return newNode;  
}  
  
// 递归调用：将新值插入到二叉搜索树中的适当位置。
// 如果根节点为空，则新节点成为根节点；
// 如果新值小于根节点的值，则递归地在左子树中插入；
// 如果新值大于或等于根节点的值，则递归地在右子树中插入。
// 插入规则由程序员决定。、 
void insertNode(TreeNode** root, int value) {  
    if (*root == NULL) {  
        *root = createNode(value);  
    } else if (value < (*root)->value) {  
        insertNode(&((*root)->left), value);  
    } else {  
        insertNode(&((*root)->right), value);  
    }  
}  
// 递归调用：打印二叉树的内容，同时根据节点的层级打印相应数量的空格，可视化树的形状。  
void printTree(TreeNode* root, int level) {  
    if (root == NULL) return;  
  
    // 打印空格以显示树的层级  
    for (int i = 0; i < level; i++) {  
        printf("   ");  
    }  
    printf("%d\n", root->value);  
  
    // 递归打印左子树和右子树，层级+1  
    printTree(root->left, level + 1);  
    printTree(root->right, level + 1);  
}  
  
int generateRandomNumber(int min, int max) {   
    return min + rand() % (max - min + 1);  
} 
 
void freeTree(TreeNode* root) {  
    if (root != NULL) {  
        // 递归调用释放左子树  
        freeTree(root->left);  
        // 递归调用释放右子树  
        freeTree(root->right);  
        // 释放当前节点  
        free(root);  
    }  
}  
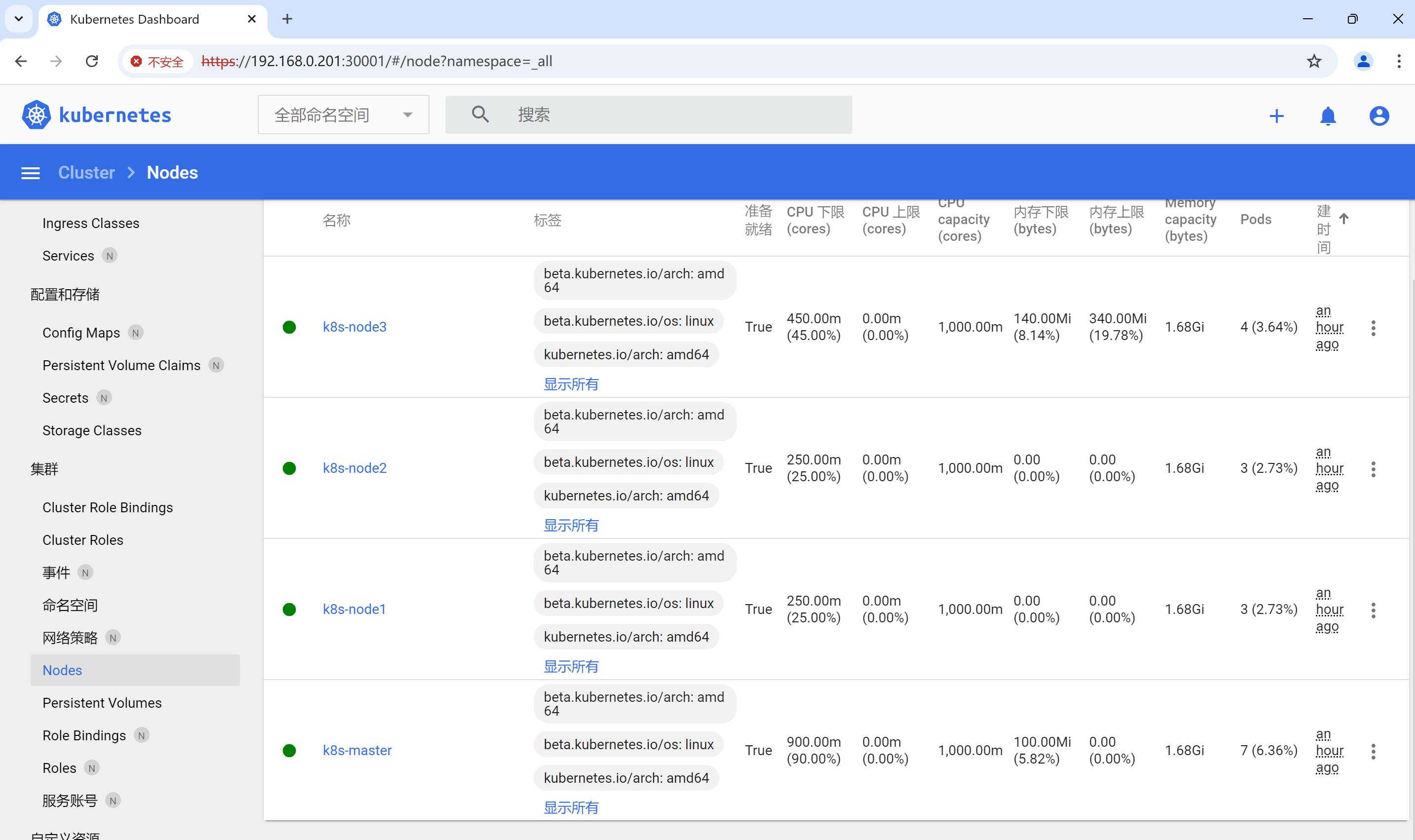
int main() {  

    int times = getTime();
    // 创建一个空的二叉搜索树，并随机插入一系列值。 
    TreeNode* root = NULL; // 初始化为空树  
    srand(time(NULL)); // 设置随机数生成的种子  
    // 插入随机生成的节点  
    for (int i = 0; i < 8; i++) {  
        int randomValue = generateRandomNumber(1, 100); // 生成1到100之间的随机数  
        insertNode(&root, randomValue);  
        printf("Inserted: %d\n", randomValue);  
    }  
  
    // 打印二叉树  
    printTree(root, 0);  
    // 动态释放内存   
    freeTree(root); 
    
    return 0;  
}

运行结果如下：

..........................................................................................................................................................

AVL树是一种自平衡的二叉搜索树，其中每个节点的两个子树的高度最大差别为1，其平衡因子（左子树高度减右子树高度）的绝对值不超过1。在AVL树中进行插入或删除节点后，会破坏树的平衡。为了恢复平衡，需要执行一种或多种旋转操作（单旋转或双旋转）。

测试代码：

#include "date.h"
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
// AVL树 
// 定义结构体 
typedef struct TreeNode {
    int value;
    struct TreeNode *left;
    struct TreeNode *right;
} TreeNode;
// 定义函数createNode，创建新节点并返回指向该节点的指针。
// 如果内存分配失败，则打印错误信息并退出程序。 
TreeNode* createNode(int value) {
    TreeNode* newNode = (TreeNode*)malloc(sizeof(TreeNode));
    if (newNode == NULL) {
        printf("Memory allocation failed:\n");
        exit(1);
    }
    newNode->value = value;
    newNode->left = NULL;
    newNode->right = NULL;
    return newNode;
}
// 定义函数rotateRight，用于向右旋转二叉树节点。
// 将当前节点的左孩子作为新的根节点，调整左右孩子的指向。 
void rotateRight(TreeNode** root) {
    TreeNode* newRoot = (*root)->left;
    (*root)->left = newRoot->right;
    newRoot->right = *root;
    *root = newRoot;
}
// 定义函数rotateLeft，用于向左旋转二叉树节点。
// 将当前节点的右孩子作为新的根节点，调整左右孩子的指向。 
void rotateLeft(TreeNode** root) {
    TreeNode* newRoot = (*root)->right;
    (*root)->right = newRoot->left;
    newRoot->left = *root;
    *root = newRoot;
}
// 定义函数getHeight，用于计算树的高度。
// 递归调用比较左右子树的高度并返回较大值加1: 
int getHeight(TreeNode* root) {  
    if (root == NULL) return 0;  
    return 1 + (getHeight(root->left) > getHeight(root->right) ? getHeight(root->left) : getHeight(root->right));  
} 
// 定义函数rebalance，用于平衡二叉树。
// 通过比较左右子树的高度差来判断是否需要旋转，然后执行相应的旋转操作。 
void rebalance(TreeNode** root) {
    if (*root == NULL) {
        return;
    }
    int leftHeight = getHeight((*root)->left);
    int rightHeight = getHeight((*root)->right);

    if (leftHeight - rightHeight > 1) {
        if (getHeight((*root)->left->left) < getHeight((*root)->left->right)) {
            rotateLeft(&((*root)->left));
        }
        rotateRight(root);
    } else if (rightHeight - leftHeight > 1) {
        if (getHeight((*root)->right->right) < getHeight((*root)->right->left)) {
            rotateRight(&((*root)->right));
        }
        rotateLeft(root);
    }
}
// 定义函数insertNode，用于向树中插入新节点。
// 根据值的大小递归调用，在左右子树中插入节点，并在插入后执行平衡操作。 
void insertNode(TreeNode** root, int value) {
    if (*root == NULL) {
        *root = createNode(value);
    } else if (value < (*root)->value) {
        insertNode(&((*root)->left), value);
    } else {
        insertNode(&((*root)->right), value);
    }
    rebalance(root);
}
// 定义函数printTree，用于按层次打印树。
// 递归调用打印节点值，并通过增加缩进表示树的层次结构。 
void printTree(TreeNode* root, int level) {
    if (root == NULL) return;

    for (int i = 0; i < level; i++) {
        printf("   ");
    }
    printf("%d\n", root->value);

    printTree(root->left, level + 1);
    printTree(root->right, level + 1);
}
// 定义函数generateRandomNumber，用于生成介于[min, max]范围内的随机数。 
int generateRandomNumber(int min, int max) { 
    return min + rand() % (max - min + 1);
}
// 定义函数freeTree，用于释放树的内存。
// 递归调用释放左右子树的内存，并释放根节点的内存。 
void freeTree(TreeNode* root) {
    if (root != NULL) {
        freeTree(root->left);
        freeTree(root->right);
        free(root);
    }
}
// 初始化根节点为NULL，然后随机数生成15个介于1和100之间的值，并插入到树中。
// 插入后打印树结构，并最后释放树的内存。 
int main() {
    int times = getTime();

    TreeNode* root = NULL;
    srand(time(NULL));

    for (int i = 0; i < 15; i++) {
        int randomValue = generateRandomNumber(1, 100);
        insertNode(&root, randomValue);
        printf("Inserted: %d\n", randomValue);
    }
    printTree(root, 0);
    freeTree(root);
   }

运行结果如下：