一、介绍

1.1 概述

R强化学习是机器学习中的一个领域，它引入了智能体在复杂环境中学习最佳策略的概念。代理从其操作中学习，从而根据环境的状态获得奖励。强化学习是一个具有挑战性的话题，与机器学习的其他领域有很大不同。

强化学习的显着之处在于，可以使用相同的算法来使代理适应完全不同的、未知的和复杂的条件。

笔记。为了完全理解本文中包含的概念，强烈建议熟悉前面文章中介绍的蒙特卡洛方法和时间差异学习的基础知识。

1.2 关于此文章

在上一部分中，我们通过结合动态规划原理和 MC 方法分析了 TD 算法的工作原理。此外，我们还研究了一步式 TD 算法 — 最简单的 TD 实现。在本文中，我们将概括 TD 概念，并了解何时使用其他算法变体可能是有利的。

本文基于 Richard S. Sutton 和 Andrew G. Barto 撰写的《强化学习》一书的第 7 章。我非常感谢为本书的出版做出贡献的作者们的努力。

二、想法

        让我们暂停一下，了解一下一步式 TD 和 MC 算法有什么共同点。如果我们省略过于具体的细节，我们会注意到它们实际上非常相似，并且使用相同的状态更新规则，除了一个区别：

• 一步 TD 通过查看 n = 1 下一个状态来更新每个状态。
• MC 在分析了整个剧集后更新了每个状态。这可以粗略地看作是 n 步后发生的每个状态的更新（其中 n 可能是一个很大的数字）。

        我们有两个极端情况，其中 n = 1，其中 n = 剧集序列中剩余状态的数量。一个合乎逻辑的问题出现了：我们是否可以使用位于这些极端值中间某个位置的 n 值？

        答案是肯定的。这个概念通过 n 步 Bootstrapping 进行了推广。

n 步 Bootstrapping 泛化了 TD 算法

2.1 工作流

        在一步 TD 中，我们分析收到的奖励与状态值如何变化之间的差异，从当前状态切换到下一个状态 （n = 1）。这个想法可以很容易地推广到多个步骤。为此，我们引入 n 步返回，它计算当前状态 t 和未来状态在步骤 t + n 之间的累积折扣奖励。此外，它还在步骤 t + n 处添加状态值。

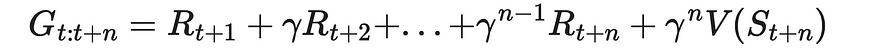
        n 步返回

        使用之前文章中介绍的类似更新规则，这次我们可以将 n 步返回值与当前状态值进行比较，并得出新的更新规则：

        更新 n 步引导的规则

        为了更好地理解工作流程，让我们绘制一个 n 的几个值的状态关系图。下图演示了如何使用有关下一个状态和奖励的信息来更新序列中的先前状态。

        不同 n 值更新期间奖励和状态值之间的关系

例如，让我们以 3 步 TD 为例：

• 剧集的开头一直生成到状态 S₃。
• 状态 S₀ 使用 3 步返回进行更新，该回报将奖励 R₁、R₂ 和 R₃ 以及状态 S₃ 的值相加。
• 生成状态 S₄。
• 状态 S₁ 使用 3 步返回进行更新，该回报将奖励 R₂、R₃ 和 R₄ 以及状态 S₄ 的值相加。
• 生成状态 S₅。
• 状态 S₅ 使用 3 步返回进行更新，该回报将奖励 R₃、R₄ 和 R₅ 以及状态 S₅ 的值相加。
• 重复类似的过程，直到我们到达情节的最后一个状态。

如果对于给定状态，用于计算 n 步返回的剩余状态少于 n 个，则使用截断的 n 步返回，累积可用奖励，直到最终状态。

如果 n = ∞，则 n 步 TD 是蒙特卡洛算法。

2.2 n 级 TD 控制

        在第 5 部分中，我们讨论了 Sarsa、Q-learning 和预期 Sarsa 算法。所有这些都是基于使用下一个州的信息。正如我们在本文中所做的，我们可以将这个想法扩展到 n 步学习。为此，唯一需要做的更改是调整他们的更新公式，以使用不是来自下一个状态的信息，而是来自 n 步之后的信息。其他一切都将保持不变。

三、选择 n 的最佳值

        在第 5 部分中，我们还强调了一步式 TD 算法相对于 MC 方法的优势，以及它们如何实现更快的收敛。如果是这样，为什么不总是使用 one-step TD 而不是 n 步法呢？在实践中，n = 1 并不总是最佳值。让我们看一下 Richard S. Sutton 和 Andrew G. Barto 的 RL 书中提供的一个例子。此示例显示了使用较大的 n 值可优化学习过程的情况。

        下图显示了代理在 Sarsa 算法的第一集期间在给定迷宫中绘制的路径。代理的目标是找到到 X 的最短路径。当代理踩到 X 时，它会收到奖励 R = 1。在迷宫中每走一步，奖励 R = 0。

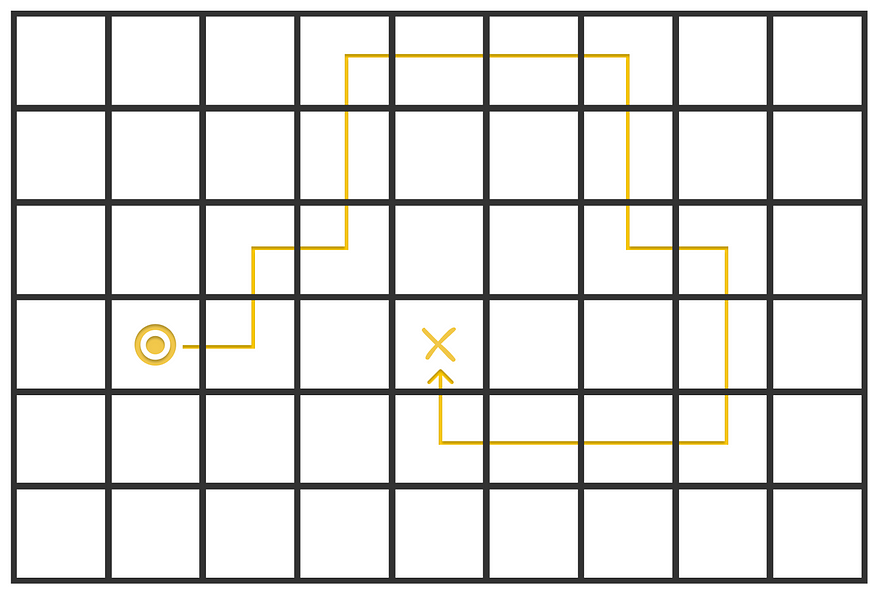
        代理在迷宫中绘制的路径。X 标记表示终端状态。图片由作者改编。来源：强化学习。引言。第二版 |Richard S. Sutton 和 Andrew G. Barto

现在让我们比较一下代理在 1 步 Sarsa 和 10 步 Sarsa 中的学习方式。我们假设所有操作值都初始化为 0。

在 1 步式 Sarsa 中，对于每个移动，仅根据下一个状态的信息执行更新。这意味着，唯一具有有意义更新的 action 值是在单个步骤中直接指向目标 X 的操作值。在这种情况下，代理获得正奖励，从而了解到做出 “up” 最后一步确实是一个最佳决定。但是，所有其他更新不会产生任何影响，因为收到的奖励 R = 0 不会更改任何操作值。

另一方面，在 10 步 Sarsa 中，最终步会将其正奖励传播到最后 10 步的行动值。通过这种方式，代理将从剧集中学到更多信息。

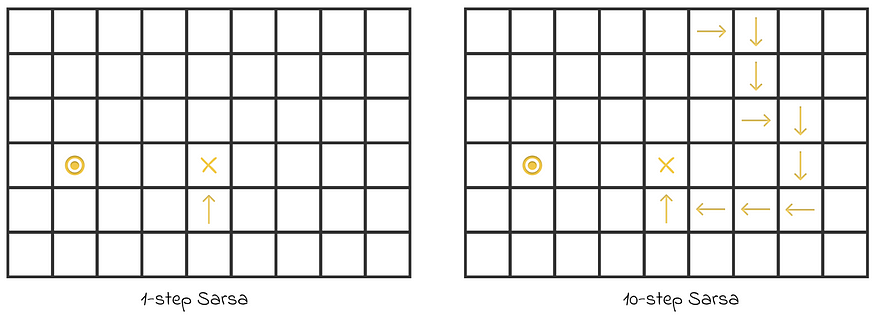
在第一集中，其值在两种算法中都被修改的动作状态的可视化。正如我们所看到的，10 步 Sarsa 的学习速度比 1 步 Sarsa 快得多。图片由作者改编。来源：强化学习。引言。第二版 |Richard S. Sutton 和 Andrew G. Barto

因此，在这些迷宫设置中，较大的 n 值会使代理学习得更快。

看了这个例子，我们可以得出一个重要的事实：

n 在时间差异学习中的最佳值是与问题相关的。

四、结论

将一步 TD 和蒙特卡洛方法推广到 n 步算法中，在强化学习中起着重要作用，因为 n 的最佳值通常位于这两个极端之间。

除此之外，没有选择最佳 n 值的一般规则，因为每个问题都是唯一的。虽然 n 值较大会导致更新延迟更多，但它们仍然比较小的值表现得更好。理想情况下，应该将 n 视为超参数并仔细选择它以找到最优值。

资源

• 强化学习。引言。第二版 |Richard S. Sutton 和 Andrew G. Barto

除非另有说明，否则所有图片均由作者提供。