author: xiao黄
time: 2024-08-28
公众号: 复杂网络与网络科学
CSDN: https://blog.csdn.net/Python_Matlab

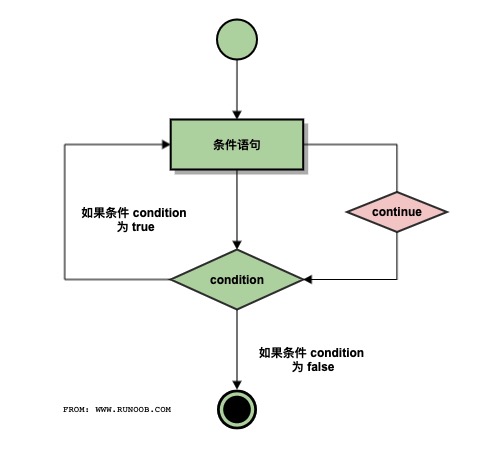
评价节点重要性算法的指标有多种，如基于信息传播方面的动力学模型、单调性、Distinct Metric以及基于网络脆弱性和鲁棒性的方法等。不同的评价指标所考虑的角度不同，基于信息传播方面的动力学模型是通过衡量节点的传播范围以此来判定节点的重要程度，通常所使用的信息传播方面的动力学模型有 SI 和 SIR 等；单调性和Distinct Metri是检验节点重要性算法区分节点的能力，节点重要性越能区分不同节点的重要性，单调性值越趋近于 1，当每个节点都有一个不同的重要性值时，单调性值为 1；而基于网络的脆弱性和鲁棒性的方法则是通过移除网络中的节点后，通过最大连通子图系数和网络效率等指标的变化反映出网络中的节点被移除后对网络造成影响，进而衡量节点重要性算法的优劣，以此衡量节点的重要性，其中移除节点有两种方式，其一是随机移除，其二是根据节点重要性算法得到的结果按从大到小的序列进行移除。其流程如图所示。

（1）最大连通子图
对于复杂网络来说，任何一个节点的行为都有可能影响整体网络的连通性，而最大连通子图系数是用来评估网络连通性的指标。将网络中的所有节点按重要性排序算法进行排序，移除节点后，对网络连通性的影响。最大连通子图系数(LCC)的计算公式如下：

式中，N’表示移除节点后的网络中的最大连通子图系数的节点数目，N表示网络的节点数量。若最大连通子图系数随着节点移除而变小的趋势越明显，说明节点重要性排序算法越准确。
（2）网络效率
利用网络中节点间信息交换的效率来评价节点重要性排序算法。使用网络效率来量化网络中交换信息的效率，用于评价网络连通性的强弱。计算公式如下：