客户特征分析

识别不同类型的客户群体，以便更好地理解客户行为、优化营销策略并提高客户满意度

1. 数据集

数据集见 数分基础（01）示例数据集Global_Superstore

2. 思路与步骤

2.1 特征工程

客户群体特征，可以从购买行为、地理位置等多个维度进行区分。

• 客户行为特征，例如购买频率、平均订单金额、总购买金额、退货次数等；
• 地理位置特征，通常包括国家、省市等信息；
• 时间特征，通常有季节、月份、工作日/周末等；
• 其他特征，例如年龄、性别等。

2.2 识别方法

通常使用聚类算法对客户进行细分。常用的有：K-Means聚类、层次聚类、RFM分析等

2.3 可视化

散点图、热图等方式来展示不同群体特征，帮助业务理解客户群体有哪些

3. 分析准备

读取数据集并进行基本的数据预处理

3.1 读取数据集

先看看Excel文档有哪些 sheet

import pandas as pd

# Load the dataset from the provided Excel file
file_path = "Global_Superstore2.xlsx"

# Read the first sheet to understand the data structure
xls = pd.ExcelFile(file_path)
sheet_names = xls.sheet_names
sheet_names

运行结果

只有一个sheet，那么再看看这个表格有哪些字段，数据记录大体是怎样的

# Load the data from the identified sheet
data = pd.read_excel(file_path, sheet_name='Sheet1')

# Display the first few rows and basic information about the dataset
data.head(), data.info()

运行结果为：


数据集包含了51290条记录和24个字段，可以逐一过一下字段名称，搭配前5行记录数据，从中找到和这次分析相关的关键数据列：

• 客户信息：Customer ID、Customer Name、Segment
• 地理位置：City、State、Country、Region
• 购买行为：Sales、Quantity、Profit、Discount

3.2 识别不同客户群体

3.2.1 使用K-Means聚类进行初步细分

• 聚类前对数值型数据进行标准化（例如使用Min-Max Scaling）
• 选取与客户行为相关的特征，如购买频率、平均订单金额等
• 使用肘部法、轮廓系数或平均轮廓距离等方法来确定最优的聚类数量
• 对标准化后的数据进行K-Means聚类

代码

from sklearn.preprocessing import StandardScaler
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
from matplotlib import font_manager


# 步骤1: 客户特征
# 根据客户ID进行分组，获取客户特定的度量指标
customer_data = data.groupby('Customer ID').agg({
    'Sales': 'sum',      # 总销售额
    'Quantity': 'sum',   # 总购买数量
    'Profit': 'sum',     # 总利润
    'Discount': 'mean'   # 平均折扣
}).reset_index()

# 重命名列名以便更清晰
customer_data.columns = ['Customer ID', 'Total Sales', 'Total Quantity', 'Total Profit', 'Average Discount']

# 步骤2: 特征缩放
scaler = StandardScaler()
scaled_features = scaler.fit_transform(customer_data[['Total Sales', 'Total Quantity', 'Total Profit', 'Average Discount']])

# 步骤3: 使用肘部法确定最佳聚类数
# 调整范围以加速计算并找到最佳聚类数
inertia_optimized = []
for n in range(1, 6):  # 将范围缩小到较少的聚类数
    kmeans = KMeans(n_clusters=n, random_state=42)
    kmeans.fit(scaled_features)
    inertia_optimized.append(kmeans.inertia_)


# 设置中文字体为 SimHei（黑体）
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

# 绘制优化的肘部图
plt.figure(figsize=(8, 5))
plt.plot(range(1, 6), inertia_optimized, marker='o')
plt.xlabel('聚类数量')
plt.ylabel('惯性')
plt.title('肘部法 (优化) 以确定最佳聚类数量')
plt.grid(True)
plt.show()

3.2.2 关于聚类方法

（1）特征缩放

是对数据进行预处理的重要步骤，将数据中的不同特征调整大同一量纲，方法常用标准化和归一化。这么做的主要目的是使得所有特征对模型的影响力相似。

1）平衡特征对模型的影响力，避免某些特征因为数值范围较大而主导聚类结果

不同特征的数值范围可能相差较大，例如，销售额可能是几千到几万，而折扣率通常在 0 到 1 之间。直接使用这些未经处理的数据会导致高数值范围的特征主导聚类结果

2）提高算法效率

K-Means依赖于距离计算，特征缩放能够让距离计算更加准确和稳定

在代码中使用了标准化方法

# 步骤2: 特征缩放
scaler = StandardScaler()
scaled_features = scaler.fit_transform(customer_data[['Total Sales', 'Total Quantity', 'Total Profit', 'Average Discount']])

利用 StandardScaler()对数据进行缩放处理，fit_transform 方法将选定的特征（总销售额、总购买数量、总利润、平均折扣）进行标准化，标准化后的数据将被输入聚类算法，使得每个特征在同等条件下对结果产生影响。具体：首先，对于每个特征，计算其平均值和标准差；其次，进行数据转换，将每个特征值减去该特征的均值，再除以该特征的标准差，使得转换后的数据具有零均值和单位方差。

（2）使用肘部法ElbowMethod确定最佳聚类数

选择适当的聚类数（簇的数量），肘部法是一个常用的启发式方法，用于确定这个合适的数量。

肘部法，绘制不同聚类数下的模型误差或惯性来评估聚类效果

惯性是指每个样本到其最近聚类中心的距离平方和的总和，是衡量聚类紧密度的指标，惯性越小，说明样本距离各自簇中心越近，聚类效果越好。

# 步骤3: 使用肘部法确定最佳聚类数
# 调整范围以加速计算并找到最佳聚类数
inertia_optimized = []
for n in range(1, 6):  # 将范围缩小到较少的聚类数
    kmeans = KMeans(n_clusters=n, random_state=42)
    kmeans.fit(scaled_features)
    inertia_optimized.append(kmeans.inertia_)

1）计算不同聚类数下的惯性

从聚类数为1开始，逐步增加聚类数，计算每个聚类数下的惯性值

• for n in range(1, 6)，测试从1到5的聚类数量。当然也可以是从 1 到 10 或更大，但计算时间会很长，所以选择 1 到 5 的范围，如果从结果看出合适的聚类数在这个范围内，可以进一步缩小，如果不在，可以进一步扩大范围

• kmeans = KMeans(n_clusters=n, random_state=42)。创建一个 K-Means 聚类模型，n_clusters=n 指定当前循环的聚类数，random_state=42 是在使用 K-Means 聚类（或其他随机算法）时，为确保结果可重复的一种设置方式。
  – random_state：K-Means 算法，初始随机选择聚类中心点（质心），因此，每次运行算法时，即使输入的数据相同，输出的结果也可能不同。通过设置 random_state，可以固定随机种子，使得每次运行算法时的随机数序列相同
  例如，

# 不同的 random_state 会导致不同的初始化，结果也可能不同
kmeans_1 = KMeans(n_clusters=3, random_state=42)
kmeans_2 = KMeans(n_clusters=3, random_state=1)

# 如果 random_state 设置相同，结果将一致
kmeans_3 = KMeans(n_clusters=3, random_state=42)

kmeans_1 和 kmeans_3 会产生相同的聚类结果，kmeans_2 的结果可能不同

– 42 只是一个习惯用法，可选任何整数值，只要保证每次运行时使用相同的值即可。“42”只是常被编程和数据科学用于默认示例的数字（具体可以搜关键词“《银河系漫游指南》中“生命、宇宙及一切的答案 数字42”）

– 在 KMeans(n_clusters=n, random_state=42) 中，每次运行 K-Means 聚类时，算法都会以相同的方式初始化聚类中心，确保同样的数据产生相同的结果

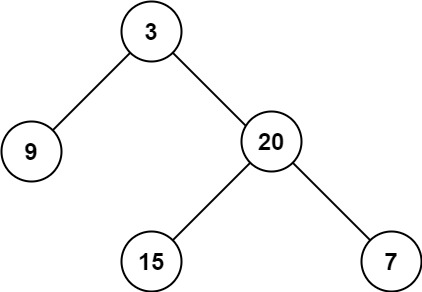
2）绘制惯性曲线，寻找肘部点，即寻找合适的聚类数

不同聚类数对应的惯性值，绘制成曲线，观察，当增加聚类数时，惯性下降速度明显减缓，形成类似“肘部”的位置，这个点即为推荐的最合适的聚类数

• X轴 —— 聚类数量
• Y轴 —— 惯性值，衡量聚类内部的紧密度，越小，样本点越靠近各自的中心，好
• 趋势，聚类数增加，惯性值逐渐下降，因为增加聚类数会使每个簇中的点更靠近其中心点
• 下降速度，最初从一个簇到2个簇、再到3个簇，惯性值下降较快；
• 寻找，当聚类数量从2增加到3时，惯性下降的速度，比，从3到4惯性下降的速度快，类似“肘部”的转折点 —— 3
• 解释，惯性显著降低直到3个簇，意味着聚类质量提升明显，但是超过3个簇，惯性值下降速度变缓，意味着增加聚类数量改进不大，反而增加了复杂性

意义，肘部分析帮助我们合理选择聚类数量，使得模型既能够合理划分客户群体，又不会因为过多的聚类簇而导致结果过于复杂。

接下来，选择3个聚类数目进行客户群体细分。

4.客户群体分析

4.1 划分类别

按照前面讨论的，指定聚类数量为 3 ，将客户数据分为 3 个类，用 K-Means算法进行分类

# 设置 Pandas 显示浮点数格式，禁用科学计数法
pd.set_option('display.float_format', '{:.2f}'.format)

# 使用确定的聚类数量进行 K-Means 聚类
optimal_clusters = 3
kmeans_model = KMeans(n_clusters=optimal_clusters, random_state=42)
customer_data['Cluster'] = kmeans_model.fit_predict(scaled_features)

4.2 汇总各类特征

汇总每类客户特征，了解每类客户的销售额、购买数量、利润的均值和总和，了解每类客户的平均折扣，了解每类客户的数量

cluster_summary = customer_data.groupby('Cluster').agg({
    'Total Sales': ['mean', 'sum'],         # 总销售额的均值和总和
    'Total Quantity': ['mean', 'sum'],      # 总购买数量的均值和总和
    'Total Profit': ['mean', 'sum'],        # 总利润的均值和总和
    'Average Discount': 'mean',             # 平均折扣
    'Customer ID': 'count'                  # 每个聚类中的客户数量
}).reset_index()

重命名列名，便于理解和查看

cluster_summary.columns = [
    'Cluster', 'Avg Total Sales', 'Sum Total Sales', 
    'Avg Total Quantity', 'Sum Total Quantity', 
    'Avg Total Profit', 'Sum Total Profit', 
    'Avg Discount', 'Customer Count'
]
print(cluster_summary)

4.3 “4.1-4.2”完整代码及运行结果

# 设置 Pandas 显示浮点数格式，禁用科学计数法
pd.set_option('display.float_format', '{:.2f}'.format)

# 使用确定的最佳聚类数量进行 K-Means 聚类（这里为了简化选择 3 个聚类数）
optimal_clusters = 3
kmeans_model = KMeans(n_clusters=optimal_clusters, random_state=42)
customer_data['Cluster'] = kmeans_model.fit_predict(scaled_features)

# 汇总各个聚类的特征以了解其特性
cluster_summary = customer_data.groupby('Cluster').agg({
    'Total Sales': ['mean', 'sum'],         # 总销售额的均值和总和
    'Total Quantity': ['mean', 'sum'],      # 总购买数量的均值和总和
    'Total Profit': ['mean', 'sum'],        # 总利润的均值和总和
    'Average Discount': 'mean',             # 平均折扣
    'Customer ID': 'count'                  # 每个聚类中的客户数量
}).reset_index()

# 重命名列名以便更清晰
cluster_summary.columns = [
    'Cluster', 'Avg Total Sales', 'Sum Total Sales', 
    'Avg Total Quantity', 'Sum Total Quantity', 
    'Avg Total Profit', 'Sum Total Profit', 
    'Avg Discount', 'Customer Count'
]

# 打印聚类汇总表
print(cluster_summary)

# 还原 Pandas 默认显示设置（可选）
pd.reset_option('display.float_format')

4.4 结果分析

数据被分为三个聚类，即具有不同特征的客户群体，逐一看过来

Cluster 0 - 2

Cluster 0
平均总销售额 2841.24
总销售额	1,693,380.35
平均总购买数量 39.92
总购买数量	2,3792
平均利润	395.61
总利润	235,785.89
平均折扣	0.09
客户数量	596

Cluster 1
平均总销售额 14464.10
总销售额	10,399,685.24
平均总购买数量	202.25
总购买数量	145,416
平均利润	1,843.55
总利润	1,325,512.06
平均折扣	0.13
客户数量	719

Cluster 2
平均总销售额 1997.95
总销售额	5,49,436.32
平均总购买数量	33.11
总购买数量	9104
平均利润	-341.24
总利润	-93840.66
平均折扣	0.34
客户数量	275

5. 你看出来了什么？

简要总结如下：
Cluster 0 平均购买量和销售额相对适中，利润正，折扣较低
Cluster 1 销售额和购买量均为最高，带来利润最高，虽然折扣比 Cluster 0高，但是高购买量和高单笔交易值，成为公司最重要的利润来源
Cluster 2 平均购买金额和数量最低，利润为负，高折扣和低利润，带来小收益甚至损失

很明显，Cluster 2 客户是聪明的“薅羊毛”高手~~~能够利用折扣和优惠来最大化自己的购买价值，通过理性和策略性的购买来减少生活开支，价格敏感、不迷信某种品牌（品牌忠诚度低），这不仅是一种购物习惯，某种意义上也是一种理财方式。

然而，站在公司立场，Cluster 2 客户享受了高折扣，却带来了负利润，确实是需要优化的对象，但优化的同时也要保持一定的吸引力，避免过于苛刻的策略导致这部分客户中的潜在客户流失。

这部分群体既是挑战也是机会，需要通过更合理的策略，例如，设置最低消费门槛、调整折扣策略、会员积分优惠等等，将他们从“薅羊毛”型转化为更有价值的长期客户。

6. 简单可视化