目录
一、介绍
1.1 强化学习
2.1 关于此文章
三、ε贪婪策略
四、蒙特卡洛控制
4.1 基本原理
4.2 举个例子
五、On-policy & off-policy 方法
六、重要性采样
6.1 赋予动机
6.2 想法
6.3 应用
七、增量实施
7.1 增量的理论
7.2 常α MC
八、结论
一、介绍
1.1 强化学习
R强化学习是机器学习中的一个领域,它引入了代理的概念,代理必须在复杂环境中学习最佳策略。代理从其操作中学习,这些操作会在给定环境状态的情况下产生奖励。强化学习是一个困难的话题,与机器学习的其他领域有很大不同。这就是为什么它应该只在给定的问题无法通过其他方式解决时使用。
强化学习的不可思议之处在于,可以使用相同的算法来使代理适应完全不同的、未知的和复杂的条件。
特别是,Monte Carlo 算法不需要任何有关环境动态的知识。这是一个非常有用的属性,因为在现实生活中我们通常无法访问此类信息。在上一篇文章中讨论了蒙特卡洛方法背后的基本思想之后,这次我们将重点介绍改进它们的特殊方法。
笔记。要完全理解本文中包含的概念,强烈建议熟悉本系列文章第 3 部分中介绍的蒙特卡洛算法的主要概念。
2.1 关于此文章
本文是上一部分的逻辑延续,在上一部分,我们介绍了使用 Monte Calro 方法估计价值函数的主要思想。除此之外,我们还讨论了强化学习中著名的探索与利用问题,以及如果我们只使用贪婪策略,它如何阻止代理进行有效学习。
我们还看到了 exploring starts 方法,可以部分地解决这个问题。另一个很棒的技术包括使用 ε贪婪策略,我们将在本文中介绍。最后,我们将开发另外两种技术来改进 Naive GPI 实现。
本文部分基于 Richard S. Sutton 和 Andrew G. Barto 撰写的《强化学习》一书的 C章节 2 和 5。我非常感谢为本书的出版做出贡献的作者们的努力。
笔记。本文的源代码可在 GitHub 上找到。顺便说一句,该代码会生成未在 GitHub 笔记本中呈现的 Plotly 图。如果要查看图表,可以在本地运行 notebook 或导航到存储库的 results 文件夹
二、ε贪婪策略
如果所有 s ∈ S > 0 且 a ∈ A 的 π(a | s) 为 0,则该策略称为软策略。 换句话说,从给定状态 s 中选择任何操作的概率总是非零。
如果 ε π(a | s) ≥ ε / |A(s)|对于所有 s ∈ S 和 a ∈ A。
在实践中,ε 软策略通常接近于确定性(ε 是一个较小的正数)。也就是说,有一个动作要以非常高的概率选择,其余的概率在其他动作之间分配,每个动作都有一个保证的最小概率 p ≥ ε / |A(s)|.
如果策略的概率为 1-ε,它选择具有最大回报的操作,并且概率为 ε,则称为 ε-greedy,它随机选择一个操作。
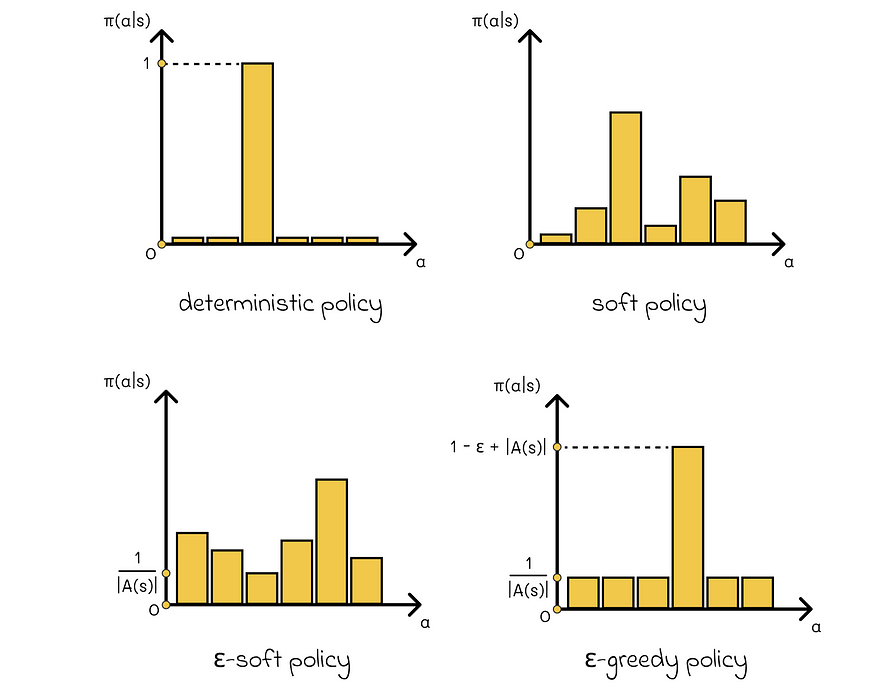
不同类型的策略
根据 ε 贪婪策略的定义,任何行动都可以等概率 p = ε / |A(s)|.其余的概率,即 1 — ε,被添加到具有最大回报的动作中,因此它的总概率等于 p = 1 — ε + ε / |A(s)|.
关于ε贪婪策略的好消息是它们可以集成到策略改进算法中!根据该理论,GPI 并不要求更新后的策略对值函数严格贪婪。相反,它可以简单地转向贪婪策略。特别是,如果当前策略是 ε 软策略,则保证任何针对 V 或 Q 函数更新的ε贪婪策略都优于或等于 π。
三、蒙特卡洛控制
3.1 基本原理
在 MC 方法中寻找最优策略的方式与我们在上一篇文章中讨论的基于模型的算法的方式相同。我们从初始化任意策略π开始,然后策略评估和策略改进步骤相互交替。
术语 “控制” 是指寻找最佳策略的过程。

MC 方法中政策评估 (E) 和政策改进 (I) 之间的迭代交替。图片由作者改编。来源:强化学习。引言。第二版 |Richard S. Sutton 和 Andrew G. Barto
- Q-function 是通过对许多情节进行采样并平均返回值来计算的。
- 策略改进是通过使策略相对于当前值函数贪婪(或ε贪婪)来完成的。
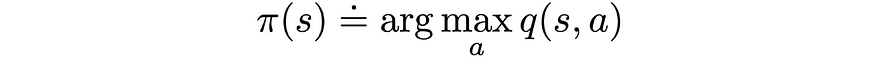
贪婪策略更新。来源:强化学习。引言。第二版 |Richard S. Sutton 和 Andrew G. Barto
理论上,我们必须运行无限数量的集才能获得 Q 函数的精确估计。在实践中,它不是必需的,我们甚至可以为每个策略改进步骤只运行一次策略评估迭代。
另一个可能的选项是仅使用单个剧集来更新 Q-function 和策略。在每个剧集结束后,计算的返回值将用于评估策略,并且仅针对剧集期间访问的州更新策略。

用于 Q 函数估计的 Monte Carlo 算法与探索开始策略。来源:强化学习。引言。第二版 |Richard S. Sutton 和 Andrew G. Barto
在提供的 exploring starts 算法版本中,考虑了每对 (state, action) 的所有返回,尽管使用不同的策略来获取它们。
使用 ε-greedy 策略的算法版本与前一个完全相同,除了以下小变化:
- π 被初始化为任意 ε-soft 策略;
- 包括起始对 (S₀, A₀) 在内的整个轨迹是根据策略 π 选择的;
- 在更新期间,策略π始终保持ε贪婪状态:
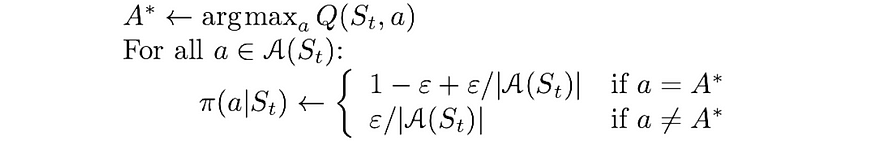
用于 Q 函数估计的 Monte Carlo 算法的 ε-greedy 策略更新规则。来源:强化学习。引言。第二版 |Richard S. Sutton 和 Andrew G. Barto
3.2 举个例子
通过了解 Monte Carlo 控制的工作原理,我们现在都可以找到最佳策略。让我们回到上一篇文章中的二十一点例子,但这次我们将研究一个最佳策略及其相应的 Q-function。基于这个例子,我们将做出一些有用的观察。
Q 函数
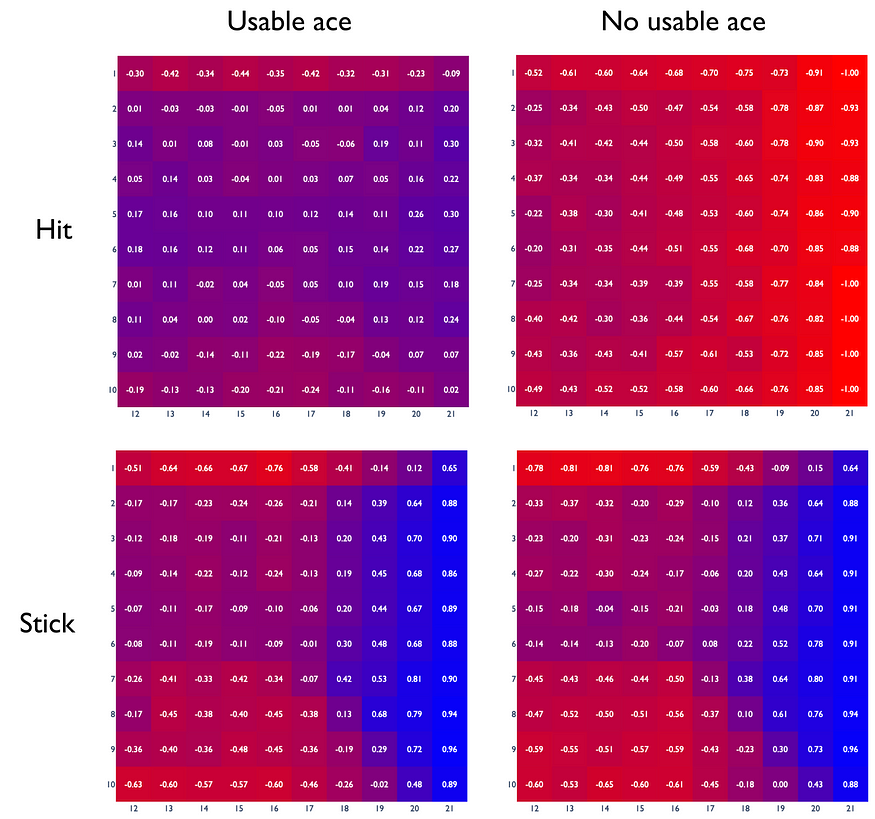
最佳策略的 Q 函数 (ε = 0.1, α = 0.005)。α 是指常数 α MC 实现中的学习率(在上一节中解释)。
构造的图显示了最优策略下的 Q-函数示例。实际上,它可能与真实的 Q-function 有很大不同。
让我们取 q 值等于 -0.88,当庄家有 6 点时,玩家决定在没有可用 A 的情况下拿到 21 点。很明显,在这种情况下,玩家总是会输。那么为什么在这种情况下 q 值不等于 -1呢?以下是主要的两个原因:
- 在训练开始时,该算法不太清楚哪些操作更适合某些状态,并且几乎随机地选择它们。事实证明,在某些时候,两个操作之间的 q 值差异会变得相当大。因此,在策略改进步骤中,算法总是会贪婪地选择奖励最大的动作。因此,其他回报率较低的操作将永远不会再次采样,并且其真实 q 值将无法得到充分计算。如果我们查看相同的状态,唯一的差异是庄家有 7 个点,那么 q 值等于 -1,这实际上是真的。因此,正如我们所看到的,由于其随机性质,该算法对于相似状态的收敛方式不同。
- 我们将α设置为 0.005(在下面的“常数 α MC”部分中解释),这意味着算法需要一些时间才能收敛到正确的答案。如果我们使用超过 5 ⋅ 10⁶ 次迭代或使用其他值进行α,则估计值可能会更接近 -1。
最优策略
要从构建的 Q-Function 中直接获得最优策略,我们只需要比较相同状态下的 hit 和 stick 动作的回报,并选择 q 值更大的动作。
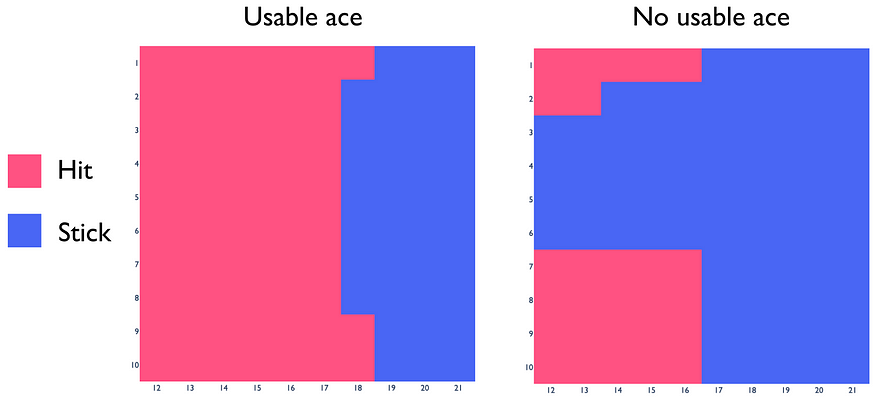
从构建的 Q-function 衍生出的最优 Blackjack 策略。
事实证明, 得到的 blackjack 策略非常接近真正的最优策略。这一事实表明我们为 ε 和 α 选择了良好的超参数值。对于每个问题,它们的最佳值都不同,应适当选择。
四、On-policy & off-policy 方法
考虑一个强化学习算法,该算法生成代理的轨迹样本,以估计其在给定策略下的 Q 函数。由于某些状态非常罕见,因此该算法显式对它们进行采样的频率高于它们自然出现的频率(例如,explosing starts)。这种方法有什么问题吗?
事实上,样本的获取方式将影响价值函数的估计,因此也会影响策略。结果,我们获得了在采样数据代表真实状态分布的假设下完美工作的最佳策略。但是,这个假设是错误的:实际数据具有不同的分布。
不考虑此方面使用不同采样数据查找策略的方法称为 on-policy 方法。我们之前看到的 MC 实现是 on-policy 方法的一个示例。
另一方面,有一些算法会考虑数据分布问题。一种可能的解决方案是使用两个策略:
- 行为策略用于生成采样数据。
- 学习 Target 策略并用于查找代理的最佳策略。
同时使用 behaviour 和 target 策略的算法称为 off-policy methods。在实践中,与政策方法相比,它们更复杂,更难收敛,但与此同时,它们会带来更精确的解决方案。
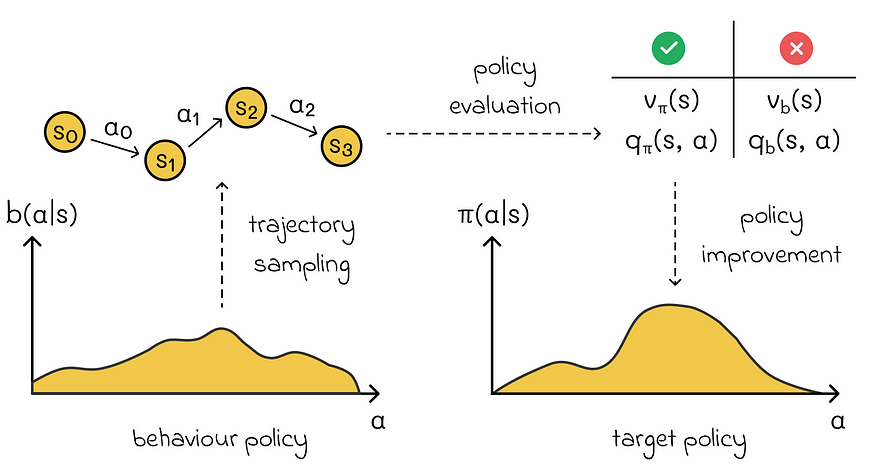
非策略方法使用 behaviour 策略对数据进行采样,但需要进行调整,以便可以适当地学习目标策略。实现它的方法之一是通过 behaviour 策略下的 value functious 获取 target 策略下的值函数(该算法将在下面的部分中讨论)。
为了能够估计策略 b 到 π,必须保证覆盖率标准。它指出 π(a | s) > 0 意味着所有 a ∈ A 和 s ∈ S 的 b(a | s) > 0。换句话说,对于策略 π 下的每个可能操作,在策略 b 中观察到该操作的概率必须不为零。否则,就无法估计该操作。
现在的问题是,如果我们使用另一个行为策略对数据进行采样,我们如何估计目标策略?这就是重要性抽样发挥作用的地方,它几乎用于所有非策略方法。
五、重要性采样
在机器学习算法中,计算预期值很常见。但是,有时它可能很困难,需要使用特殊技术。
5.1 赋予动机
让我们想象一下,我们在 f(x) 上有一个数据分布(其中 x 是一个多维向量)。我们将用 p(x) 表示它的概率密度函数。
我们想找到它的期望值。根据整型定义,我们可以写成:
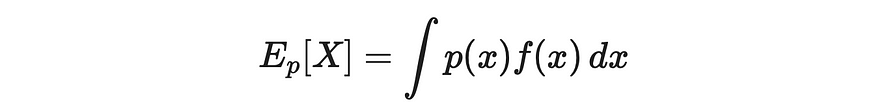
通过积分定义期望值
假设由于某些原因,计算这个表达式是有问题的。事实上,计算精确的整数值可能很复杂,尤其是当 x 包含大量维度时。在某些情况下,从 p 分布中采样甚至是不可能的。
正如我们已经了解到的,MC 方法允许通过平均值来近似预期值:
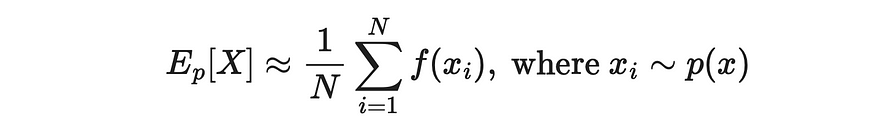
通过部分总和进行期望值估计。X 的值是从 p(x) 分布中采样的。来源:强化学习。引言。第二版 |Richard S. Sutton 和 Andrew G. Barto
5.2 想法
重要性抽样的思想是通过一个变量(目标策略)的分布来估计另一个变量(目标策略)的期望值。我们可以将另一个分布表示为 q。通过使用简单的数学逻辑,让我们推导出 p 到 q 的期望值的公式:
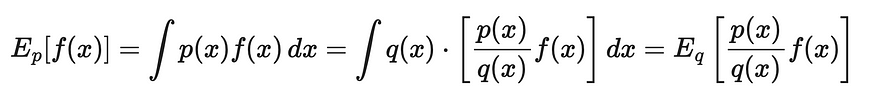
一个分布的预期值通过另一个分布的表示值来表示。来源:强化学习。引言。第二版 |Richard S. Sutton 和 Andrew G. Barto
因此,我们可以以部分和的形式重写最后一个表达式,并使用它来计算原始期望值。
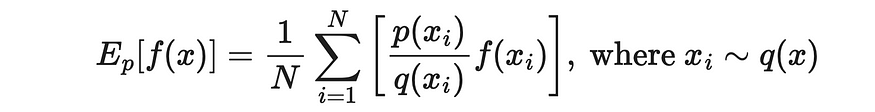
X 的值是从 q(x) 分布中采样的。来源:强化学习。引言。第二版 |Richard S. Sutton 和 Andrew G. Barto
这个结果的奇妙之处在于,现在 x 的值是从新的分布中采样的。如果从 q 采样比 p 更快,那么我们的估计效率就会得到显著提高。
5.3 应用
最后一个推导的公式非常适合非策略方法!为了更清楚地说明,让我们了解它的每一个单独组成部分:
- Ep[f(x)] 是目标策略下的平均回报 G π我们想最终估计给定状态 s 的 G。
- x 对应于我们要估计其返回值的单个状态 S;习 是通过状态 S 的 N 个轨迹(观测值)之一。
- f(习) 是状态 s 的返回 G。
- p(习) 是保单 π 下获得回报 G 的概率。
- q(习) 是在策略 b 下获得回报 G 的概率。
由于采样数据只能通过策略 b 获得,因此在公式表示法中,我们不能使用 x ~ p(x)(我们只能使用 x ~ q(x))。这就是为什么使用重要性抽样是有意义的。
但是,要将重要性抽样应用于 MC 方法,我们需要稍微修改最后一个公式。
- 回想一下,我们的目标是计算策略 π下的 Q-函数。
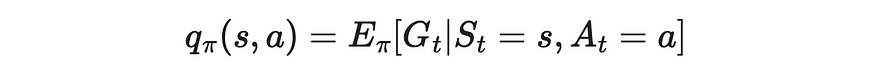
目标策略下的 q 值定义。来源:强化学习。引言。第二版 |Richard S. Sutton 和 Andrew G. Barto
2. 在 MC 方法中,我们估计策略 b 下的 Q 函数。

行为策略下的 q 值定义。来源:强化学习。引言。第二版 |Richard S. Sutton 和 Andrew G. Barto
3. 我们使用重要性抽样公式来估计策略 π 下通过策略 b 的 Q 函数。
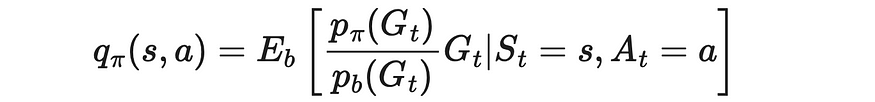
重要性采样公式在 Monte Carlo 算法中的应用。来源:强化学习。引言。第二版 |Richard S. Sutton 和 Andrew G. Barto
4. 我们必须计算给定当前状态 s 和代理的下一个动作 a 获得奖励 G 的概率。让我们用 t 表示代理最初处于状态 s 的开始时刻。T 是当前剧集结束时的最终时间戳。

获得奖励 G 的概率可以表示为转换概率的乘积。
那么期望的概率可以表示为代理体在这一集中具有从 st 到终末状态的轨迹的概率。这个概率可以写成代理在给定策略(π 或 b)下采取某种行动导致其进入轨迹中下一个状态的概率和转换概率 p 的序列乘积。
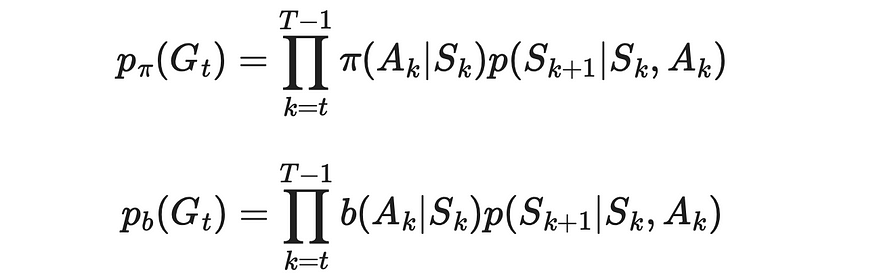
获得回报 Gt 的概率。来源:强化学习。引言。第二版 |Richard S. Sutton 和 Andrew G. Barto
5. 尽管我们不知道转换概率,但我们不需要它们。由于我们必须将 π 下的 p(Gt) 与 b 下的 p(Gt) 进行除法,因此分子和分母中都存在的转换概率将消失。
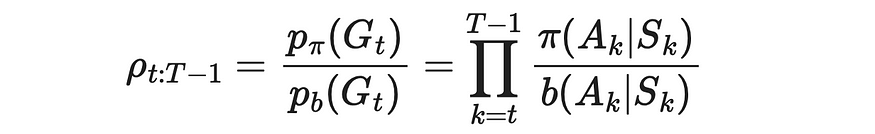
重要性抽样比率。来源:强化学习。引言。第二版 |Richard S. Sutton 和 Andrew G. Barto
得到的比率 ρ 称为重要性-采样比率。
6. 将计算出的比率代入原始公式中,以获得策略 π 下 Q-函数的最终估计值。
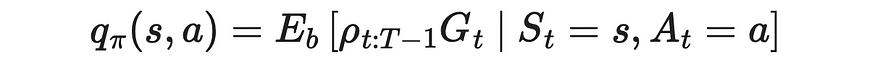
目标策略下 q 值通过重要性采样率的公式。来源:强化学习。引言。第二版 |Richard S. Sutton 和 Andrew G. Barto
如果我们需要计算 V 函数,结果将是类似的:
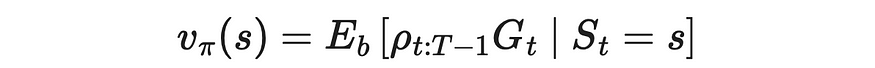
目标策略下 v 值通过重要性采样率的公式。来源:强化学习。引言。第二版 |Richard S. Sutton 和 Andrew G. Barto
我们之前看到的 blackjack 实现是一种 on-policy 算法,因为在数据采样和策略改进期间使用相同的策略。
六、增量实施
6.1 增量的理论
我们可以做的另一件事来改进 MC 实现,即使用增量实现。在上面给定的伪代码中,我们必须定期重新计算 state-action 值的平均值。以数组的形式存储给定对 (S, A) 的返回值,并在向数组添加新的返回值时使用它来重新计算 avreage 是低效的。
相反,我们可以做的是将 average 公式写成递归形式:
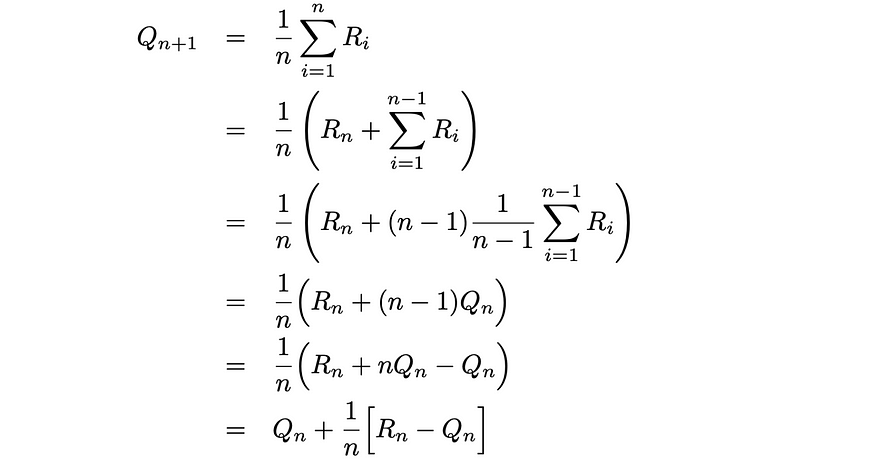
用于平均值计算的递归公式。Ri 代表第 i 个奖励,而 Qi 是第一个 i-1 奖励的平均值。来源:强化学习。引言。第二版 |Richard S. Sutton 和 Andrew G. Barto
获得的公式让我们有机会将当前平均值更新为前一个平均值和新回报的函数。通过使用这个公式,我们每次迭代的计算都需要恒定的 O(1) 时间,而不是线性的 O(n) 通过数组。此外,我们不再需要存储数组。
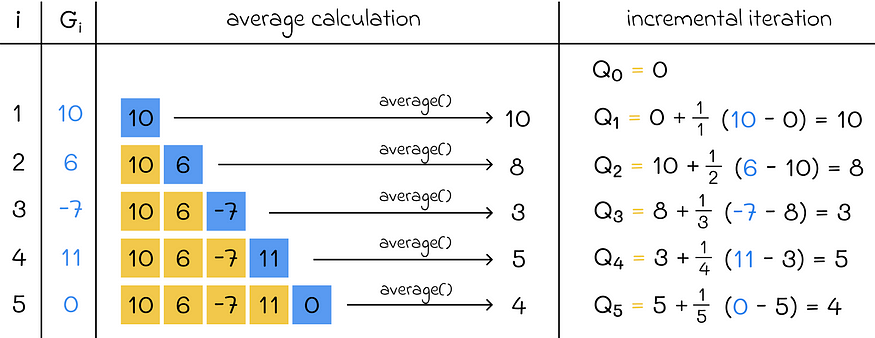
朴素平均计算和增量迭代之间的比较示例。
增量实现还用于许多其他算法,这些算法会在新数据可用时定期重新计算平均值。
6.2 常α MC
如果我们遵守上面的更新规则,我们可以注意到术语 1 / n 是一个常数。我们可以通过引入 α 参数来替换 1 / n,该参数可以自定义设置为介于 0 和 1 之间的正值。
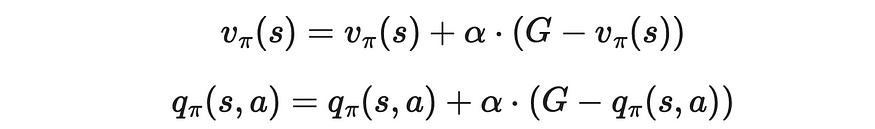
更新 constant-alpha MC 中的规则
使用 α 参数,我们可以控制下一个观测值对先前值的影响。此调整也会影响收敛过程:
- 较小的 α 值会使算法收敛到真实答案的速度较慢,但一旦估计的平均值位于真实平均值附近,则会导致较低的方差;
- α值越大,算法收敛到真实答案的速度就越快,但一旦估计的平均值位于真实平均值附近,则会导致更高的方差。
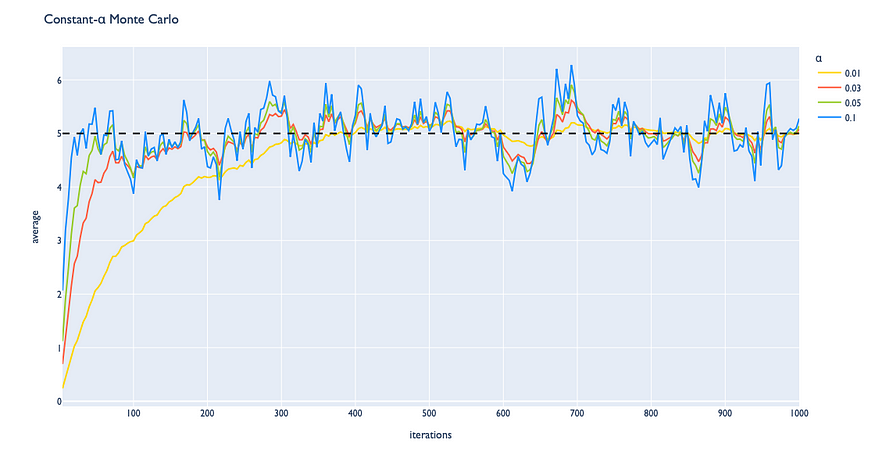
常数α MC 算法如何根据所选的 α 值以不同的方式收敛的示例。
七、结论
最后,我们了解了 on-policy 和 off-policy 方法之间的区别。虽然非政策方法通常更难进行适当调整,但它们提供了更好的策略。作为调整目标策略值的示例的重要性抽样是强化学习中的关键技术之一,用于大多数非策略方法。