一、01背包理论基础
例题:46. 携带研究材料
01 背包
有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大。
暴力解法:每个物品有取或不取两种状态,可以用回溯法遍历,时间复杂度O(2^n)
时间复杂度是指数级别,考虑动态规划进行优化。
动规五部曲:
1.确定dp数组及下标含义
需要使用二维数组,因为有两个维度需要考虑:物品、背包容量

dp[i][j] 表示从下标为[0-i]的物品里任意取,放进容量为j的背包,价值总和最大是多少。
2.确定递推公式
dp[i][j]的来源:
-
不放物品i:由dp[i - 1][j]推出,即背包容量为j,里面不放物品i的最大价值,此时dp[i][j]就是dp[i - 1][j]。
-
放物品i:由dp[i - 1][j - weight[i]]推出,dp[i - 1][j - weight[i]] 为背包容量为j - weight[i]的时候不放物品i的最大价值,那么dp[i - 1][j - weight[i]] + value[i] (物品i的价值),就是背包放物品i得到的最大价值
dp[i][j] = Math.max( dp[i-1][j] , dp[i-1][j-w[i]] + v[i] )
3.dp数组初始化
要初始化那些部分,要从递推方程来看,从递推方程可以看到dp[i][j]来源于 dp[i-1]行,所以dp[0]行要初始化:
dp[0][j],即:i为0,存放编号0的物品的时候,各个容量的背包所能存放的最大价值。
那么很明显当 j < weight[0]的时候,dp[0][j] 应该是 0,因为背包容量比编号0的物品重量还小。
当j >= weight[0]时,dp[0][j] 应该是value[0],因为背包容量放足够放编号0物品。
同时,从dp数组定义出发,容量为0时候,最大价值为0;只考虑第0种物品时,能够放得下则初始化为value[0].
4.确定遍历顺序
先遍历 物品还是先遍历背包重量呢?
其实都可以!! 但是先遍历物品更好理解。
先给出先遍历物品,然后遍历背包重量的代码。
// weight数组的大小 就是物品个数
for(int i = 1; i < weight.size(); i++) { // 遍历物品
for(int j = 0; j <= bagweight; j++) { // 遍历背包容量
if (j < weight[i]) dp[i][j] = dp[i - 1][j];
else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
}
}先遍历背包,再遍历物品,也是可以的!(注意我这里使用的二维dp数组)
例如这样:
// weight数组的大小 就是物品个数
for(int j = 0; j <= bagweight; j++) { // 遍历背包容量
for(int i = 1; i < weight.size(); i++) { // 遍历物品
if (j < weight[i]) dp[i][j] = dp[i - 1][j];
else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
}
}要理解递归的本质和递推的方向。
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); 递归公式中可以看出dp[i][j]是靠dp[i-1][j]和dp[i - 1][j - weight[i]]推导出来的。
dp[i-1][j]和dp[i - 1][j - weight[i]] 都在dp[i][j]的左上角方向(包括正上方向),那么先遍历物品,再遍历背包的过程如图所示:
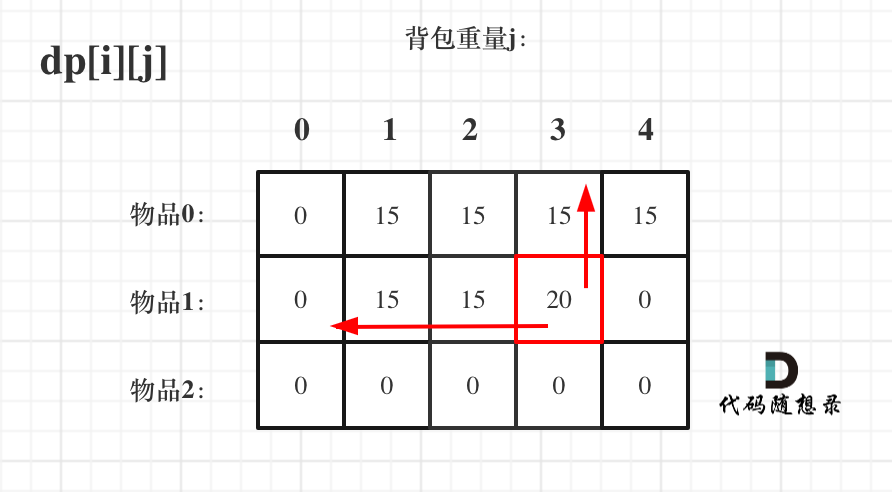
再来看看先遍历背包,再遍历物品呢,如图:
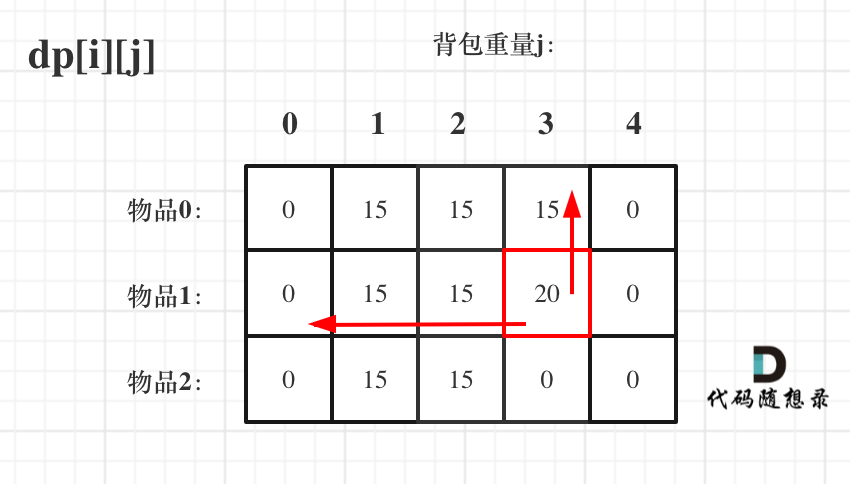
大家可以看出,虽然两个for循环遍历的次序不同,但是dp[i][j]所需要的数据就是左上角,根本不影响dp[i][j]公式的推导!
但先遍历物品再遍历背包这个顺序更好理解。
5.举例推导dp数组
来看一下对应的dp数组的数值,如图:
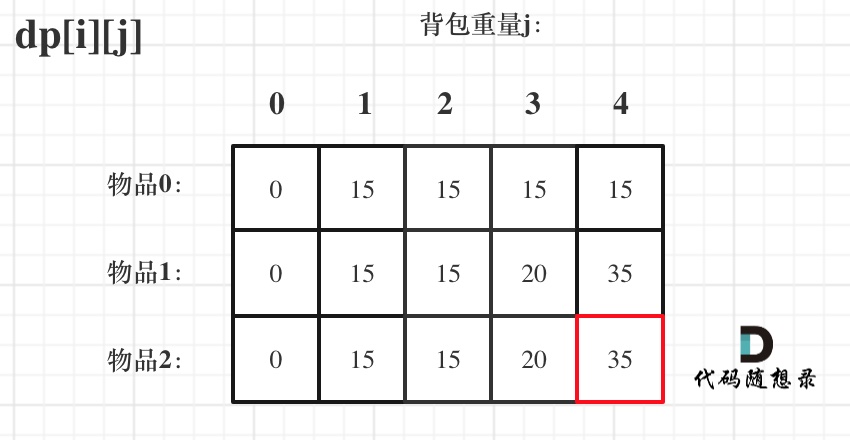
最终结果就是dp[2][4]。
代码如下:
import java.util.Scanner;
public class Main{
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int capacity = scanner.nextInt();
int[] value = new int[n];
int[] weight = new int[n];
for(int i = 0; i < n ; i++){
weight[i] = scanner.nextInt();
}
for(int i = 0; i < n ; i++){
value[i] = scanner.nextInt();
}
int[][] dp = new int[n][capacity+1];
for(int i = 0 ; i < n ; i++){
dp[i][0] = 0;
}
for(int j = 0; j <=capacity ; j++){
if(j >= weight[0]){
dp[0][j] = value[0];
}
}
for(int i = 1; i < n ; i++){
for(int j = 0; j <= capacity ; j++){
if(j < weight[i]){
dp[i][j] = dp[i-1][j];
}else{
dp[i][j] = Math.max(dp[i-1][j],dp[i-1][j-weight[i]]+value[i]);
}
}
}
System.out.println(dp[n-1][capacity]);
}
}关于滚动数组
对于背包问题其实状态都是可以压缩的。
在使用二维数组的时候,递推公式:dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
其实可以发现如果把dp[i - 1]那一层拷贝到dp[i]上,表达式完全可以是:dp[i][j] = max(dp[i][j], dp[i][j - weight[i]] + value[i]);
与其把dp[i - 1]这一层拷贝到dp[i]上,不如只用一个一维数组了,只用dp[j](一维数组,也可以理解是一个滚动数组)
这就是滚动数组的由来,需要满足的条件是上一层可以重复利用,直接拷贝到当前层。
动规五部曲分析如下:
1.确定dp数组及下标含义
在一维dp数组中,dp[j]表示:容量为j的背包,所背的物品价值可以最大为dp[j]。
2.递推公式
二维dp数组的递推公式为: dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
一维dp数组,其实就上上一层 dp[i-1] 这一层 拷贝的 dp[i]来。
所以在 上面递推公式的基础上,去掉i这个维度就好。
递推公式为:dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
分析:
dp[j]为 容量为j的背包所背的最大价值。
dp[j]可以通过dp[j - weight[i]]推导出来,dp[j - weight[i]]表示容量为j - weight[i]的背包所背的最大价值。
dp[j - weight[i]] + value[i] 表示 容量为 [j - 物品i重量] 的背包 加上 物品i的价值。(也就是容量为j的背包,放入物品i了之后的价值即:dp[j])
此时dp[j]有两个选择,一个是取自己dp[j] 相当于 二维dp数组中的dp[i-1][j],即不放物品i,一个是取dp[j - weight[i]] + value[i],即放物品i,指定是取最大的,毕竟是求最大价值,
所以递归公式为:
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);3.初始化
初始化,一定要和dp数组的定义吻合。
dp[j]表示:容量为j的背包,所背的物品价值可以最大为dp[j],那么dp[0]就应该是0,因为背包容量为0所背的物品的最大价值就是0。
那么dp数组除了下标0的位置,初始为0,其他下标应该初始化多少呢?
看一下递归公式:dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
dp数组在推导的时候一定是取价值最大的数,如果题目给的价值都是正整数那么非0下标都初始化为0就可以了。
这样才能让dp数组在递归公式的过程中取的最大的价值,而不是被初始值覆盖了。
那么我假设物品价值都是大于0的,所以dp数组初始化的时候,都初始为0就可以了。
4.遍历顺序
for(int i = 0; i < weight.size(); i++) { // 遍历物品
for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
}二维dp遍历的时候,背包容量是从小到大,而一维dp遍历的时候,背包是从大到小。
为什么呢?
倒序遍历是为了保证物品i只被放入一次!。但如果一旦正序遍历了,那么物品0就会被重复加入多次!
举一个例子:物品0的重量weight[0] = 1,价值value[0] = 15
如果正序遍历
dp[1] = dp[1 - weight[0]] + value[0] = 15
dp[2] = dp[2 - weight[0]] + value[0] = 30
此时dp[2]就已经是30了,意味着物品0,被放入了两次,所以不能正序遍历。
为什么倒序遍历,就可以保证物品只放入一次呢?
倒序就是先算dp[2]
dp[2] = dp[2 - weight[0]] + value[0] = 15 (dp数组已经都初始化为0)
dp[1] = dp[1 - weight[0]] + value[0] = 15
所以从后往前循环,每次取得状态不会和之前取得状态重合,这样每种物品就只取一次了。
为什么二维dp数组遍历的时候不用倒序呢?
因为对于二维dp,dp[i][j]都是通过上一层即dp[i - 1][j]计算而来,本层的dp[i][j]并不会被覆盖!
(也就是说,根据递推公式,计算后面的要用到前面的,因此前面的要后算,从后往前算)
再来看看两个嵌套for循环的顺序,代码中是先遍历物品嵌套遍历背包容量,那可不可以先遍历背包容量嵌套遍历物品呢?
不可以!
因为一维dp的写法,背包容量一定是要倒序遍历(原因上面已经讲了),如果遍历背包容量放在上一层,那么每个dp[j]就只会放入一个物品,即:背包里只放入了一个物品。
所以一维dp数组的背包在遍历顺序上和二维其实是有很大差异的!,这一点大家一定要注意。

5.举例推导dp数组
一维dp,分别用物品0,物品1,物品2 来遍历背包,最终得到结果如下:
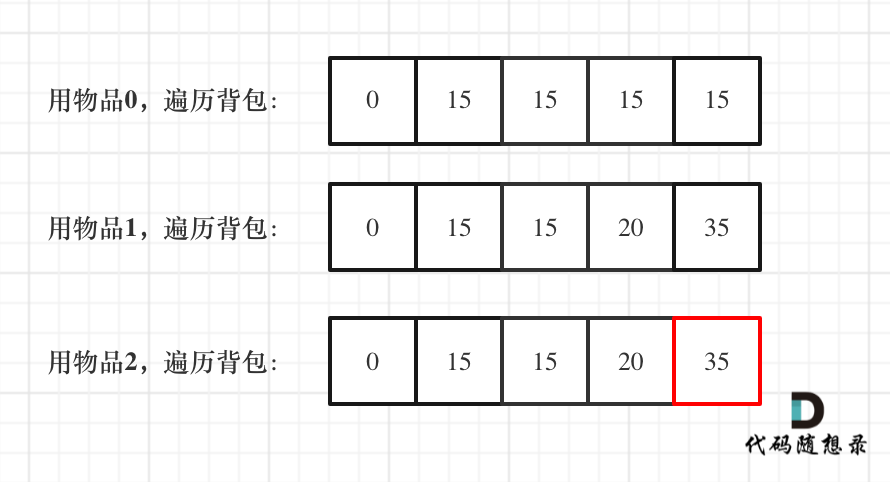
二、习题
1.416. 分割等和子集
可以用回溯法,但是会超时(剪枝了也超时):
class Solution {
int[] nums;
int sum ;
int tmpSum;
boolean flag = false;
public boolean canPartition(int[] nums) {
this.nums = nums;
sum = Arrays.stream(nums).sum();
if(sum%2 == 1) return false;
dfs(0);
if(flag) return true;
return false;
}
public void dfs(int startIndex){
if(tmpSum == sum/2){
flag = true;
return ;
}
if(startIndex == nums.length ){
return;
}
for(int i = startIndex ; i < nums.length ; i++){
tmpSum += nums[i];
dfs(i+1);
tmpSum -= nums[i];
}
}
}考虑动态规划
背包问题有多种背包方式,常见的有:01背包、完全背包、多重背包、分组背包和混合背包等等。
要注意题目描述中商品是不是可以重复放入。
即一个商品如果可以重复多次放入是完全背包,而只能放入一次是01背包,写法还是不一样的。
要明确本题中我们要使用的是01背包,因为元素我们只能用一次。
本题要求集合里能否出现总和为 sum / 2 的子集。
那么来一一对应一下本题,看看背包问题如何来解决。
只有确定了如下四点,才能把01背包问题套到本题上来。
- 背包的体积为sum / 2
- 背包要放入的商品(集合里的元素)重量为 元素的数值,价值也为元素的数值
- 背包如果正好装满,说明找到了总和为 sum / 2 的子集。
- 背包中每一个元素是不可重复放入。
动规五部曲分析如下:
1.确定dp数组以及下标的含义
01背包中,dp[j] 表示: 容量为j的背包,所背的物品价值最大可以为dp[j]。
2.确定递推公式
if(j < nums[i]) dp[i][j] = dp[i-1][j];
else dp[i][j] = Math.max(dp[i-1][j],dp[i-1][j-nums[i]]+nums[i]);3.dp数组初始化
for(int j = nums[0] ; j <= target ; j++) dp[0][j] = nums[0];这里要考虑nums元素是否非负,如果有负数,则dp[i][0] 要初始化为Integer.MIN_VALUE
dp[0][j]初始化为0
4.遍历顺序
从上到下,从左到右
5.模拟dp数组
代码如下:
class Solution {
public boolean canPartition(int[] nums) {
int sum = Arrays.stream(nums).sum();
if(sum % 2 == 1) return false;
int target = sum/2;
//dp[i][j] 考虑前i个数,capacity = j 所能装的最大value
int[][] dp = new int[nums.length][target+1];
for(int j = nums[0] ; j <= target ; j++) dp[0][j] = nums[0];
for(int i = 1; i < nums.length ; i++){
for(int j = 1 ; j <= target ; j++){
if(j < nums[i]) dp[i][j] = dp[i-1][j];
else dp[i][j] = Math.max(dp[i-1][j],dp[i-1][j-nums[i]]+nums[i]);
}
}
if(dp[nums.length-1][target] == target) return true;
return false;
}
}滚动数组优化,注意初始化、嵌套顺序要求先遍历物品种类、容量倒序遍历:
class Solution {
public boolean canPartition(int[] nums){
int sum = Arrays.stream(nums).sum();
if(sum % 2 == 1) return false;
int target = sum/2;
//dp[j]表示容量j下能装入的最大价值
int[] dp = new int[target+1];
//初始化
//遍历
for(int i = 0; i < nums.length ; i++){
for(int j = target ; j >= nums[i] ; j--){
dp[j] = Math.max(dp[j],dp[j-nums[i]]+nums[i]);
}
}
if(dp[target] == target) return true;
return false;
}
}总结
这道题目就是一道01背包应用类的题目,需要我们拆解题目,然后套入01背包的场景。
01背包相对于本题,主要要理解,题目中物品是nums[i],重量是nums[i],价值也是nums[i],背包体积是sum/2。
2.1049.最后一块石头的重量II
本题其实就是尽量让石头分成重量相同的两堆,相撞之后剩下的石头最小,这样就化解成01背包问题了。
本题物品的重量为stones[i],物品的价值也为stones[i]。
本题的目的是划分两个子集,使这两个子集和 的 差最小,可以转化为动态规划01背包问题。
1.dp数组及下标含义
dp[j]表示容量为j的背包能够装的最大价值,这里价值设定为=重量,也即容量为j的背包能够装的最大重量
2.递推公式
dp[j] = Math.max( dp[j] , dp[j - stones[i] ] + stones[i])
3.初始化
stones[i] > 0 ,初始化0即可
4.遍历顺序
外层物品,内层容量,内层逆序
5.模拟dp
举例,输入:[2,4,1,1],此时target = (2 + 4 + 1 + 1)/2 = 4 ,dp数组状态图如下:
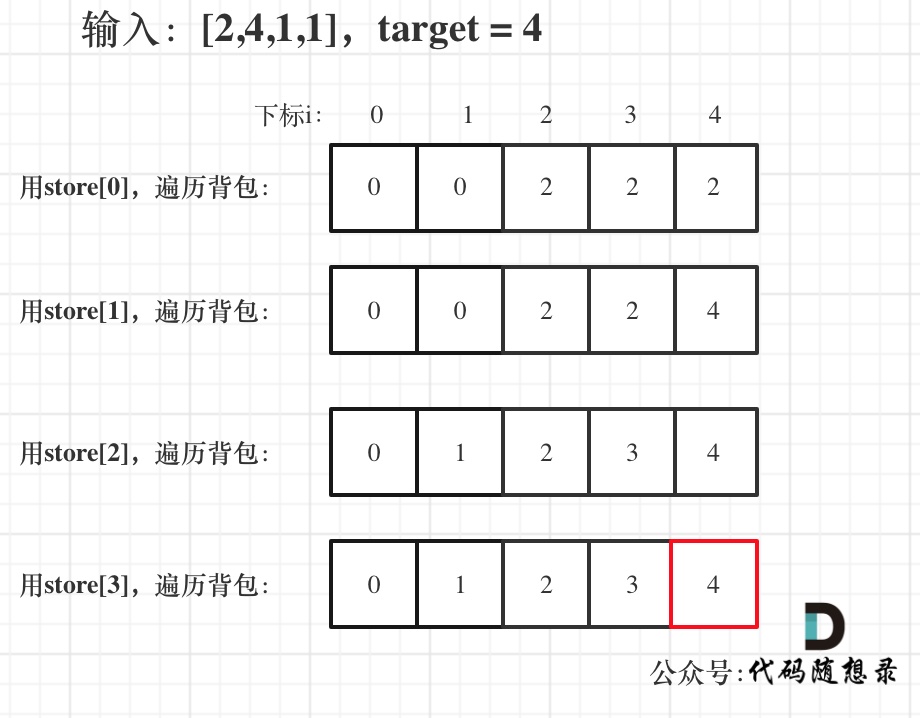
最后dp[target]里是容量为target的背包所能背的最大重量。
那么分成两堆石头,一堆石头的总重量是dp[target],另一堆就是sum - dp[target]。
在计算target的时候,target = sum / 2 因为是向下取整,所以sum - dp[target] 一定是大于等于dp[target]的。
那么相撞之后剩下的最小石头重量就是 (sum - dp[target]) - dp[target]。
代码如下:
class Solution {
public int lastStoneWeightII(int[] stones) {
int sum = Arrays.stream(stones).sum();
int target = sum/2;
int[] dp = new int[target+1];
for(int i = 0; i < stones.length ; i++){
for(int j = target ; j >= stones[i] ; j--){
dp[j] = Math.max(dp[j], dp[j-stones[i]]+stones[i]);
}
}
return sum - dp[target] - dp[target];
}
}总结
本题其实和416. 分割等和子集几乎是一样的,只是最后对dp[target]的处理方式不同。
416. 分割等和子集 相当于是求背包是否正好装满,而本题是求背包最多能装多少。
3.494.目标和
回溯法,时间复杂度O(2^nums.length)
class Solution {
int sum = 0;
int result = 0;
int[] nums;
int target = 0;
public int findTargetSumWays(int[] nums, int target) {
this.nums = nums;
this.target = target;
dfs(0);
return result;
}
public void dfs(int startIndex){
if(startIndex == nums.length){
if(sum == target){
result++;
}
return ;
}
target += nums[startIndex];
dfs(startIndex+1);
target -= nums[startIndex];
target-=nums[startIndex];
dfs(startIndex+1);
target += nums[startIndex];
}
}动态规划
本题要如何使表达式结果为target,
既然为target,那么就一定有 left组合 - right组合 = target。
left + right = sum,而sum是固定的。right = sum - left
公式来了, left - (sum - left) = target 推导出 left = (target + sum)/2 。
target是固定的,sum是固定的,left就可以求出来。
此时问题就是在集合nums中找出和为left的组合。
问题转化为,装满容量为x的背包,有几种方法。
注意:
sum + target 为奇数,无解
(C++代码中,输入的S 就是题目描述的 target)
if ((target + sum) % 2 == 1) return 0; // 此时没有方案
同时如果target 的绝对值已经大于sum,无解
if (abs(target) > sum) return 0; // 此时没有方案动态规划五部曲:
1.dp数组及下标含义:
dp[j] :填满容量为j的背包有dp[j]种方法
2.确定递推数组
确定一个nums[i] , 就有 dp[ j - nums[i] ] 种方法,那么对每一个 nums[i] 累加 dp[j-nums[i]]即可
求组合类问题的公式,都是类似这种:
dp[j] += dp[j - nums[i]]3.dp数组初始化

or
![]()
4.遍历顺序
先物品种类,再容量,容量逆序
5.模拟dp
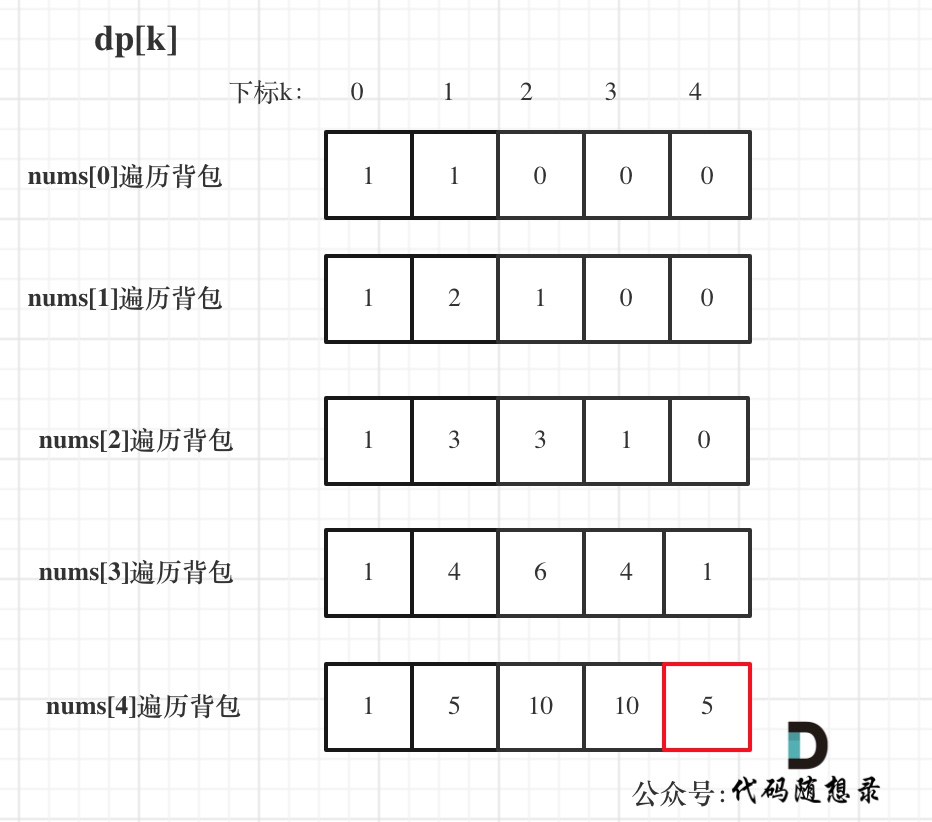
输入:nums: [1, 1, 1, 1, 1], target: 3
bagSize = (target + sum) / 2 = (3 + 5) / 2 = 4
dp数组状态变化如下:
当思路不清晰时先用二维数组做:

滚动数组的外层for循环的i代表的是“考虑前i个数字”而不是“考虑第i个数字”
4.474.一和零
本题是二维01背包问题。
特殊的是遍历物品(字符串)的时候,先对字符串进行处理,得到单个物品的重量和体积。要求的是最大子集,因此希望物品越多越好,物品价值均设1.
1.dp数组及下标含义
dp[i][j][k]:表示考虑前i个字符串,重量为j,体积为k时最多能装入的字符串
2.递推公式
dp[i][j][k] = Math.max ( dp[i-1][j][k] , dp[i-1][j - zeroNum][ k - oneNum] + 1 )
3.初始化
第0个物品, 对 j >= zeroNum && k >=oneNum , dp[i][j][k]赋1
4.遍历顺序
最外层是物品种类,内层是重量和体积
5.dp模拟
代码如下:
class Solution {
public int findMaxForm(String[] strs, int m, int n) {
int[][][] dp = new int[strs.length][m+1][n+1];
int zero = 0 , one = 0;
for(char c : strs[0].toCharArray()){
if(c == '0') zero++;
else one++;
}
for(int j = m ; j >= zero ; j--){
for(int k = n ; k >= one ; k--){
dp[0][j][k] = 1;
}
}
for(int i = 1; i < strs.length ; i++){
int zeroNum = 0 , oneNum = 0;
for(char c : strs[i].toCharArray()){
if(c == '0') zeroNum++;
else oneNum++;
}
for(int j = 0 ; j <= m ; j++){
for(int k = 0; k <= n ; k++){
if(j < zeroNum || k < oneNum) dp[i][j][k] = dp[i-1][j][k];
else dp[i][j][k] = Math.max(dp[i-1][j][k], dp[i-1][j-zeroNum][k-oneNum] + 1);
}
}
}
return dp[strs.length-1][m][n];
}
}滚动数组优化:
1.dp数组及下标含义:
dp[i][j] : 当前正在遍历的前k种物品中,重量限制为i、体积限制为j的背包最多能够装下多少个物品(字符串)
2.递推公式
dp[i][j] = Math.max(dp[i][j] , dp[i-zereNum][j-oneNum] + 1)
3.初始化
仅考虑第0种物品(第一个元素), 对dp数组 i >= zeroNum, j >=oneNum的元素赋1(第0种物品的价值)
这之后从第1个物品开始动态规划
or

4.遍历顺序
最外层是物品种类,内层分别是重量和体积,重量和体积均逆序
5.dp模拟
以输入:["10","0001","111001","1","0"],m = 3,n = 3为例
最后dp数组的状态如下所示:
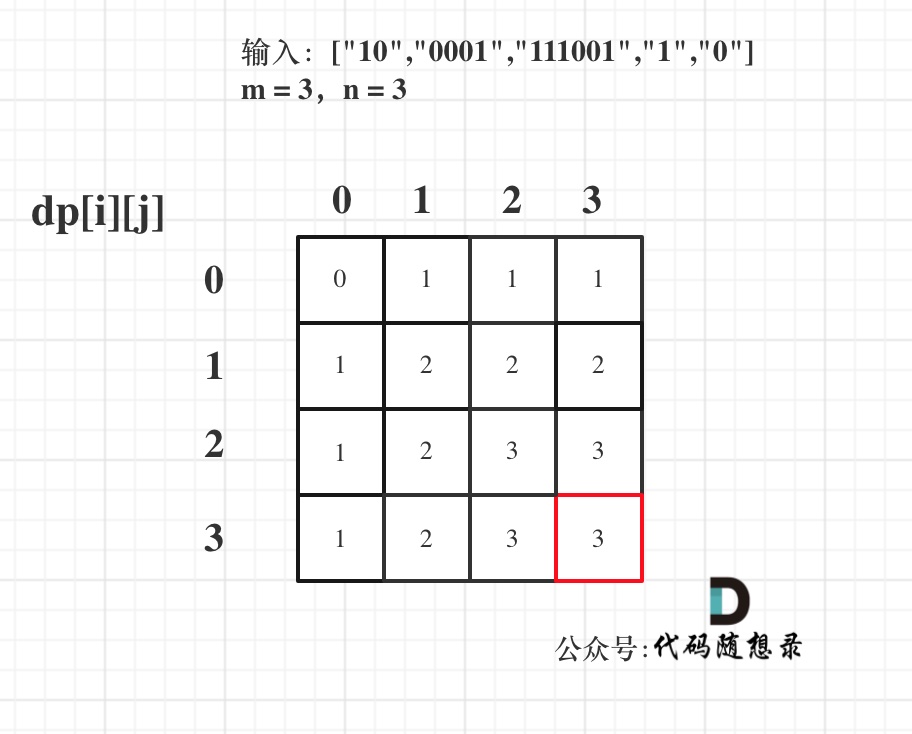
代码如下:
class Solution {
public int findMaxForm(String[] strs, int m, int n) {
int[][] dp = new int[m+1][n+1];
int zero = 0, one = 0;
for(char c : strs[0].toCharArray()){
if(c == '0') zero++;
else one++;
}
for(int i = m ; i >= zero ; i--){
for(int j = n ; j >= one ; j--){
dp[i][j] = 1;
}
}
for(int k = 1 ; k < strs.length ; k++){
int zeroNum = 0, oneNum = 0;
for(char c : strs[k].toCharArray()){
if(c == '0') zeroNum++;
else oneNum++;
}
for(int i = m ; i >= zeroNum ; i--){
for(int j = n ; j >= oneNum ; j--){
dp[i][j] = Math.max(dp[i][j] , dp[i-zeroNum][j-oneNum]+1);
}
}
}
return dp[m][n];
}
}总结
不少同学刷过这道题,可能没有总结这究竟是什么背包。
此时我们讲解了0-1背包的多种应用,
- 纯 0 - 1 背包 是求 给定背包容量 装满背包 的最大价值是多少。
- 416. 分割等和子集是求 给定背包容量,能不能装满这个背包。
- 1049. 最后一块石头的重量 II是求 给定背包容量,尽可能装,最多能装多少
- 494. 目标和是求 给定背包容量,装满背包有多少种方法。
- 本题是求多维背包背景下,尽可能装满背包最多有多少个物品。
在代码随想录中所列举的题目,都是 0-1背包不同维度上的应用。