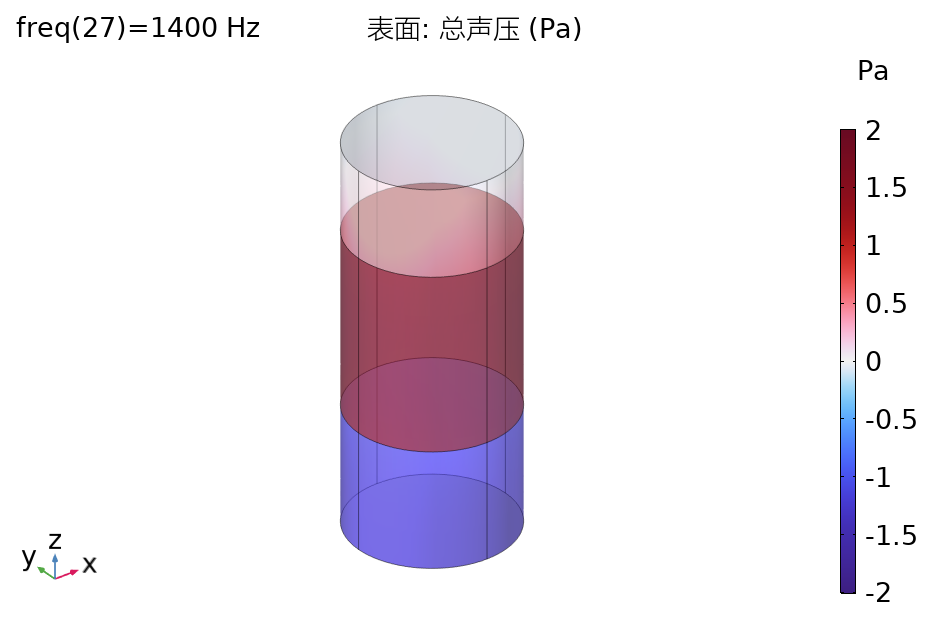
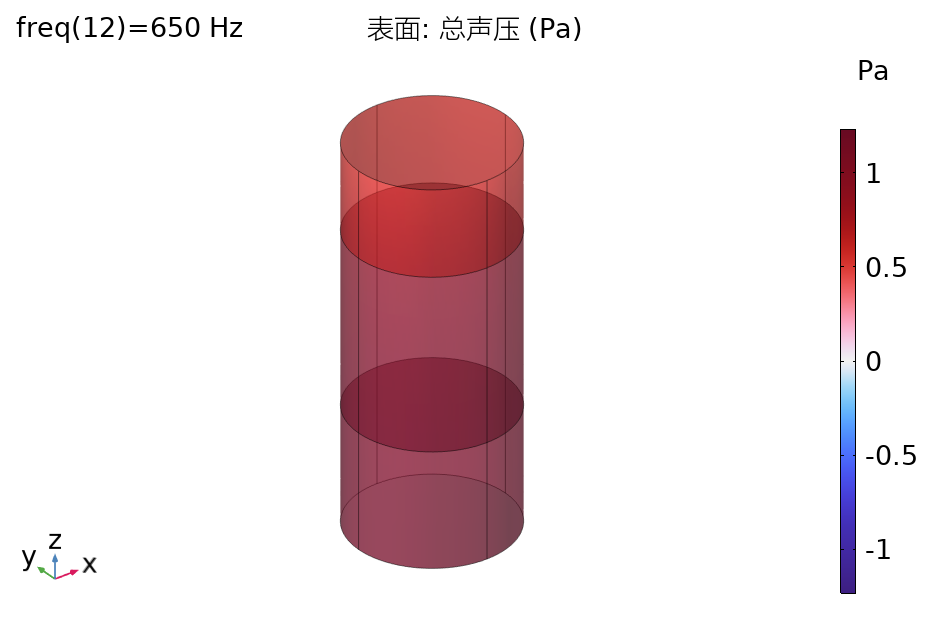
微穿孔板吸声体是由穿孔直径在1毫米以下的薄板和板后空腔组成的共振吸声结构。与传统的吸声材料及普通穿孔板吸声体相比,微穿孔板吸声体清洁,可收回重复利用,不燃,坚固,重量轻,由于不需另加纤维等多孔性吸声材料即可获得良好的吸声性能,且制造不受材料限制,不污染环境,已成功应用在建筑物内部,消声器,轮船等众多领域,被誉为新一代最吸引人的吸声材料。
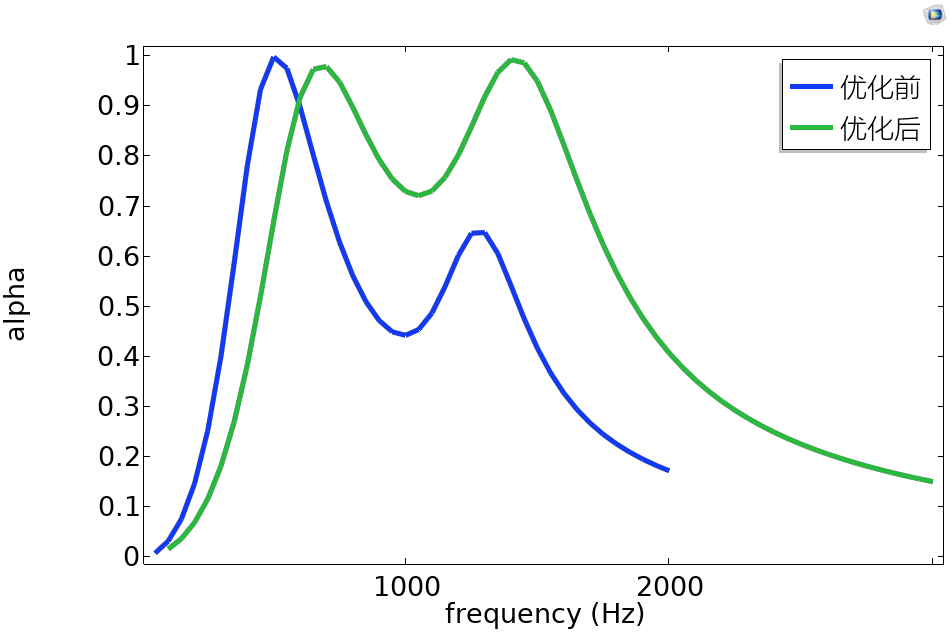
微穿孔板吸声体的吸声性能主要取决于自身的结构参数,合理的参数组合会获得很好的吸声效果,然而通过穷举搜索较优的参数组合是不切实际的,更好的方法是采用优化算法。经典的微穿孔板吸声体理论模型假设穿孔的板是刚性的,忽略了板自身材料性能对微穿孔板吸声体吸声特性的影响,但是当这种影响不可忽略时,该模型的精确度降低。本文重点围绕微穿孔板吸声体结构参数的优化设计与计算机仿真方面展开相关的研究。


-
模型构建

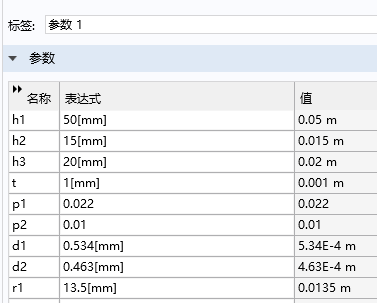
-
网格划分

-
边界条件与求解器
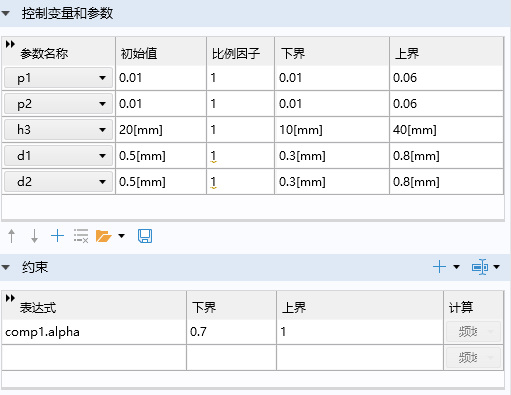
利用comsol优化模块进行结构参数优化,Comsol优化功能的求解器有:
-
SNOPT: 鲁棒性、基于梯度、通用的、连续二次规划法求解非线性约束问题。
-
MMA: 通用的、基于连续凸近似的内点法根据对象和约束的梯度信息构建,特别适合拓扑优化问题。
-
Levenberg-Marquardt: 最小二乘拟合专属求解器,使用特殊问题结构通过一阶梯度数据计算二阶导数忽略约束。
-
Nelded-Mead: 鲁棒性强、无梯度、启发式、单纯形搜索算法,包括对约束处理的补偿法。
-
BOBYQA: 对目标函数样的算法,构建和控制在移动置信区间目标的二次近似。使用增广拉格朗日封装器处理一般约束,求解一系列无约束问题。
-
COBYLA: 对目标函数和约束变量抽样算法,构建和控制在移动置信区间内目标的线性近似支持一般约束,但可能在中间解步骤中不满足约束。
-
Coordinate search 坐标搜索: 沿控制变量轴连续抽样,寻找最优的方法,主要特点是每次改变一个控制变量。
-
Monte Carlo 蒙特卡罗基本的随机抽样算法,用于探索设计空间,提取统计信息。