数字信号处理的领域中,时域是我们理解和处理数字信号的关键维度之一。
时域分析能够让我们直接观察信号随时间的变化情况,为后续的信号处理和系统设计提供坚实的基础。
接下来将以通俗易懂的方式,让大家深入了解数字信号处理基础中的时域概念。
一、时域的基本概念
时域是描述数学函数或物理信号对时间的关系。
在时域中,信号是时间的函数,以时间为轴线,以时间为标尺来展示信号的变化。
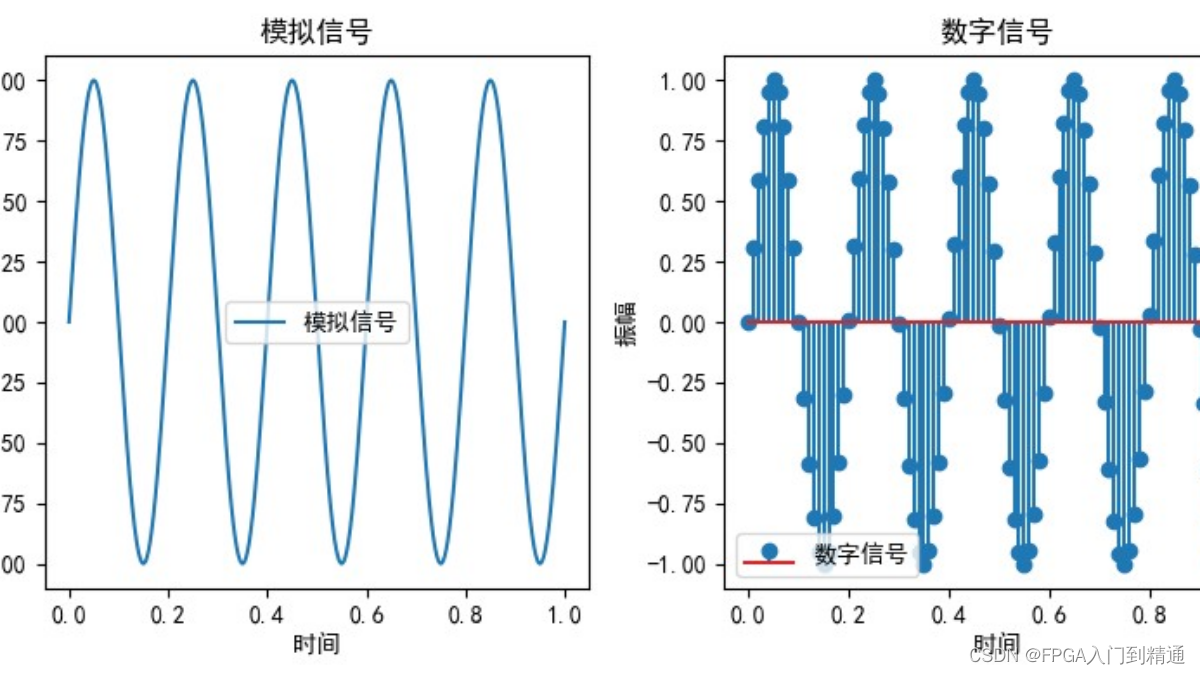
对于连续时间信号,时间变量是连续的,函数或信号在任意时间的数值均为已知;
对于离散时间信号,时间变量是离散的整数,信号在各个离散时间点上有对应的数值。
时域的表示较为形象与直观,能够直接反映信号随时间的波动、持续时间、变化趋势等特征。
二、时域中的重要参数
1、周期
对于周期性信号,周期是指信号完成一个完整波形所需要的时间,常用T表示。
比如常见的交流电信号,其周期通常为 0.02 秒(对应频率为 50Hz),这意味着每 0.02 秒电流或电压完成一个完整的变化周期。
2、频率
频率是周期的倒数,表示单位时间内信号完成的周期数,常用f表示。
频率越高,信号变化越快。
例如,高频的音频信号能够传达更丰富的声音细节。人类可听到的声音频率范围大约在 20Hz 到 20kHz 之间。
3、 峰值
信号在一段时间内的最大值,反映了信号的最大强度。
比如一个音频信号的峰值可能达到一定的电压值,如 10V。
4、均值
信号所有取值的平均,它代表了信号的直流分量,体现了信号在时间上的中心趋势。
5、均方值
表示信号强度,其平方根为有效值(RMS),常用于衡量信号的功率大小。
6、方差
用于反映信号绕均值的波动程度,方差越大,说明信号的波动越剧烈。
三、时域信号的表示方法
1、函数表达式
连续时间信号用 x(t),如正弦信号 x(t)=A*sin(ωt + φ);
离散时间信号用 x(n),如指数序列 x(n)=a^n。
2、图形表示
连续时间信号以连续曲线在二维坐标(横轴 t、纵轴 x(t))表示;
离散时间信号以离散点在二维坐标(横轴 n、纵轴 x(n))表示。
3、集合符号表示
离散时间信号可表示为 x(n)={值列表 ; n=时间点列表}。
x(n)={1, 2, 3, 4, 3, 2, 1 ; n=0,1,2,3,4,5,6}
四、常用的典型序列
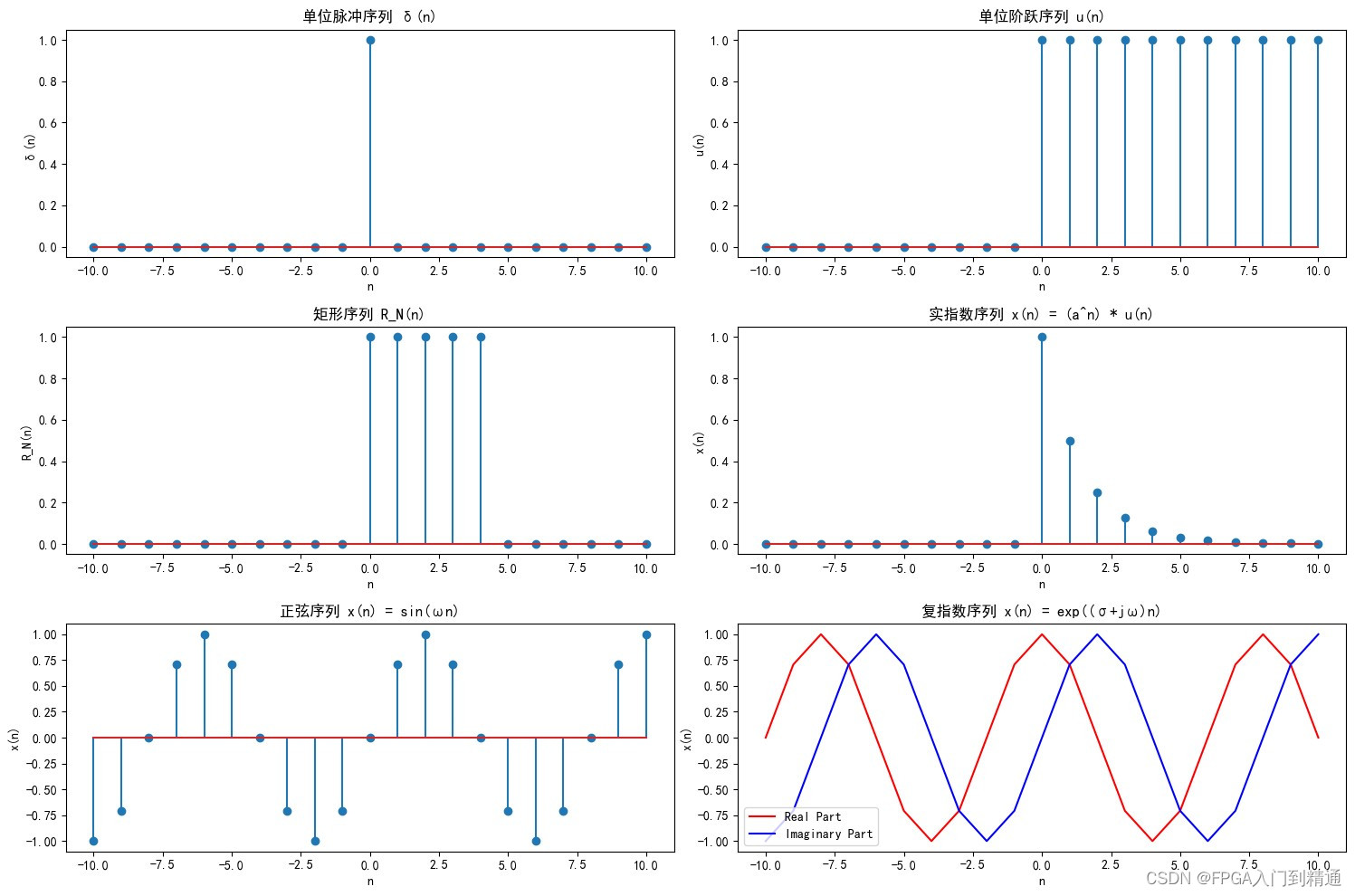
常用的典型序列如下:
单位脉冲序列:δ(n)
单位阶跃序列:u(n)
矩形序列:R_N(n)
实指数序列:x(n)=(a^n)*u(n)
正弦序列:x(n)=sin(ωn)
复指数序列:x(n)=exp((σ+jω)n)
五、时域中的信号运算
1、 信号的加法和减法
将两个信号在相同时间点上的取值相加或相减,得到一个新的信号。
例如,将一个正弦波信号和一个直流信号相加,就可以得到一个带有直流偏置的正弦波信号。
2、 信号的乘法
两个信号在对应时间点上的取值相乘,得到的乘积构成新的信号。
信号乘法常用于调制和解调等过程。
3、信号的延迟和提前
通过将信号在时间轴上进行平移,可以实现信号的延迟或提前。
例如,将一个音频信号延迟一段时间播放,就可以实现回声效果。
五、时域分析方法
1、波形观察
直接观察信号的波形图,了解信号的大致形状、幅度变化、周期等特征。
通过示波器等工具,我们可以直观地看到信号在时域中的表现。
2、过零检测
检测信号在哪些时间点上穿过零值。过零检测在很多领域都有应用,比如在数字通信中用于同步信号的提取。
3、相关分析
计算两个信号之间的相关程度。
相关分析可以用于信号的匹配、检测信号之间的相似性等。
六、时域与其他域的关系
数字信号处理除了时域,还有频域、时差域等其他域。
时域和频域之间通过傅里叶变换相互关联,傅里叶变换可以将时域信号转换到频域,反之亦然。
通过对信号在不同域的分析,我们能够从不同角度更全面地了解信号的特性。
七、实际应用中的时域考虑
在实际的 FPGA 开发中,时域的概念和分析方法具有重要的应用价值。
例如,在音频处理中,我们需要根据音频信号的时域特征进行滤波、降噪等操作,以提高音频质量;
在通信系统中,对时域信号的处理可以实现信号的调制、解调、同步等功能。
如果需要更多学习资料和源码,想要学习FPGA实战入门进阶,请阅读下面这篇文章:
FPGA入门真的难吗?少走弯路,少踩坑。