树链剖分——从入门到入坟

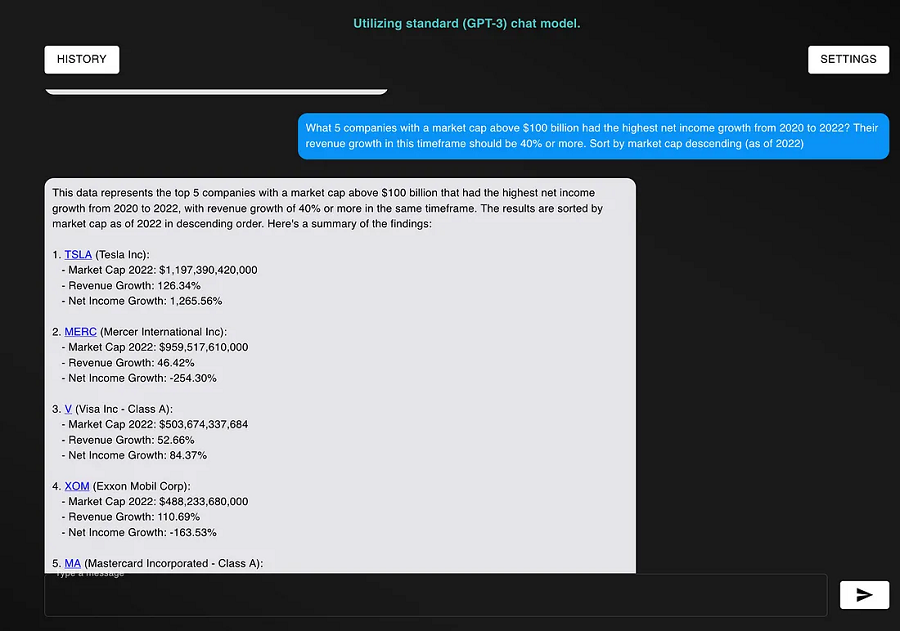
树链剖分的思想及能解决的问题

树链剖分用于将树分割成若干条链的形式，以维护树上路径的信息。

具体来说，将整棵树剖分为若干条链，使它组合成线性结构，然后用其他的数据结构维护信息。

树链剖分（树剖/链剖）有多种形式，如 重链剖分，长链剖分 和用于 Link/cut Tree 的剖分（有时被称作「实链剖分」），大多数情况下（没有特别说明时），「树链剖分」都指「重链剖分」。

重链剖分可以将树上的任意一条路径划分成不超过 $O(\log n)$ 条连续的链，每条链上的点深度互不相同（即是自底向上的一条链，链上所有点的 LCA 为链的一个端点）。

重链剖分还能保证划分出的每条链上的节点 DFS 序连续，因此可以方便地用一些维护序列的数据结构（如线段树）来维护树上路径的信息。

如：

修改 树上两点之间的路径上 所有点的值。
查询 树上两点之间的路径上 节点权值的 和/极值/其它（在序列上可以用数据结构维护，便于合并的信息）。

除了配合数据结构来维护树上路径信息，树剖还可以用来 $O(\log n)$ （且常数较小）地求 LCA。在某些题目中，还可以利用其性质来灵活地运用树剖。

重链剖分

我们给出一些定义：

定义 重子节点 表示其子节点中子树最大的子结点。如果有多个子树最大的子结点，取其一。如果没有子节点，就无重子节点。

定义 轻子节点 表示剩余的所有子结点。

从这个结点到重子节点的边为重边。

到其他轻子节点的边为轻边。

若干条首尾衔接的重边构成重链。

把落单的结点也当作重链，那么整棵树就被剖分成若干条重链。

如图：

在这里插入图片描述

实现

树剖的实现分两个 DFS 的过程。代码如下：

第一个 DFS 记录每个结点的父节点（fa）、深度（dep）、子树大小（sz）、重子节点（hs）。

// 第一遍DFS,子树大小，重儿子，父亲，深度
void dfs1(int u,int f)
{
	sz[u]=1;
	hs[u]=-1;
	fa[u]=f;
	dep[u]=dep[f]+1;
	for(auto v : e[u])
	{
		if(v==f) continue;
		dfs1(v,u);
		sz[u]+=sz[v];
		if(hs[u] == -1 || sz[hs[u]] < sz[v]) hs[u]=v;
	}
}

第二个 DFS 记录所在链的链顶（top，应初始化为结点本身）、重边优先遍历时的 DFS 序（id）、DFS 序对应的节点编号（）。

// 第二遍DFS,每一个点DFS序，重链上的链头的元素
void dfs2(int u,int t)
{
	l[u]=++tot;
	top[u]=t;
	id[tot]=u;
	if(hs[u]!=-1)
	{
		dfs2(hs[u],t);
	}
	for(auto v : e[u])
	{
		if(v!=hs[u]&&v!=fa[u])
		{
			dfs2(v,v);
		}
	}
	r[u]=tot;
}

以下为代码实现。

我们先给出一些定义：

$f a (x)$ 表示节点 $x$ 在树上的父亲。
$d e p (x)$ 表示节点 $x$ 在树上的深度。
$s i z (x)$ 表示节点 $x$ 的子树的节点个数。
$h s (x)$ 表示节点 $x$ 的 重儿子。
$t o p (x)$ 表示节点 $x$ 所在重链的顶部节点（深度最小）。
$df n (x)$ 表示节点 $x$ 的 DFS 序，也是其在树中的编号。

我们进行两遍 DFS 预处理出这些值，其中第一次 DFS 求出 $f a (x)$ ， $d e p (x)$ ， $s i z (x)$ ， $so n (x)$ ，第二次 DFS 求出 $t o p (x)$ ， $df n (x)$ ， $r nk (x)$ 。

重链剖分的性质

树上每个节点都属于且仅属于一条重链。

重链开头的结点不一定是重子节点（因为重边是对于每一个结点都有定义的）。

所有的重链将整棵树 完全剖分。

在剖分时 重边优先遍历，最后树的 DFS 序上，重链内的 DFS 序是连续的。按 DFN 排序后的序列即为剖分后的链。

一颗子树内的 DFS 序是连续的。

可以发现，当我们向下经过一条轻边时，所在子树的大小至少会除以二。

因此，对于树上的任意一条路径，把它拆分成从 LCA 分别向两边往下走，分别最多走 $O(\log n)$ 次，因此，树上的每条路径都可以被拆分成不超过 $O(\log n)$ 条重链。

常见应用

路径上维护

用树链剖分求树上两点路径权值和，伪代码如下：

$\begin{array}{l} \text{TREE-PATH-SUM }(u,v) \\ \begin{array}{ll} 1 & tot\gets 0 \\ 2 & \textbf{while }u.top\text{ is not }v.top \\ 3 & \qquad \textbf{if }u.top.deep< v.top.deep \\ 4 & \qquad \qquad \text{SWAP}(u, v) \\ 5 & \qquad tot\gets tot + \text{sum of values between }u\text{ and }u.top \\ 6 & \qquad u\gets u.top.father \\ 7 & tot\gets tot + \text{sum of values between }u\text{ and }v \\ 8 & \textbf{return } tot \end{array} \end{array}$

链上的 DFS 序是连续的，可以使用线段树、树状数组维护。

每次选择深度较大的链往上跳，直到两点在同一条链上。

同样的跳链结构适用于维护、统计路径上的其他信息。

子树维护

有时会要求，维护子树上的信息，譬如将以 $x$ 为根的子树的所有结点的权值增加 $v$ 。

在 DFS 搜索的时候，子树中的结点的 DFS 序是连续的。

每一个结点记录 bottom 表示所在子树连续区间末端的结点。

这样就把子树信息转化为连续的一段区间信息。

求最近公共祖先

P3379 【模板】最近公共祖先（LCA）

不断向上跳重链，当跳到同一条重链上时，深度较小的结点即为 LCA。

向上跳重链时需要先跳所在重链顶端深度较大的那个。

int LCA(int u,int v)
{
	while(top[u]!=top[v])
	{
		if(dep[top[u]] < dep[top[v]]) v=fa[top[v]];
		else u=fa[top[u]];
	}
	if(dep[u]<dep[v]) return u;
	else return v;
}

参考代码：

#include <bits/stdc++.h>
#define endl "\n"
#define int long long
using namespace std;

const int N = 5e5 + 3;

using i64 = long long;
int fa[N],hs[N],sz[N],id[N];
int top[N],dep[N],tot,l[N],r[N];
int n,m,s;
vector<int> e[N];
// 第一遍DFS,子树大小，重儿子，父亲，深度
void dfs1(int u,int f)
{
	sz[u]=1;
	hs[u]=-1;
	fa[u]=f;
	dep[u]=dep[f]+1;
	for(auto v : e[u])
	{
		if(v==f) continue;
		dfs1(v,u);
		sz[u]+=sz[v];
		if(hs[u] == -1 || sz[hs[u]] < sz[v]) hs[u]=v;
	}
}
// 第二遍DFS,每一个点DFS序，重链上的链头的元素
void dfs2(int u,int t)
{
	l[u]=++tot;
	top[u]=t;
	id[tot]=u;
	if(hs[u]!=-1)
	{
		dfs2(hs[u],t);
	}
	for(auto v : e[u])
	{
		if(v!=hs[u]&&v!=fa[u])
		{
			dfs2(v,v);
		}
	}
	r[u]=tot;
}
int LCA(int u,int v)
{
	while(top[u]!=top[v])
	{
		if(dep[top[u]] < dep[top[v]]) v=fa[top[v]];
		else u=fa[top[u]];
	}
	if(dep[u]<dep[v]) return u;
	else return v;
}
signed main()
{
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	cin>>n>>m>>s;
	for(int i=1;i<n;i++)
	{
		int u,v;
		cin>>u>>v;
		e[u].push_back(v);
		e[v].push_back(u);
	}
	dfs1(s,-1);
	dfs2(s,s);
	while(m--)
	{
		int a,b;
		cin>>a>>b;
		cout<<LCA(a,b)<<endl;
	}
}

例题

「ZJOI2008」树的统计

题目大意

对一棵有 $n$ 个节点，节点带权值的静态树，进行三种操作共 $q$ 次：

修改单个节点的权值；
查询 $u$ 到 $v$ 的路径上的最大权值；
查询 $u$ 到 $v$ 的路径上的权值之和。

保证 $1\le n\le 30000$ ， $0\le q\le 200000$ 。

解法

根据题面以及以上的性质，你的线段树需要维护三种操作：

单点修改；
区间查询最大值；
区间查询和。

单点修改很容易实现。

由于子树的 DFS 序连续（无论是否树剖都是如此），修改一个节点的子树只用修改这一段连续的 DFS 序区间。

问题是如何修改/查询两个节点之间的路径。

考虑我们是如何用 倍增法求解 LCA 的。首先我们 将两个节点提到同一高度，然后将两个节点一起向上跳。对于树链剖分也可以使用这样的思想。

在向上跳的过程中，如果当前节点在重链上，向上跳到重链顶端，如果当前节点不在重链上，向上跳一个节点。如此直到两节点相同。沿途更新/查询区间信息。

对于每个询问，最多经过 $O(\log n)$ 条重链，每条重链上线段树的复杂度为 $O(\log n)$ ，因此总时间复杂度为 $O(n\log n+q\log^2 n)$ 。实际上重链个数很难达到 $O(\log n)$ （可以用完全二叉树卡满），所以树剖在一般情况下常数较小。

给出一种代码实现：

#include<bits/stdc++.h>
#define endl "\n"
#define int long long
using namespace std;
const int N=2e5+3;
using i64 = long long;
int n,q;
int l[N],r[N],id[N],dep[N],hs[N],sz[N];
int fa[N],top[N],a[N],tot;
vector<int> e[N];
struct info
{
    int maxn,sums;
}tr[N*4];
void update(int p)
{
    tr[p].maxn=max(tr[2*p].maxn,tr[2*p+1].maxn);
    tr[p].sums=tr[2*p].sums+tr[2*p+1].sums;
}
info operator+(const info& a,const info& b)
{
    return (info){max(a.maxn,b.maxn),a.sums+b.sums};
}
void build(int p,int l,int r)
{
    if(l==r)
    {
        tr[p].maxn=a[id[l]],tr[p].sums=a[id[l]];
        return ;
    }
    int mid=(l+r)/2;
    build(2*p,l,mid);
    build(2*p+1,mid+1,r);
    update(p);
}
void modify(int p,int l,int r,int pos,int val)
{
    if(l==r)
    {
        tr[p].maxn=val,tr[p].sums=val;
        return ;
    }
    //cout<<p<<endl;
    int mid=(l+r)/2;
    if(pos<=mid) modify(2*p,l,mid,pos,val); 
    else modify(2*p+1,mid+1,r,pos,val);
    update(p);
}
info query(int p,int l,int r,int ql,int qr)
{
    //cout<<p<<endl;
    if(ql==l&&qr==r)
    {
        return tr[p];
    }
    int mid=(l+r)/2;
    if(qr<=mid) return query(2*p,l,mid,ql,qr);
    else if(ql>mid) return query(2*p+1,mid+1,r,ql,qr);
    else return query(2*p,l,mid,ql,mid)+query(2*p+1,mid+1,r,mid+1,qr);
}
void dfs1(int u,int f)
{
    sz[u]=1;
    hs[u]=-1;
    fa[u]=f;
    dep[u]=dep[f]+1;
    for(auto v: e[u])
    {
        if(v==f) continue;
        dfs1(v,u);
        sz[u]+=sz[v];
        if(hs[u] == -1 || sz[hs[u]] < sz[v]) hs[u]=v;
    }
    //cout<<u<<endl;
}
void dfs2(int u,int t)
{
    l[u]=++tot;
    id[tot]=u;
    top[u]=t;
    if(hs[u]!=-1) dfs2(hs[u],t);
    for(auto v : e[u])
    {
        if(v==hs[u]||v==fa[u]) continue;
        dfs2(v,v);
    }
    r[u]=tot;
}
info check(int u,int v)
{
    info ans={(int)-1e9,0};
    while(top[u]!=top[v])
    {
        if(dep[top[u]]>dep[top[v]])
        {
            ans=ans+query(1,1,n,l[top[u]],l[u]);
            u=fa[top[u]];
        }
        else
        {
            ans=ans+query(1,1,n,l[top[v]],l[v]);
            v=fa[top[v]];
        }
        //cout<<v<<endl;
    }
    //cout<<"111"<<endl;
    if(dep[u]>dep[v]) ans=ans+query(1,1,n,l[v],l[u]);
    else ans=ans+query(1,1,n,l[u],l[v]);
    return ans;
}
void solve()
{
    cin>>n;
    for(int i=1;i<n;i++)
    {
        int u,v;
        cin>>u>>v;
        e[u].push_back(v);
        e[v].push_back(u);
    }
    for(int i=1;i<=n;i++) cin>>a[i];
    cin>>q;
    dfs1(1,0);
    dfs2(1,1);
    build(1,1,n);
    //cout<<"ddddd"<<endl;
    while(q--)
    {
        string op;
        cin>>op;
        if(op[0]=='C')
        {
            int u,t;
            cin>>u>>t;
            modify(1,1,n,l[u],t);
        }
        else
        {
            int u,v;
            cin>>u>>v;
            info ans=check(u,v);
            if(op=="QMAX") cout<<ans.maxn<<endl;
            else cout<<ans.sums<<endl;
        }
    }

}
signed main()
{
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    int T;
    T=1;
    //cin>>T;
    while(T--)
     {
         solve();
     }
     return 0;
}

「SDOI2011」染色

题目大意

给定一棵 $n$ 个节点的无根树，共有 $m$ 个操作，操作分为两种：

将节点 $a$ 到节点 $b$ 的路径上的所有点（包括 $a$ 和 $b$ ）都染成颜色 $c$ 。
询问节点 $a$ 到节点 $b$ 的路径上的颜色段数量。

颜色段的定义是极长的连续相同颜色被认为是一段。例如 112221 由三段组成：11、222、1。

对于 $100\%$ 的数据， $\leq n, m \leq 10^5$ ， $\leq w_i, c \leq 10^9$ ， $\leq a, b, u, v \leq n$ ， $o p$ 一定为 C 或 Q，保证给出的图是一棵树。

解法

根据题面以及以上的性质，你的线段树需要维护三种操作：

左边颜色；
右边颜色；
颜色段数量。

代码：

#include<bits/stdc++.h>
#define endl "\n"
#define int long long
using namespace std;
const int N=2e5+3;
using i64 = long long;
int n,q;
int l[N],r[N],id[N],dep[N],hs[N],sz[N];
int fa[N],top[N],a[N],tot;
vector<int> e[N];
struct info
{
   int lc,rc,seg;
};
struct node
{
    info val;
    int tag;
}tr[N*4];
info operator+(const info& a,const info& b)
{
    info ans={0,0,0};
    ans={a.lc,b.rc,a.seg+b.seg-(a.rc==b.lc)};
    return ans;
}
void update(int p)
{
    tr[p].val=tr[2*p].val+tr[2*p+1].val;
}
void settag(int p,int t)
{
    tr[p].tag=t;
    tr[p].val={t,t,1};
}
void pushdown(int p)
{
    if(tr[p].tag!=0)
    {
        int t=tr[p].tag;
        settag(2*p,t);
        settag(2*p+1,t);
        tr[p].tag=0;
    }
}
void build(int p,int l,int r)
{
    if(l==r)
    {
        tr[p].val={a[id[l]],a[id[l]],1};
        tr[p].tag=0;
        return ;
    }
    int mid=(l+r)/2;
    build(2*p,l,mid);
    build(2*p+1,mid+1,r);
    update(p);
}
void modify(int p,int l,int r,int ql,int qr,int tag)
{
    if(ql==l&&qr==r)
    {
        settag(p,tag);
        return ;
    }
    pushdown(p);
    int mid=(l+r)/2;
    if(qr<=mid) modify(2*p,l,mid,ql,qr,tag); 
    else if(ql>mid) modify(2*p+1,mid+1,r,ql,qr,tag);
    else{
        modify(2*p,l,mid,ql,mid,tag);
        modify(2*p+1,mid+1,r,mid+1,qr,tag);
    }
    update(p);
}
info query(int p,int l,int r,int ql,int qr)
{
    //cout<<p<<endl;
    if(ql==l&&qr==r)
    {
        return tr[p].val;
    }
    pushdown(p);
    int mid=(l+r)/2;
    if(qr<=mid) return query(2*p,l,mid,ql,qr);
    else if(ql>mid) return query(2*p+1,mid+1,r,ql,qr);
    else return query(2*p,l,mid,ql,mid)+query(2*p+1,mid+1,r,mid+1,qr);
}
int query(int u,int v)
{
    info ansu={0,0,0},ansv={0,0,0};
    while(top[u]!=top[v])
    {
        if(dep[top[u]]>dep[top[v]])
        {
            ansu=query(1,1,n,l[top[u]],l[u])+ansu;
            u=fa[top[u]];
        }
        else
        {
            ansv=query(1,1,n,l[top[v]],l[v])+ansv;
            v=fa[top[v]];
        }
    }
    if(dep[u]>dep[v]) ansu=query(1,1,n,l[v],l[u])+ansu;
    else ansv=query(1,1,n,l[u],l[v])+ansv;
    int res=ansu.seg+ansv.seg-(ansu.lc==ansv.lc);
    return res;
}
void modify(int u,int v,int w)
{
    while(top[u]!=top[v])
    {
        if(dep[top[u]]>dep[top[v]])
        {
            modify(1,1,n,l[top[u]],l[u],w);
            u=fa[top[u]];
        }
        else
        {
            modify(1,1,n,l[top[v]],l[v],w);
            v=fa[top[v]];
        }
    }
    if(dep[u]>dep[v]) modify(1,1,n,l[v],l[u],w);
    else modify(1,1,n,l[u],l[v],w);
}
void dfs1(int u,int f)
{
    sz[u]=1;
    hs[u]=-1;
    fa[u]=f;
    dep[u]=dep[f]+1;
    for(auto v: e[u])
    {
        if(v==f) continue;
        dfs1(v,u);
        sz[u]+=sz[v];
        if(hs[u] == -1 || sz[hs[u]] < sz[v]) hs[u]=v;
    }
    //cout<<u<<endl;
}
void dfs2(int u,int t)
{
    l[u]=++tot;
    id[tot]=u;
    top[u]=t;
    if(hs[u]!=-1) dfs2(hs[u],t);
    for(auto v : e[u])
    {
        if(v==hs[u]||v==fa[u]) continue;
        dfs2(v,v);
    }
    r[u]=tot;
}
void solve()
{
    cin>>n>>q;
    for(int i=1;i<=n;i++) cin>>a[i];
    for(int i=1;i<n;i++)
    {
        int u,v;
        cin>>u>>v;
        e[u].push_back(v);
        e[v].push_back(u);
    }
    dfs1(1,0);
    dfs2(1,1);
    build(1,1,n);
    //cout<<"ddddd"<<endl;
    while(q--)
    {
        string op;
        cin>>op;
        if(op[0]=='C')
        {
            int u,v,w;
            cin>>u>>v>>w;
            modify(u,v,w);
        }
        else
        {
            int u,v;
            cin>>u>>v;
            int ans=query(u,v);
            cout<<ans<<endl;
        }
    }

}
signed main()
{
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    int T;
    T=1;
    //cin>>T;
    while(T--)
     {
         solve();
     }
     return 0;
}