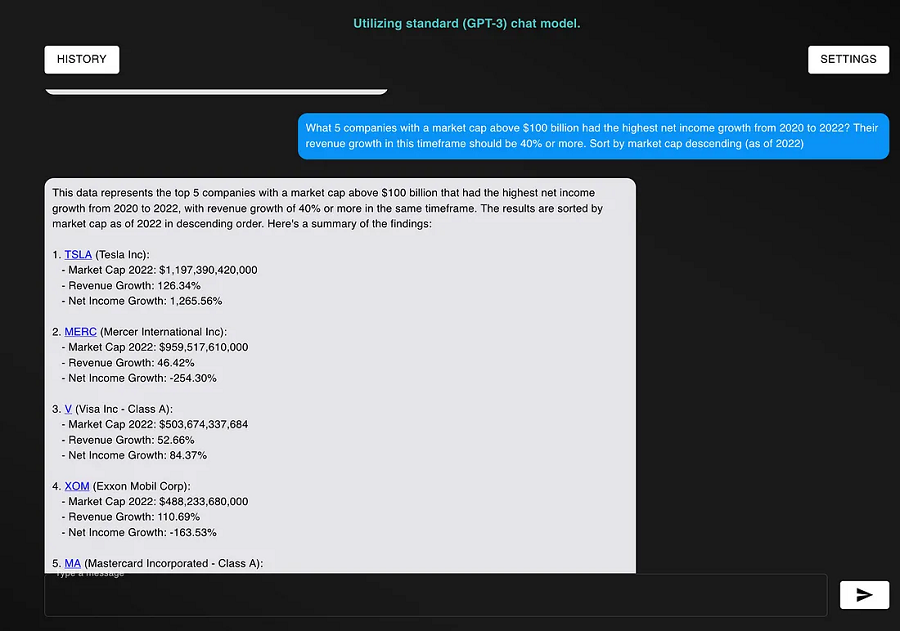
不平衡分类阈值移动的简单介绍

分类预测模型通常涉及预测类别标签。

尽管如此，许多机器学习算法能够预测类别成员的概率或得分，并且必须对其进行解释，然后才能将其映射到明确的类别标签。这是通过使用阈值（例如 0.5）来实现的，其中所有等于或大于阈值的值都映射到一个类，而所有其他值都映射到另一个类。

对于存在严重类别不平衡的分类问题，默认阈值可能会导致性能不佳。因此，提高分类器性能（用于预测不平衡分类问题的概率）的一种简单直接的方法是调整用于将概率映射到类别标签的阈值。

在某些情况下，例如使用 ROC 曲线和准确率-召回率曲线时，可以直接计算分类器的最佳或最优阈值。在其他情况下，可以使用网格搜索来调整阈值并找到最优值。

在本教程中，您将了解如何在将概率转换为不平衡分类的清晰类标签时调整最佳阈值。

完成本教程后，您将了解：

• 将概率解释为类标签的默认阈值为 0.5，调整此超参数称为阈值移动。
• 如何直接计算ROC曲线和准确率-召回率曲线的最佳阈值。
• 如何手动搜索所选模型和模型评估指标的阈值。

教程概述

本教程分为五个部分，分别是：

1. 将概率转换为类别标签
2. 不平衡分类的阈值移动
3. ROC 曲线的最佳阈值
4. 准确率-召回率曲线的最佳阈值
5. 最佳阈值调整

将概率转换为类别标签

许多机器学习算法能够预测类别成员的概率或得分。

这通常很有用，因为它可以衡量预测的确定性或不确定性。它还提供了比仅仅预测可解释的类标签更多的粒度。

一些分类任务需要明确的类别标签预测。这意味着，即使预测了类别成员的概率或得分，也必须将其转换为明确的类别标签。

将预测概率或得分转换为类标签的决定由称为“决策阈值”、“判别阈值”或简称为“阈值”的参数控制。对于 0 或 1 之间的归一化预测概率或得分，阈值的默认值为 0.5。

例如，在类标签为 0 和 1、预测概率为归一化且阈值为 0.5 的二元分类问题中，小于阈值 0.5 的值分配给类 0，大于或等于 0.5 的值分配给类 1。

• 预测值 < 0.5 = 0 类
• 预测 >= 0.5 = 1 类

问题在于默认阈值可能无法代表预测概率的最佳解释。

出现这种情况可能有多种原因，例如：

• 预测概率未经校准，例如由 SVM 或决策树预测的概率。
• 用于训练模型的指标与用于评估最终模型的指标不同。
• 阶级分布严重不平衡。
• 一种错误分类的成本比另一种错误分类的成本更重要。

更糟糕的是，这些原因中的部分或全部可能同时发生，例如在不平衡分类问题上使用具有未校准预测概率的神经网络模型。

因此，在解释模型的预测时经常需要改变默认决策阈值。

…几乎所有分类器都会通过对分数应用阈值来生成正或负预测。此阈值的选择将对正负误差的权衡产生影响。

— 第 53 页，从不平衡数据集学习，2018 年。

不平衡分类的阈值移动

有许多技术可用于解决不平衡分类问题，例如重新采样训练数据集和开发定制版本的机器学习算法。

然而，处理严重类别不平衡问题最简单的方法可能是改变决策阈值。尽管这种方法简单且非常有效，但实践者和研究学者往往忽视了这种方法，正如 Foster Provost 在 2000 年题为“从不平衡数据集进行机器学习”的文章中所指出的那样。

底线是，在研究不平衡数据问题时，使用标准机器学习算法产生的分类器而不调整输出阈值很可能是一个严重的错误。

—从不平衡数据集进行机器学习 101，2000年。

选择默认决策阈值的替代方案的原因有很多。

例如，虽然您需要模型中的明确类别标签，但您可以使用ROC 曲线来分析模型的预测概率，并使用 ROC AUC 分数来比较和选择模型。如何选择 ROC 曲线上的阈值，以便在真阳性率和假阳性率之间取得最佳平衡？

或者，您可以使用精确召回率曲线来分析模型的预测概率，使用精确召回率 AUC 来比较和选择模型，并要求清晰的类标签作为预测。如何选择精确召回率曲线上的阈值，以实现精确度和召回率之间的最佳平衡？

您可以使用基于概率的指标来训练、评估和比较对数损失（[交叉熵]）等模型，但需要预测清晰的类标签。如何更普遍地从预测概率中选择最佳阈值？

最后，您可能拥有与假阳性和假阴性错误分类相关的不同成本，即所谓的成本矩阵，但希望使用和评估成本不敏感的模型，然后使用成本敏感的度量来评估它们的预测。如何使用成本矩阵选择一个阈值来找到预测的最佳权衡？

在没有已知成本矩阵的情况下训练成本敏感分类器的流行方法是，在对新数据进行预测时，重点修改分类输出。这通常是通过对正类设置阈值来实现的，低于该阈值的预测为负类。使用验证集优化此阈值的值，从而可以从训练数据中学习成本矩阵。

— 第 67 页，从不平衡数据集中学习，2018 年。

这些问题的答案是搜索一系列阈值以找到最佳阈值。在某些情况下，最佳阈值可以直接计算出来。

为了适应分类问题的更广泛要求而调整或改变决策阈值通常被称为“阈值移动”、“阈值调整”或简称为“阈值处理”。

有人指出，尝试其他方法（例如抽样）而不通过简单地设置阈值进行尝试可能会产生误导。阈值移动方法使用原始训练集来训练[模型]，然后移动决策阈值，以便少数类示例更容易被正确预测。

— 第 72 页，《不平衡学习：基础、算法和应用》，2013 年。

该过程首先涉及在训练数据集上拟合模型，然后在测试数据集上进行预测。预测的形式为归一化概率或分数，这些分数会转换为归一化概率。然后尝试不同的阈值，并使用所选的评估指标评估生成的清晰标签。然后在对未来新数据进行预测时，为模型采用达到最佳评估指标的阈值。

我们可以在下面总结这个过程。

• 1.在训练数据集上拟合模型。

• 2. 预测测试数据集上的概率。
• 3. 对于阈值中的每个阈值：
  • 3a. 使用阈值将概率转换为类标签。
  • 3b.评估类别标签。
  • 3c. 如果分数高于最佳分数。
    • 3ci. 采用阈值。
  • 4. 对新数据进行类别预测时使用采用的阈值。

虽然很简单，但根据您的情况，有几种不同的方法可以实现阈值移动。我们将在以下部分中介绍一些最常见的示例。

ROC 曲线的最佳阈值

ROC 曲线是一种诊断图，用于评估模型在测试数据集上做出的一组概率预测。

使用一组不同的阈值来解释正（少数）类预测的真阳性率和假阳性率，并将分数绘制在一条不断增加的阈值线上以创建曲线。

x 轴表示假阳性率，y 轴表示真阳性率，该图称为接收者操作特征曲线，或 ROC 曲线。图上从左下角到右上的对角线表示无技能分类器的“曲线*”*（在所有情况下都预测多数类），图左上角的点表示具有完美技能的模型。

该曲线有助于理解不同阈值的真阳性率和假阳性率之间的权衡。ROC 曲线下的面积，即所谓的 ROC AUC，提供了一个数字来总结模型在 ROC 曲线方面的表现，其值介于 0.5（无技能）和 1.0（完美技能）之间。

ROC 曲线是一种有用的诊断工具，可以用于了解不同阈值的权衡，而 ROC AUC 则提供了一个有用的数字，可用于根据模型的一般能力对其进行比较。

如果在这样的分析下，模型需要清晰的类别标签，那么就需要一个最佳阈值。这将是曲线上最接近图左上角的阈值。

值得庆幸的是，有原则性的方法可以找到这一点。

首先，让我们拟合一个模型并计算ROC曲线。

我们可以使用make_classification() 函数创建一个包含 10,000 个示例（行）的合成二元分类问题，其中 99％ 属于多数类，1％ 属于少数类。

...
# generate dataset
X, y = make_classification(n_samples=10000, n_features=2, n_redundant=0,
	n_clusters_per_class=1, weights=[0.99], flip_y=0, random_state=4)

然后，我们可以使用train_test_split() 函数分割数据集，一半作为训练集，一半作为测试集。

...
# split into train/test sets
trainX, testX, trainy, testy = train_test_split(X, y, test_size=0.5, random_state=2, stratify=y)

然后我们可以拟合一个LogisticRegression 模型并使用它对测试集进行概率预测，并仅保留少数类的概率预测。

...
# fit a model
model = LogisticRegression(solver='lbfgs')
model.fit(trainX, trainy)
# predict probabilities
lr_probs = model.predict_proba(testX)
# keep probabilities for the positive outcome only
lr_probs = lr_probs[:, 1]

然后，我们可以使用roc_auc_score() 函数使用一组阈值计算预测的真阳性率和假阳性率，然后可以使用这些阈值创建 ROC 曲线图。

...
# calculate scores
lr_auc = roc_auc_score(testy, lr_probs)

我们可以把所有这些结合在一起，定义数据集，拟合模型，并创建 ROC 曲线图。完整的示例如下所示。

# roc curve for logistic regression model
from sklearn.datasets import make_classification
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import roc_curve
from matplotlib import pyplot
# generate dataset
X, y = make_classification(n_samples=10000, n_features=2, n_redundant=0,
	n_clusters_per_class=1, weights=[0.99], flip_y=0, random_state=4)
# split into train/test sets
trainX, testX, trainy, testy = train_test_split(X, y, test_size=0.5, random_state=2, stratify=y)
# fit a model
model = LogisticRegression(solver='lbfgs')
model.fit(trainX, trainy)
# predict probabilities
yhat = model.predict_proba(testX)
# keep probabilities for the positive outcome only
yhat = yhat[:, 1]
# calculate roc curves
fpr, tpr, thresholds = roc_curve(testy, yhat)
# plot the roc curve for the model
pyplot.plot([0,1], [0,1], linestyle='--', label='No Skill')
pyplot.plot(fpr, tpr, marker='.', label='Logistic')
# axis labels
pyplot.xlabel('False Positive Rate')
pyplot.ylabel('True Positive Rate')
pyplot.legend()
# show the plot
pyplot.show()

运行该示例会在训练数据集上拟合逻辑回归模型，然后使用测试集上的一系列阈值对其进行评估，从而创建 ROC 曲线

我们可以看到，在图的左上角附近有许多点或阈值。

哪一个阈值是最佳的？

不平衡分类的逻辑回归模型的 ROC 曲线图

我们可以通过多种方式找到在假阳性率和真阳性率之间达到最佳平衡的阈值。

首先，真阳性率称为敏感性。假阳性率的倒数称为特异性。

• 灵敏度 = TruePositive / (TruePositive + FalseNegative)
• 特异性 = 真阴性 / （假阳性 + 真阴性）

在哪里：

• 敏感度 = 真阳性率
• 特异性 = 1 – 假阳性率

几何平均值或 G-Mean 是不平衡分类的度量，如果进行优化，将在敏感性和特异性之间寻求平衡。

• G-均值 = sqrt（敏感度 * 特异性）

一种方法是使用调用roc_auc_score()返回的每个阈值来测试模型，并选择具有最大 G-Mean 值的阈值。

鉴于我们在计算 ROC 曲线时已经计算了敏感性 (TPR) 和特异性的补充，我们可以直接计算每个阈值的 G-Mean。

...
# calculate the g-mean for each threshold
gmeans = sqrt(tpr * (1-fpr))

一旦计算出来，我们就可以找到最大 G 均值分数的指数，并使用该指数确定使用哪个阈值。

...
# locate the index of the largest g-mean
ix = argmax(gmeans)
print('Best Threshold=%f, G-Mean=%.3f' % (thresholds[ix], gmeans[ix]))

我们还可以重新绘制 ROC 曲线并突出显示这一点。

完整的示例如下。

# roc curve for logistic regression model with optimal threshold
from numpy import sqrt
from numpy import argmax
from sklearn.datasets import make_classification
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import roc_curve
from matplotlib import pyplot
# generate dataset
X, y = make_classification(n_samples=10000, n_features=2, n_redundant=0,
	n_clusters_per_class=1, weights=[0.99], flip_y=0, random_state=4)
# split into train/test sets
trainX, testX, trainy, testy = train_test_split(X, y, test_size=0.5, random_state=2, stratify=y)
# fit a model
model = LogisticRegression(solver='lbfgs')
model.fit(trainX, trainy)
# predict probabilities
yhat = model.predict_proba(testX)
# keep probabilities for the positive outcome only
yhat = yhat[:, 1]
# calculate roc curves
fpr, tpr, thresholds = roc_curve(testy, yhat)
# calculate the g-mean for each threshold
gmeans = sqrt(tpr * (1-fpr))
# locate the index of the largest g-mean
ix = argmax(gmeans)
print('Best Threshold=%f, G-Mean=%.3f' % (thresholds[ix], gmeans[ix]))
# plot the roc curve for the model
pyplot.plot([0,1], [0,1], linestyle='--', label='No Skill')
pyplot.plot(fpr, tpr, marker='.', label='Logistic')
pyplot.scatter(fpr[ix], tpr[ix], marker='o', color='black', label='Best')
# axis labels
pyplot.xlabel('False Positive Rate')
pyplot.ylabel('True Positive Rate')
pyplot.legend()
# show the plot
pyplot.show()

首先运行示例找到最佳阈值并报告该阈值和 G-Mean 分数。

注意：由于算法或评估程序的随机性，或数值精度的差异，您的结果可能会有所不同。考虑运行示例几次并比较平均结果。

在这种情况下，我们可以看到最佳阈值约为 0.016153。

Best Threshold=0.016153, G-Mean=0.933

然后使用阈值来定位真阳性率和假阳性率，然后在 ROC 曲线上绘制该点。

我们可以看到最佳阈值的点是一个大黑点，它似乎最接近图的左上角。

具有最佳阈值的不平衡分类逻辑回归模型的 ROC 曲线图

事实证明，有一种更快捷的方法可以获得相同的结果，称为Youden’s J 统计量。

统计量计算如下：

• J = 敏感性 + 特异性 – 1

假设我们有敏感性（TPR）和特异性（FPR）的补充，我们可以按如下方式计算：

• J = 敏感度 + (1 - 假阳性率) - 1

我们可以重申如下：

• J = 真阳性率 – 假阳性率

然后我们可以选择具有最大 J 统计值的阈值。例如：

...
# calculate roc curves
fpr, tpr, thresholds = roc_curve(testy, yhat)
# get the best threshold
J = tpr - fpr
ix = argmax(J)
best_thresh = thresholds[ix]
print('Best Threshold=%f' % (best_thresh))

插入后，完整的示例如下所示。

# roc curve for logistic regression model with optimal threshold
from numpy import argmax
from sklearn.datasets import make_classification
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import roc_curve
# generate dataset
X, y = make_classification(n_samples=10000, n_features=2, n_redundant=0,
	n_clusters_per_class=1, weights=[0.99], flip_y=0, random_state=4)
# split into train/test sets
trainX, testX, trainy, testy = train_test_split(X, y, test_size=0.5, random_state=2, stratify=y)
# fit a model
model = LogisticRegression(solver='lbfgs')
model.fit(trainX, trainy)
# predict probabilities
yhat = model.predict_proba(testX)
# keep probabilities for the positive outcome only
yhat = yhat[:, 1]
# calculate roc curves
fpr, tpr, thresholds = roc_curve(testy, yhat)
# get the best threshold
J = tpr - fpr
ix = argmax(J)
best_thresh = thresholds[ix]
print('Best Threshold=%f' % (best_thresh))

我们可以看到，这种更简单的方法直接计算最佳统计数据。

Best Threshold=0.016153

准确率-召回率曲线的最佳阈值

与 ROC 曲线不同，精确召回率曲线仅关注分类器在正类（少数类）上的表现。

准确率是真阳性数量除以真阳性和假阳性之和的比率。它描述了模型预测阳性类别的能力。召回率是真阳性数量除以真阳性和假阴性之和的比率。召回率与敏感度相同。

精确度-召回率曲线的计算方法是，为一组阈值的概率预测创建清晰的类别标签，并计算每个阈值的精确度和召回率。按阈值升序创建线图，召回率在 x 轴上，精确度在 y 轴上。

无技能模型用一条水平线表示，其精度是数据集中正例的比例（例如 TP /（TP + TN）），或在我们的合成数据集上为 0.01。完美技能分类器具有完整的精度和召回率，右上角有一个点。

我们可以使用上一节中的相同模型和数据集，并使用精确度-召回率曲线评估逻辑回归模型的概率预测。precision_recall_curve() 函数可用于计算曲线，返回每个阈值的精确度和召回率分数以及使用的阈值。

...
# calculate pr-curve
precision, recall, thresholds = precision_recall_curve(testy, yhat)

综合以上几点，下面列出了计算不平衡分类问题逻辑回归的精确召回率曲线的完整示例。

# pr curve for logistic regression model
from sklearn.datasets import make_classification
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import precision_recall_curve
from matplotlib import pyplot
# generate dataset
X, y = make_classification(n_samples=10000, n_features=2, n_redundant=0,
	n_clusters_per_class=1, weights=[0.99], flip_y=0, random_state=4)
# split into train/test sets
trainX, testX, trainy, testy = train_test_split(X, y, test_size=0.5, random_state=2, stratify=y)
# fit a model
model = LogisticRegression(solver='lbfgs')
model.fit(trainX, trainy)
# predict probabilities
yhat = model.predict_proba(testX)
# keep probabilities for the positive outcome only
yhat = yhat[:, 1]
# calculate pr-curve
precision, recall, thresholds = precision_recall_curve(testy, yhat)
# plot the roc curve for the model
no_skill = len(testy[testy==1]) / len(testy)
pyplot.plot([0,1], [no_skill,no_skill], linestyle='--', label='No Skill')
pyplot.plot(recall, precision, marker='.', label='Logistic')
# axis labels
pyplot.xlabel('Recall')
pyplot.ylabel('Precision')
pyplot.legend()
# show the plot
pyplot.show()

运行该示例将计算每个阈值的精确度和召回率，并创建一个精确度-召回率图，表明该模型在该数据集的一系列阈值上具有一定的技能。

如果我们需要该模型提供清晰的类别标签，哪个阈值可以获得最佳结果？

不平衡分类的逻辑回归模型的精确率-召回率曲线图

如果我们对导致精确度和召回率最佳平衡的阈值感兴趣，那么这与优化总结两个度量的调和平均值的 F 度量相同。

• F 测量值 = (2 * 准确率 * 召回率) / (准确率 + 召回率)

与上一节一样，找到最佳阈值的简单方法是计算每个阈值的 F 度量。我们可以通过将精度和召回率度量直接转换为 F 度量来实现相同的效果；例如：

...
# convert to f score
fscore = (2 * precision * recall) / (precision + recall)
# locate the index of the largest f score
ix = argmax(fscore)
print('Best Threshold=%f, F-Score=%.3f' % (thresholds[ix], fscore[ix]))

然后我们可以绘制精确度-召回率曲线上的点。

完整的示例如下。

# optimal threshold for precision-recall curve with logistic regression model
from numpy import argmax
from sklearn.datasets import make_classification
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import precision_recall_curve
from matplotlib import pyplot
# generate dataset
X, y = make_classification(n_samples=10000, n_features=2, n_redundant=0,
	n_clusters_per_class=1, weights=[0.99], flip_y=0, random_state=4)
# split into train/test sets
trainX, testX, trainy, testy = train_test_split(X, y, test_size=0.5, random_state=2, stratify=y)
# fit a model
model = LogisticRegression(solver='lbfgs')
model.fit(trainX, trainy)
# predict probabilities
yhat = model.predict_proba(testX)
# keep probabilities for the positive outcome only
yhat = yhat[:, 1]
# calculate roc curves
precision, recall, thresholds = precision_recall_curve(testy, yhat)
# convert to f score
fscore = (2 * precision * recall) / (precision + recall)
# locate the index of the largest f score
ix = argmax(fscore)
print('Best Threshold=%f, F-Score=%.3f' % (thresholds[ix], fscore[ix]))
# plot the roc curve for the model
no_skill = len(testy[testy==1]) / len(testy)
pyplot.plot([0,1], [no_skill,no_skill], linestyle='--', label='No Skill')
pyplot.plot(recall, precision, marker='.', label='Logistic')
pyplot.scatter(recall[ix], precision[ix], marker='o', color='black', label='Best')
# axis labels
pyplot.xlabel('Recall')
pyplot.ylabel('Precision')
pyplot.legend()
# show the plot
pyplot.show()

运行示例首先计算每个阈值的 F 度量，然后找到具有最大值的分数和阈值。

注意：由于算法或评估程序的随机性，或数值精度的差异，您的结果可能会有所不同。考虑运行示例几次并比较平均结果。

Best Threshold=0.256036, F-Score=0.756

在这种情况下，我们可以看到最佳 F 度量为 0.756，阈值约为 0.25。

绘制了精确度-召回率曲线，这次用较大的黑点绘制了具有最佳 F 度量的阈值。

然后可以使用该阈值来在未来进行概率预测，并将其从概率转换为明确的类标签。

具有最佳阈值的逻辑回归模型的精确度-召回率曲线图

最佳阈值调整

有时，我们只是有一个模型，我们希望直接知道最佳阈值。

在这种情况下，我们可以定义一组阈值，然后评估每个阈值下的预测概率，以便找到并选择最佳阈值。

我们可以用一个实际例子来证明这一点。

首先，我们可以对我们的综合分类问题拟合一个逻辑回归模型，然后预测类标签并使用 F 度量（即准确率和召回率的调和平均值）对其进行评估。

在解释逻辑回归模型预测的概率时，这将使用默认阈值 0.5。

完整的示例如下。

# logistic regression for imbalanced classification
from sklearn.datasets import make_classification
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import f1_score
# generate dataset
X, y = make_classification(n_samples=10000, n_features=2, n_redundant=0,
	n_clusters_per_class=1, weights=[0.99], flip_y=0, random_state=4)
# split into train/test sets
trainX, testX, trainy, testy = train_test_split(X, y, test_size=0.5, random_state=2, stratify=y)
# fit a model
model = LogisticRegression(solver='lbfgs')
model.fit(trainX, trainy)
# predict labels
yhat = model.predict(testX)
# evaluate the model
score = f1_score(testy, yhat)
print('F-Score: %.5f' % score)

注意：由于算法或评估程序的随机性，或数值精度的差异，您的结果可能会有所不同。考虑运行示例几次并比较平均结果。

运行示例，我们可以看到该模型在测试数据集上实现了约 0.70 的 F 测量值。

F-Score: 0.70130

现在我们可以在相同的数据集上使用相同的模型，而不是直接预测类标签，而是可以预测概率。

...
# predict probabilities
yhat = model.predict_proba(testX)

我们只需要正类的概率。

...
# keep probabilities for the positive outcome only
probs = yhat[:, 1]

接下来，我们可以定义一组阈值来评估概率。在本例中，我们将以 0.001 的步长测试 0.0 到 1.0 之间的所有阈值，也就是说，我们将测试 0.0、0.001、0.002、0.003 等等，直到 0.999。

...
# define thresholds
thresholds = arange(0, 1, 0.001)

接下来，我们需要一种使用单一阈值来解释预测概率的方法来。

这可以通过将所有等于或大于阈值的值映射到 1 并将所有小于阈值的值映射到 0 来实现。我们将定义一个*to_labels()*函数来执行此操作，该函数将概率和阈值作为参数并返回 {0, 1} 中的整数数组。

# apply threshold to positive probabilities to create labels
def to_labels(pos_probs, threshold):
	return (pos_probs >= threshold).astype('int')

*然后，我们可以对每个阈值调用此函数，并使用f1_score()*评估生成的标签。

我们可以在一行中完成此操作，如下所示：

...
# evaluate each threshold
scores = [f1_score(testy, to_labels(probs, t)) for t in thresholds]

我们现在有一个分数数组，用于评估阈值数组中的每个阈值。

我们现在需要做的就是找到具有最大分数（最佳 F 测量）的数组索引，然后我们将得到最佳阈值及其评估。

...
# get best threshold
ix = argmax(scores)
print('Threshold=%.3f, F-Score=%.5f' % (thresholds[ix], scores[ix]))

综合以上所有，下面列出了在合成的不平衡分类数据集上调整逻辑回归模型阈值的完整示例。

# search thresholds for imbalanced classification
from numpy import arange
from numpy import argmax
from sklearn.datasets import make_classification
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import f1_score

# apply threshold to positive probabilities to create labels
def to_labels(pos_probs, threshold):
	return (pos_probs >= threshold).astype('int')

# generate dataset
X, y = make_classification(n_samples=10000, n_features=2, n_redundant=0,
	n_clusters_per_class=1, weights=[0.99], flip_y=0, random_state=4)
# split into train/test sets
trainX, testX, trainy, testy = train_test_split(X, y, test_size=0.5, random_state=2, stratify=y)
# fit a model
model = LogisticRegression(solver='lbfgs')
model.fit(trainX, trainy)
# predict probabilities
yhat = model.predict_proba(testX)
# keep probabilities for the positive outcome only
probs = yhat[:, 1]
# define thresholds
thresholds = arange(0, 1, 0.001)
# evaluate each threshold
scores = [f1_score(testy, to_labels(probs, t)) for t in thresholds]
# get best threshold
ix = argmax(scores)
print('Threshold=%.3f, F-Score=%.5f' % (thresholds[ix], scores[ix]))

运行示例报告最佳阈值为 0.251（相比默认值 0.5），实现的 F 测量值约为 0.75（相比默认值 0.70）。

注意：由于算法或评估程序的随机性，或数值精度的差异，您的结果可能会有所不同。考虑运行示例几次并比较平均结果。

您可以将此示例作为模板来调整您自己的问题的阈值，从而允许您替换您想要评估的自己的模型、度量甚至阈值分辨率。

Threshold=0.251, F-Score=0.75556