c语言自定义类型--枚举、联合 #枚举类型的定义 #枚举的优点 #枚举的使用 #联合类型的定义 #联合的特点 #联合大小的计算

文章目录

前言

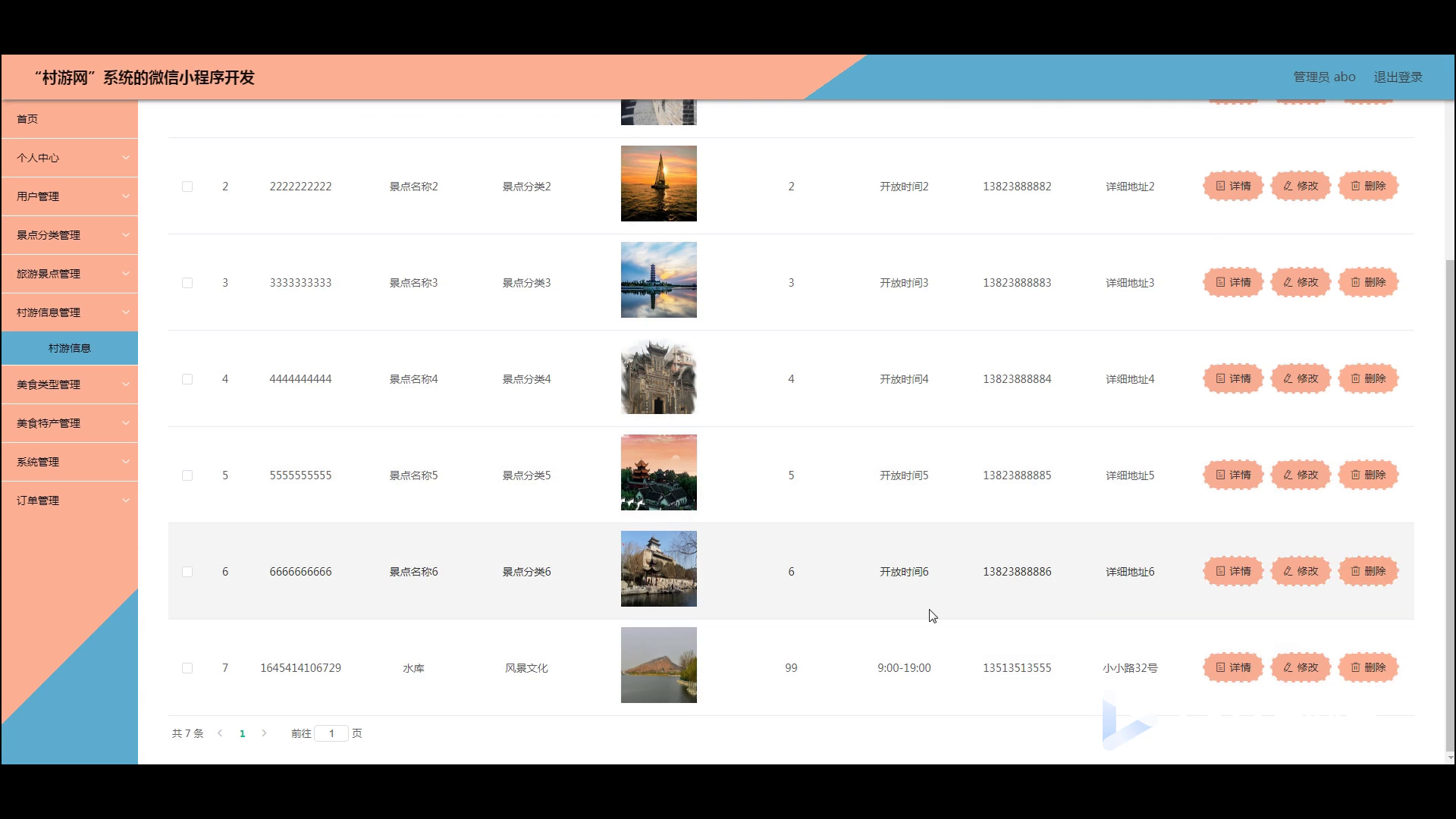
一、枚举

(一)、枚举类型的定义

(二)、枚举的优点

(三)、枚举的使用

二、联合

(一)、联合类型的定义

(二)、联合的特点

(三)、联合大小的计算

总结

前言

路漫漫其修远兮，吾将上下而求索。

枚举、联合跟结构体很像，想要细致地了解结构的相关知识可以戳此链接：http://t.csdnimg.cn/1mymb

一、枚举

在正文开始之前，我们先从定义下手；怎样理解枚举呢？

枚举，顾名思义，看见枚，我们不难想到一枚一枚的量词，连在一起读枚举就有种一一列举的感觉在里面；

例如：星期可以枚举为：星期一、星期二、星期三、星期四、星期五、星期六、星期天。其中这些别列举出来的便叫作枚举常量；

注：这些取值只能是有限的几种且可以被一一列举出来，那么此时便可以将这些数据以枚举的形式列举出来；

枚举关键字：enum

我是这样理解的: e --> extend 展开 ; num --> number 数字 --> 展开很多数字就是枚举

PS.仅限理解！千万别被带偏了，枚举的英文单词为 enumerate ；

(一)、枚举类型的定义

还是以星期为例子，想要枚举出星期的枚举类型该如何写呢？

结果如下：

是不是感觉看着跟结构体类型的声明很像，我们来将二者对比一下；

详见上图可知，枚举类型的声明与结构体类型的声明相似，只不过枚举常量之间用 , 分隔开，并且最后一个枚举常量并不需要 , ，而结构体成员之间是用 ; 分隔开来；

枚举常量不需要类型，它们仅仅只是一个字符，写好了之后（枚举类型创建好了之后）便不可以被修改；而结构体成员是具有类型的变量；

question1:枚举类型是否和结构体类型一样，倘若仅仅只是声明类型就不会占用内存空间？

枚举类型在声明的时候不会占用内存空间，只有在利用该枚举类型创建枚举变量的时候才会向内存申请空间来存放数据；

枚举常量作为字符都是有值的，默认从0开始，一次递增1；当然在定义的时候可以为其赋上初始值；

从上图可得知，枚举常量是有值的，并且默认第一个枚举常量得值为0，并且随着枚举常量数量得增多，其值依次在上一个枚举常量值的基础上增加1；

当我们为枚举常量赋值时：

我们再给一个枚举变量赋值：

可见，依次在上一个枚举常量值的基础上增加1的属性仍然存在；

注：此处仅仅是为枚举常量赋值，并不是在修改枚举常量；而之所以这些常量不占内存空间，可能是由于编译器将这些常量以符号的形式存在的；但是枚举类型倘若作为代码存在确实是需要空间来存放的，但这个空间并不是在内存中开辟的（况且内存并不是为每一个常量、符号而开辟空间），故而枚举类型的声明并不会占用内存空间；

question 2:是否可以像使用结构体类型那样使用枚举类型？

可以；使用如下图：

利用枚举类型 enum Day 创建了变量date, 枚举变量date 的取值只能是枚举类型中列举出来的值，不能用其他值给类型为 enum Day 的变量赋值！

(二)、枚举的优点

看了上文，你可能会感觉到枚举常量和#define 定义的标识符常量有点相似，只不过枚举可以一次解决多个；

既然相似为什么还存在枚举呢？或者说枚举的优点有哪些？

枚举的有优点：

1、增加代码的可读性和可维护性

2、与#define 定义的标识符常量比起来，枚举具有类型检查，更加严谨

3、防止命名污染（封装）

4、便于调试

5、便于使用，一次可以定义多个常量；

光看上面枚举的优点，可能有点干巴巴的，下文便结合一些例子来理解；

增加代码的可读性与可维护性

在写通讯录的时候，菜单中对应的功能在switch 语句中是用数字来对应的，这是因为case 后面只能接整型常量表达式；而数字对应相应的功能，需要配合菜单一起看才好理解，但是如果使用枚举常量便可以增加代码的可读性，况且在维护上也更利于维护；

而如若采用了枚举：

与#define 定义的标识符常量比起来，枚举具有类型检查，更加严谨

#define 定义的标识符常量是不具有类型的；而枚举常量是带有类型的；

防止命名污染（封装）
便于调试

#define 定义的标识符常量工作的实质是替换，在调试的过程中就不利于观察细节；

#define 定义的标识符常量在什么时候完成替换的呢？

当你写了一个 .c 文件的时候，此文件是要经过编译、链接，最后生成了 .exe 文件；而在编译的过程中会有一个小过程，叫做预处理；正是在预处理阶段，标识符常量便会完成替换；

调式是在那个过程呢？

我们调试代码调试的是此代码经过预处理、编译、链接产生的 .exe 文件；

但是对于枚举常量来说并不是以替换来实现的，倘若你在代码中使用了枚举常量，在调试的时候仍然可以观察到这些枚举常量的值；故而枚举更便于调试；

使用方便，一次可以定义多个常量；

(三)、枚举的使用

只能拿枚举常量给枚举变量赋值，不然会出现类型的差异；

二、联合

(一)、联合类型的定义

联合体也是一种特殊的结构体类型；

但是此种特殊的结构体类型变量也就是联合变量，包括了一系列的成员，特征是这些成员共用同一块空间。

故而联合也称为共用体；

联合的关键字为 union;

联合类型的声明如下：

这么看，联合体类型的声明除了关键字与结构体类型的声明不太一样，表面上都是一样的；那么联合体成员使用内存空间的情况与结构体变量一样吗？

我们可以测试一下：

我们发现，联合体变量其成员使用内存空间的情况与结构体变量成员使用规则有所不同；下图便是对比：

从上图我们可以得知，联合变量的成员会共用内存（但是联合体变量整体占用的内存需要对齐到最大对齐数的整数倍），而结构体成员在使用内存时存在对齐规则；

利用代码验证一下来联合成员是否真的会共用同一块内存空间？

综上，联合变量相较于结构体变量存在两点不同（只谈使用不谈作用），

在声明上仅仅只是其关键字不同；
以及二者成员使用内存空间的规则不同，联合体变量的成员会共用空间，而结构体变量的成员遵循对齐规则；

看到这你可能就会有疑问了，联合体变量的成员共用内存空间，其数据不能单独存放，那么联合体变量的使用场景是什么呢？

联合体巧妙的运用场景：（例子如上图）有时候会使用到a 所占用的这块空间，而有时候会使用到 b所占用的空间，即联合体变量的成员不会同时使用；于是乎就在一定程度上较少了对空间的使用节省了空间；

当你想在联合体变量 u中成员 a 中存放数据的时候，那便将成员a 所占用的1 byte 的空间给覆盖掉；而当你想在联合体变量 u 中成员 b 中存放数据的时候，那便将成员 b 所占用的 4 byte 的空间给覆盖掉；

(二)、联合的特点

联合体成员是共用一块内存空间的，这样一个联合变量的大小，至少得是最大成员的大小，因为联合体至少得有能力让占用内存空间最大的那个成员能够存放其数据；

调试如下：

从调试的图中，我们可以感知到，联合体成员共用空间的特征；

(三)、联合大小的计算

联合体的大小至少得是其最大成员的大小（请注意“至少”）
当最大成员的大小不是最大对齐数的整数倍的时候，要对齐到最大对齐数的整数倍；

图解分析如下：

成员数组 ch 的对齐是按照其中的元素进行对齐的，而VS编译器默认的对齐数为 8 --> 取其较小值，故而成员 ch 的对齐数为 1；而成员 i 的对齐数为 4 ；--> 此联合体变量 u 的最大对齐数为 4,则其大小必须是 4 的整数倍；

注：vs 编译器中默认对齐数为8；

在vs 编译器上对于一个变量对齐数的计算，在此变量自身大小与默认对齐数之间取得较小值，就为此变量的对齐数；

倘若在一个编译器上没有默认对齐数的概念，那么该变量自身的大小便为其对齐数的大小；

question 1:你可能会对上面数组 ch 计算所得的对齐数为1 有所疑惑；

你可能会这样想，数组ch 的类型为 char [6] , 所占空间的大小为 6byte ,vs 编译器默认的对齐数为 8 --> 取其较小值，则会认为成员 ch 的对齐数为6；

实际上不是这样想的，首先数组是一类元素的集合，元素与元素就是单独的个体，只不过放在一个数组之中，而此处讨论的是数组 ch 在对齐时的对齐数为多少，故而应该看的是数组中元素的大小；

ch 数组元素的大小为 1，vs 编译器默认的对齐数为8 --> 取其较小值：1；故而成员 ch 的对齐数为1 ；

注：不要天真地以为联合体的大小为其最大成员的大小；

再举一个例子，加深对联合大小的计算；