inflight 守恒算法的实现和仿真

news2024/11/17 6:51:55

前面介绍过，只要某条流的 inflt 在 bdp 之外再增加一个相等的余量 I，即 inflt = bdp + I，比如 I = 2，I = 3，…，就一定会收敛到公平，且不会占据过多 buffer，因此 rtt 不会膨胀，I 的大小影响收敛速度，I 越大，收敛越快，但 buffer 占据也更多，I 越小，收敛越慢，但 buffer 占据更少，所以效率和公平的 tradeoff 在此体现。

记住这个简洁的结论，然后将 I 调整为动态的负反馈，就是一个新算法，该算法占据 “一定量” 的 buffer 而不是像 aimd 那样抖动，占据 buffer 的大小由 I 的均值决定。平稳压倒一切，抖动是低效的根源，始终占据一定量的 buffer 是可以接受的，通过调参可以将这个 “一定量” 压到尽可能小。

简单用 c 实现了一版 inflight 守恒算法，非常简洁：

#include <stdio.h>
#include <stdlib.h>

#define BW_FILTER_LEN 10

double RTPROP = 1;
double C = 100.0; // bottleneck_link_bw
double I = 0.0;

struct es {
  double E;
  double bw;
};

struct ebest_flow {
  int index;               /* flow identifier */
  int status;
  double I;
  double inflt;
  double min_rtt;
  double srtt;
  double sending_bw;       /* current receive bw */
  double receive_bw;       /* current receive bw */
  struct es max_e;           /* current estimated bw */
  struct es e_samples[BW_FILTER_LEN];
  int phase_offset;
};

struct ebest_flow f1;
struct ebest_flow f2;
struct ebest_flow f3;
struct ebest_flow f4;

int t = 0;
int bw_filter_index = 0;

#define max(a, b) (a > b) ? (a) : (b)
#define min(a, b) (a < b) ? (a) : (b)

void ebest_set_max_e(struct ebest_flow *f)
{
  int i = 0;

  f->max_e.bw = 0;
  for (i = 0; i < BW_FILTER_LEN; i++) {
    f->max_e.E = max(f->max_e.E, f->e_samples[i].E);
    f->max_e.bw = f->e_samples[i].bw;
  }
  f->I = 0.7 * f->I + 0.3 * 40 * f->min_rtt * f->max_e.bw/(20 * f->min_rtt + f->max_e.bw * f->srtt) * (f->min_rtt / f->srtt);
}

void ebest_update_maxbw_minrtt(struct ebest_flow *f, double rtt)
{
  rtt = (rtt > RTPROP)?:RTPROP;
  f->e_samples[bw_filter_index].E = f->receive_bw / rtt;
  f->e_samples[bw_filter_index].bw = f->receive_bw;
  ebest_set_max_e(f);
  if (rtt <= f->min_rtt) {
    f->srtt = f->min_rtt = rtt;
  } else {
    f->srtt = rtt;
  }
}

void ebest_update_sending_bw(struct ebest_flow *f)
{

  f->inflt = f->max_e.bw * f->min_rtt + f->I;
  printf("#### f: %d  %.3f\n", f->index, f->I);
  f->sending_bw = f->max_e.bw;
  printf("flow %d phase: %d max_bw: %.3f sending_bw: %.3f\n",
         f->index, 0, f->max_e.bw, f->sending_bw);
}

void simulate_one_phase(int i)
{
  double rtt;
  //if (i == 1500)
  //  C = 160;
  //if (i == 2500)
  //  C = 40;

  ebest_update_sending_bw(&f1);
  ebest_update_sending_bw(&f2);
  ebest_update_sending_bw(&f3);
  ebest_update_sending_bw(&f4);

  printf("t= %04d sending: f1: %.3f f2: %.3f f3: %.3f f4: %.3f\n",
         t, f1.sending_bw, f2.sending_bw, f3.sending_bw, f4.sending_bw);

  double total_I = 0;
  if (i < 1000) {
    rtt = (f1.inflt + f2.inflt + f3.inflt) / C;
    f1.receive_bw = C * f1.inflt / (f1.inflt + f2.inflt + f3.inflt);
    f2.receive_bw = C * f2.inflt / (f1.inflt + f2.inflt + f3.inflt);
    f3.receive_bw = C * f3.inflt / (f1.inflt + f2.inflt + f3.inflt);
    f4.receive_bw = 0;
    f4.max_e.bw = 0;
    f4.inflt = 0;
    if (i == 999) {
      f4.max_e.bw = 0.1 * C;
      f4.inflt = 0.1 * C * RTPROP + I;
      f4.I = I;
      f4.receive_bw = 0.1 * C;

      printf("@@@@### time: %d  f1: %.3f  f2: %.3f  f3: %.3f  f4: %.3f \n", t, f1.inflt, f2.inflt, f3.inflt, f4.inflt);
    }
    total_I = f1.I + f2.I + f3.I;
    printf("t= %04d  remain: f1: %.3f f2: %.3f f3: %.3f f4: %.3f\n",
           t, f1.I, f2.I, f3.I, total_I);
  } else if (i >= 1000 && i < 2000) {
    rtt = (f1.inflt + f2.inflt + f3.inflt + f4.inflt) / C;
    f1.receive_bw = C * f1.inflt / (f1.inflt + f2.inflt + f3.inflt + f4.inflt);
    f2.receive_bw = C * f2.inflt / (f1.inflt + f2.inflt + f3.inflt + f4.inflt);
    f3.receive_bw = C * f3.inflt / (f1.inflt + f2.inflt + f3.inflt + f4.inflt);
    f4.receive_bw = C * f4.inflt / (f1.inflt + f2.inflt + f3.inflt + f4.inflt);
    if (i < 1100) {
      printf("@@@@### time: %d  f1: %.3f  f2: %.3f  f3: %.3f  f4: %.3f \n", t, f1.inflt, f2.inflt, f3.inflt, f4.inflt);
    }
    total_I = f1.I + f2.I + f3.I + f4.I;
    printf("t= %04d  remain: f1: %.3f f2: %.3f f3: %.3f f4: %.3f\n",
           t, f1.I, f2.I, f3.I, total_I);
  } else {
    rtt = (f1.inflt + f2.inflt) / C;
    f1.receive_bw = C * f1.inflt / (f1.inflt + f2.inflt);
    f2.receive_bw = C * f2.inflt / (f1.inflt + f2.inflt);
    f3.receive_bw = 0;
    f4.receive_bw = 0;
    f3.max_e.bw = 0;
    f4.max_e.bw = 0;
    f3.inflt = 0;
    f4.inflt = 0;
    total_I = f1.I + f2.I;
    printf("t= %04d  remain: f1: %.3f f2: %.3f f3: %.3f f4: %.3f\n",
           t, f1.I, f2.I, f3.I, total_I);
  }
  if (rtt < RTPROP)
    rtt = RTPROP;

  printf("t= %04d receive: f1: %.3f f2: %.3f f3: %.3f f4: %.3f\n",
         t, f1.receive_bw, f2.receive_bw, f3.receive_bw, f4.receive_bw);

  ebest_update_maxbw_minrtt(&f1, rtt);
  ebest_update_maxbw_minrtt(&f2, rtt);
  ebest_update_maxbw_minrtt(&f3, rtt);
  ebest_update_maxbw_minrtt(&f4, rtt);

  printf("t= %04d  max_bw: f1: %.3f f2: %.3f f3: %.3f f4: %.3f\n",
         t, f1.max_e.bw, f2.max_e.bw, f3.max_e.bw, f4.max_e.bw);
  printf("t= %04d  inflt: f1: %.3f f2: %.3f f3: %.3f f4: %.3f\n",
         t, f1.inflt, f2.inflt, f3.inflt, f4.inflt);
  printf("t= %04d  min_rtt: f1: %.3f f2: %.3f f3: %.3f f4: %.3f\n",
         t, rtt, f2.min_rtt, f3.min_rtt, f4.min_rtt);

  t++;
  bw_filter_index = (bw_filter_index + 1) % BW_FILTER_LEN;
}

int main(int argc, char *argv[])
{
  int i = 0;

  if (argc > 1) I = atof(argv[1]);

  f1.index = 1;
  f2.index = 2;
  f3.index = 3;
  f4.index = 4;

  f1.max_e.bw = 0.9 * C;
  f2.max_e.bw = 0.3 * C;
  f3.max_e.bw = 0.6 * C;

  f1.max_e.E = f1.max_e.bw / RTPROP;
  f2.max_e.E = f2.max_e.bw / RTPROP;
  f3.max_e.E = f3.max_e.bw / RTPROP;

  f1.I = I;
  f2.I = I;
  f3.I = I;
  f4.I = 0;

  f1.srtt = f1.min_rtt = RTPROP;
  f2.srtt = f2.min_rtt = RTPROP;
  f3.srtt = f3.min_rtt = RTPROP;
  f4.srtt = f4.min_rtt = RTPROP;

  f1.inflt = 0.1 * C * RTPROP;
  f2.inflt = 0.3 * C * RTPROP;
  f3.inflt = 0.6 * C * RTPROP;

  f1.e_samples[BW_FILTER_LEN - 1] = f1.max_e;
  f2.e_samples[BW_FILTER_LEN - 1] = f2.max_e;
  f3.e_samples[BW_FILTER_LEN - 1] = f3.max_e;

  for (i = 0; i < 3000; i++) {
    simulate_one_phase(i);
  }

  return 0;
}

算法和建模分别参见 inflight 守恒背后的哲学 与 inflight 守恒数学建模.

这个算法的核心只需要设置 remain 余量，剩下的跟踪 E_best = max(bw / delay) 即可，因此 remain 一定是个负反馈方程：

R e m a i n = α ⋅ R T T m i n ⋅ B W w h e n _ E _ b e s t β ⋅ R T T m i n + B W w h e n _ E _ b e s t ⋅ R T T s m o o t h ⋅ R T T m i n R T T s m o o t h Remain=\dfrac{\alpha\cdot RTT_{min}\cdot BW_{when\_E\_best}}{\beta \cdot RTT_{min}+BW_{when\_E\_best}\cdot RTT_{smooth}}\cdot \dfrac{RTT_{min}}{RTT_{smooth}} Remain=β⋅RTTmin​+BWwhen_E_best​⋅RTTsmooth​α⋅RTTmin​⋅BWwhen_E_best​​⋅RTTsmooth​RTTmin​​

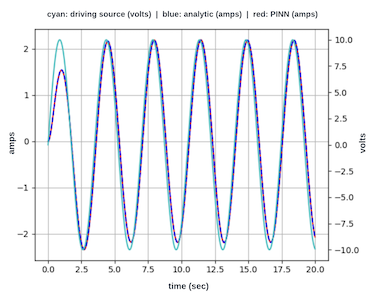
效果如下：
在这里插入图片描述

明显有负反馈效果，但还是需要增加自由度，继续调参，我需要的效果是无论多少条流，所有流的 Remain 之和在一个有限范围内。

而 inflt 收敛效果如下：
在这里插入图片描述

rtt 平稳且并未膨胀：
在这里插入图片描述

浙江温州皮鞋湿，下雨进水不会胖。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/2076106.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

html+css网页设计 动漫 海贼王14个页面

html+css网页设计 动漫 海贼王14个页面

htmlcss网页设计 动漫 海贼王14个页面 网页作品代码简单&#xff0c;可使用任意HTML编辑软件&#xff08;如&#xff1a;Dreamweaver、HBuilder、Vscode 、Sublime 、Webstorm、Text 、Notepad 等任意html编辑软件进行运行及修改编辑等操作&#xff09;。 获取源码 1&#x…
阅读更多...
开放式耳机对耳朵好吗？开放式耳机哪个品牌好？

开放式耳机对耳朵好吗？开放式耳机哪个品牌好？

许多人在选择开放式耳机时并不了解如何选购。对开放式耳机也不是很了解&#xff0c;所以我在这里做个简单的科普和分享。今天跟大家聊聊开放式耳机会伤害耳朵吗&#xff1f;开放式耳机有什么好处&#xff1f;等等&#xff0c;下面一起来看看吧~ 开放式耳机是什么意思&#xff1…
阅读更多...
如何有效激活微信陌生客户：加好友后的沟通策略!

如何有效激活微信陌生客户：加好友后的沟通策略!

在当今这个数字化时代&#xff0c;微信已成为我们与客户建立联系的重要桥梁。对于许多企业和个人而言&#xff0c;成功添加陌生客户到微信列表只是第一步&#xff0c;真正的挑战在于如何有效激活这些潜在客户&#xff0c;转化为实际交易或长期关系。 下面分享一些沟通策略&…
阅读更多...
oracle ONS configuration failed NoserversAvailable:Subscription time out导致应用起不来

oracle ONS configuration failed NoserversAvailable:Subscription time out导致应用起不来

java.lang.IllegalArgumentException:ONS configuration failed Caused by: oracle.ons.NoserversAvailable:Subscription time out ##已部署到服务器解决方案&#xff1a; 修改这个2个jar包后缀 ##在项目工程里面&#xff0c;<artifactId>ojdbc8</artifactId> m…
阅读更多...
具有强制函数的物理信息神经网络

具有强制函数的物理信息神经网络

图片由 agsandrew 在 iStock 上发布 一、说明 在物理学、数学、经济学、工程学和许多其他领域&#xff0c;微分方程根据变量的导数来描述函数。简而言之&#xff0c;当涉及一个变量相对于其他变量的变化率时&#xff0c;你可能会找到一个微分方程。许多示例描述了这些关系。微分…
阅读更多...
debian12 - install and config telnet

debian12 - install and config telnet

文章目录 debian12 - install and config telnet概述笔记配置文件END debian12 - install and config telnet 概述 前面实验&#xff0c;在xinetd中指定telnet服务&#xff0c;查看状态时&#xff0c;看到telnet服务bind失败。 直接从其他计算机来连telnet又是正常的&#xf…
阅读更多...
随记-部署flink-1.16.3、jdk-11.0.19、zookeeper-3.4.13、kafka_2.12-2.2.2

随记-部署flink-1.16.3、jdk-11.0.19、zookeeper-3.4.13、kafka_2.12-2.2.2

一、部署flink-1.16.3、jdk-11.0.19、zookeeper-3.4.13、kafka_2.12-2.2.2 #软件下载 https://archive.apache.org/dist/kafka/2.2.2/kafka_2.12-2.2.2.tgz https://archive.apache.org/dist/zookeeper/zookeeper-3.4.13/zookeeper-3.4.13.tar.gz https://archive.apache.org/…
阅读更多...
Clustering-Guided Class Activation for WeaklySupervised Semantic Segmentation

Clustering-Guided Class Activation for WeaklySupervised Semantic Segmentation

pdf&#xff1a;https://ieeexplore.ieee.org/stamp/stamp.jsp?tp&arnumber10381698 code&#xff1a;https://github.com/DCVL-WSSS/ClusterCAM 摘要&#xff1a; 基于transformer的弱监督语义分割(WSSS)方法利用其捕获全局上下文的强大能力得到了积极的研究。然而&am…
阅读更多...
day8JS-作用域

day8JS-作用域

1. 变量的作用域(变量函数) 作用域是变量的可作用范围&#xff0c;变量只有在自己的作用域下才会生效。 函数会产生作用域&#xff0c;在函数内定义的变量只能在函数内使用。 2. 作用域分类 局部作用域&#xff1a; 函数内定义的变量和形参的作用域就是局部作用域&#xff1b;这…
阅读更多...
【Hot100】LeetCode—207. 课程表

【Hot100】LeetCode—207. 课程表

目录 1- 思路有向图记录入度数组出度列表 2- 实现⭐207. 课程表——题解思路 3- ACM 实现 题目连接&#xff1a;207. 课程表 1- 思路 有向图记录入度数组出度列表 根据输入① 构造遍历构造入度数组② 构造出度列表根据入度数组为 0 的数 加入到 队列中&#xff0c;进行处理 2…
阅读更多...
在线拼图用什么软件？5款顶级照片拼接工具

在线拼图用什么软件？5款顶级照片拼接工具

照片拼接在一起用什么软件&#xff1f;当你想全景展现山西应县木塔的震撼之美时&#xff0c;5款精选照片拼接软件能帮你解锁全新视角。 这座千年古塔&#xff0c;巍峨耸立&#xff0c;细节之处尽显匠心独运。而通过拼接技术&#xff0c;每一块木构的精致、每一层塔檐的飞翘都能…
阅读更多...
OpenBayes 教程上新 | 青岛小哥焦恩俊版二郎神来袭，MuseV + MuseTalk 分分钟实现高质量数字人制作！

OpenBayes 教程上新 | 青岛小哥焦恩俊版二郎神来袭，MuseV + MuseTalk 分分钟实现高质量数字人制作！

使用传统的数字人训练方案生成一个高质量的数字人&#xff0c;常常需要大量的时间和算力资源&#xff0c;同时对训练素材的要求也较高&#xff0c;如果想要达到良好的唇形一致效果&#xff0c;通常需要数小时乃至更久。 MuseV 和 MuseTalk 的出现为数字人领域带来了新的突破&a…
阅读更多...
【Canvas与桌面】十字网格黑灰背景(1920x1080)

【Canvas与桌面】十字网格黑灰背景(1920x1080)

【成图】 【代码】 <!DOCTYPE html> <html lang"utf-8"> <meta http-equiv"Content-Type" content"text/html; charsetutf-8"/> <head><title>十字网格黑灰背景(1920x1080)</title><style type"te…
阅读更多...
iphone被锁定怎么解锁？iPhone密码锁解锁办法分享

iphone被锁定怎么解锁？iPhone密码锁解锁办法分享

在忙碌的生活中&#xff0c;有时我们可能会遇到一些“小插曲”&#xff0c;比如苹果手机被锁定&#xff0c;iPhone被锁定是一个常见的问题&#xff0c;可能是由于忘记密码、多次输入错误密码或设备被远程锁定等原因造成的。 本文将介绍解锁被锁定的iPhone的方法以及注意事项&a…
阅读更多...
【网络安全】IDOR之请求包分析

【网络安全】IDOR之请求包分析

未经许可，不得转载。 文章目录 正文正文 某在线游戏平台，在开始测试时，我访问了 /profile 页面（个人资料页面），然后查看 Burp 历史记录，想查看有多少隐藏的请求。 可以看到一个HTTP 的 OPTIONS 方法的请求包： 从图中看到，该请求包含两个参数：player_id_or_name（用…
阅读更多...
OpenHarmony源码解析之电话子系统——通话流程

OpenHarmony源码解析之电话子系统——通话流程

一、简介 OpenAtom OpenHarmony&#xff08;以下简称“OpenHarmony”&#xff09;电话子系统为 OS 提供了基础的无线通信能力。 支持 TD-LTE/FDD-LTE/TD-SCDMA/WCDMA/EVDO/CDMA1X/GSM 等网络制式的通信模块&#xff0c;能够提供高速的无线数据传输、互联网接入等业务&#xf…
阅读更多...
c++栈和队列（stack和queue）

c++栈和队列（stack和queue）

前言 栈和队列是两个极其相似的数据结构&#xff0c;栈具有先进后出的特性&#xff0c;队列具有先进先出的特性。今天我们就来简单的介绍一下栈和队列这两数据结构&#xff0c;其中队列我们介绍普通队列、双端队列&#xff08;了解&#xff09;和优先级队列&#xff08;其实这…
阅读更多...
C++从入门到起飞之——vector模拟实现 全方位剖析！

C++从入门到起飞之——vector模拟实现 全方位剖析！

​ &#x1f308;个人主页&#xff1a;秋风起&#xff0c;再归来~&#x1f525;系列专栏&#xff1a;C从入门到起飞 &#x1f516;克心守己&#xff0c;律己则安 目录 1、vector的成员变量 2、迭代器 3、size与capacity 4、[]运算符重载 5、reserve 6、push_bac…
阅读更多...
LSTM结合时序异常检测直接写！小论文闭着眼睛发！

LSTM结合时序异常检测直接写！小论文闭着眼睛发！

还在愁小论文&#xff1f;不如考虑考虑这个方向&#xff1a;LSTM时间序列异常检测。 这是个比较活跃且热门的研究方向&#xff0c;因为LSTM具有非常优秀的时序数据深度处理能力&#xff0c;能够灵活适应不同复杂度的数据&#xff0c;给我们提供高精度的预测结果&#xff0c;在…
阅读更多...
时间继电器和定时器

时间继电器和定时器

一、概述 1.时间继电器是可以在设定的定时周期内或周期后闭合或断开触点的元器件。 2.时间继电器上可设定的定时周期数量有限&#xff0c;多为一个或两个。定时时长从0.02s至300h(根据产品型号范围不同)。 3.定时器可以理解为一台钟表&#xff0c;它在某个时间点上闭合(断开…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023