图片由 agsandrew 在 iStock 上发布

一、说明

        在物理学、数学、经济学、工程学和许多其他领域，微分方程根据变量的导数来描述函数。简而言之，当涉及一个变量相对于其他变量的变化率时，你可能会找到一个微分方程。许多示例描述了这些关系。微分方程的解通常是通过解析或数值方法得出的。

        虽然推导出解析解可能是一项乏味的任务，或者在某些情况下是一项不可能完成的任务，但物理信息神经网络 （PINN） 绕过解析过程，直接从微分方程生成解。这种求解微分方程的创新方法是该领域的重要发展。

二、关于电路微分方程

作者之前的一篇文章使用 PINN 来查找描述简单电子电路的微分方程的解。本文探讨了在用 force 函数驱动电路时寻找解决方案的更具挑战性的任务。考虑以下串联的电子电路，它由电阻 R、电容 C、电感 L 和正弦电压源 V sin（ωt） 组成。该电路中电流 i（t） 的行为由公式 1 描述，公式 1 是一个具有强迫函数 Vω/L cos（ωt） 的二阶非齐次微分方程。

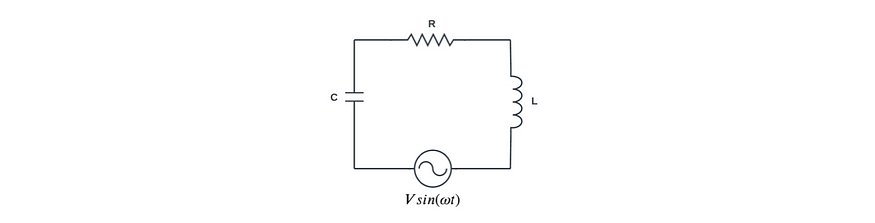
图 1：带正弦电压源的 RLC 电路

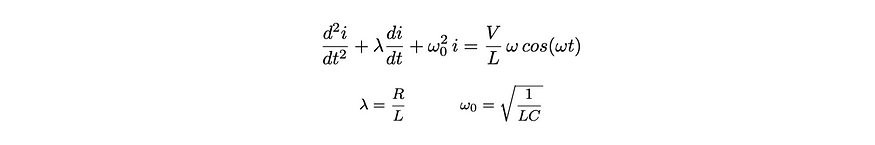
方程 1 

三、分析解决方案

        方程 1 的解析解需要根据 λ 和 ω₀ 之间的关系求解三种情况的方程。如下所示，每个公式都会产生一个复杂而独特的 i（t） 公式。在稍后的结果中介绍的测试中，这些解决方案将与 PINN 生成的结果进行比较。PINN 将直接从微分方程生成解，而不考虑这些情况。

（作者使用拉普拉斯变换技术的详细分析解决方案可在此处获得。

        情况 1：欠阻尼 （λ/2 < ω₀)

阻尼是指电路从其起始传输过渡到平衡的速度。欠阻尼响应会尝试快速过渡，但通常会在达到平衡之前在过冲和下冲之间循环。

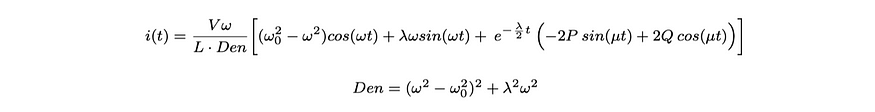
方程 2

情况 2：过阻尼 （λ/2 >ω₀)

过阻尼响应从开始传输缓慢过渡到平衡，而不会经历过冲和下冲的循环。

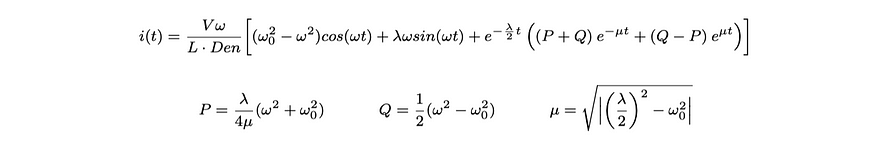
方程 3

情况 3：临界阻尼 （λ/2 = ω₀)

临界阻尼响应介于欠阻尼和过阻尼之间，提供从开始传输到平衡的最快响应。

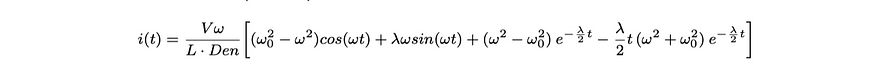
方程 4

四、PINN 解决方案

        PyTorch 代码可在此处获取。

        神经网络通常使用成对的输入和所需的输出进行训练。输入应用于神经网络，反向传播调整网络的权重和偏差以最小化目标函数。目标函数表示神经网络输出与所需输出相比的误差。

        相比之下，PINN 的目标函数需要三个分量：一个残差分量 （obj rₑs） 和两个初始条件分量（obj init₁ 和 obj init₂）。这些组合起来生成目标函数：

方程 5

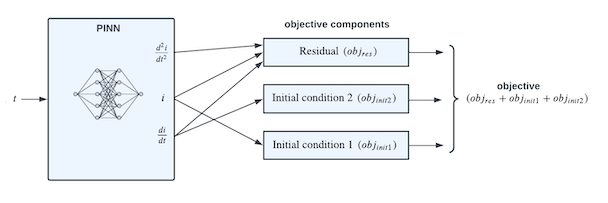
PINN 目标函数

残余

残差分量是物理信息发挥作用的地方。此组件包含输出的导数，约束网络以符合定义的微分方程。残差（公式 6）是通过重新排列公式 1 形成的。

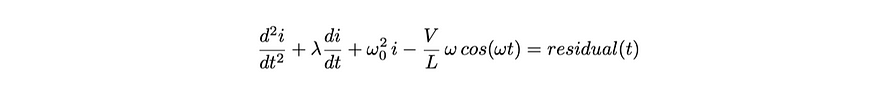
方程 6

在训练期间，t 的值会呈现给神经网络的输入，从而产生残差。然后，反向传播会将所有训练点上目标的残差分量减少到接近 0 的最小值。残差分量由下式给出：

方程 7

公式 6 所需的一阶和二阶导数 di/dt 和 d²i/dt² 由 PyTorch 和 TensorFlow 神经网络平台中的自动微分函数提供。

初始条件 1

在这个电路示例中，第一个初始条件要求 PINN 的输出 i（t） = 0，当输入 t = 0 时。这是由于正弦源 V sin（t） = 0 在 t = 0 时，导致电路中没有电流流动。初始条件 1 的目标分量由公式 8 给出。在训练期间，反向传播会将此分量减少到接近 0 的值。

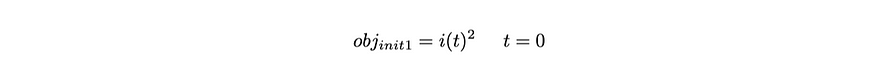
方程 8

初始条件 2

第二个初始条件要求当输入 t = 0 时，L di/dt = 0。它源自基尔霍夫电压定律（即闭环周围的电压降之和为零）。具体来说，当 t = 0 时，电路中存在以下条件：

• 电压源 V sin（ωt） = 0
• 电容器 C 的初始电荷为 Q = 0 ，产生电容器电压为 V_cap = Q/C = 0
• 电阻 R 两端的电压为 V_res = iR = 0，因为 i（t） = 0（初始条件 1）
• 电感 L 两端的电压为 V_ind = L di/dt
• 在上述条件下，电路周围的电压降之和减小到 L di/dt = 0

初始条件 2 的目标分量由公式 9 给出。反向传播会将此组件减少到接近 0 的值。

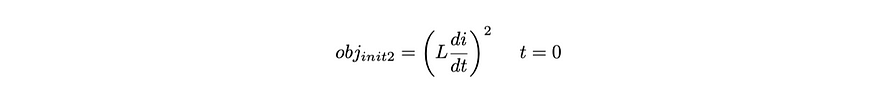
方程 9

目标图

下图显示了训练期间 goal 值的减少情况：

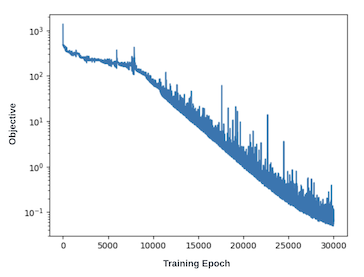
目标图

五、结果

        以下测试用例将经过训练的 PINN 的响应与每个案例的相应分析解进行比较。如上所述，选择 circuit component 值来产生欠阻尼、过阻尼和临界阻尼响应的条件。所有三种情况均由 V = 10 伏和 ω = 1.8 弧度/秒的正弦电压源驱动。对于每种情况，电容器和电感值分别为 C = 0.3 法拉和 L = 1.51 亨利。下面针对每种情况记录了电阻器 R 的值。

欠阻尼
（R = 1.2 欧姆)

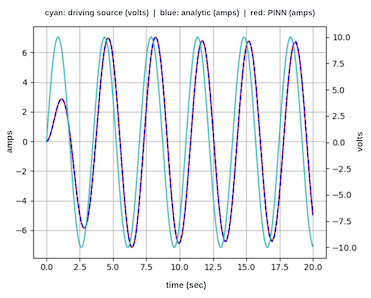
欠阻尼测试用例

过阻尼
（R = 6.0 欧姆)

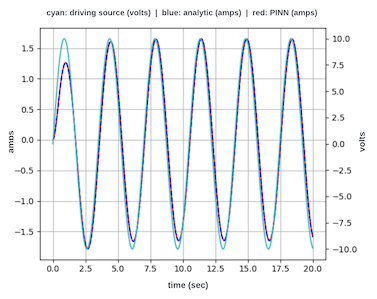
过阻尼测试用例

临界阻尼
（R = 4.487 欧姆)

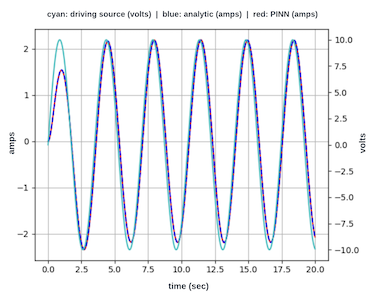
临界阻尼测试用例

六、结论

        在本文中，使用具有自定义目标函数的神经网络成功求解了描述由正弦源驱动的电子电路的微分方程。通常，微分方程的解是通过繁琐的分析过程或数值得出的。这里提供的示例表明，神经网络可以以简单有效的方式准确地求解这些方程。如三个测试用例所示，神经网络响应与解析解相同。

七、附录：PINN 培训说明

• PINN 结构：
  - 输入层，1 个输入
  - 隐藏层，128 个神经元具有 GELU 激活
  - 隐藏层，128 个神经元具有 GELU 激活
  - 输出层，1 个神经元具有线性激活
• PINN 在 0 到 20 秒的时域中使用 220 个点进行训练。点数由域的持续时间和每秒点数的超参数控制，对于测试用例，该超参数设置为 11 点/秒。该值为 ω = 1.8 的正弦驱动源的每个周期提供了足够数量的训练点。对于更高的 ω 值，每秒需要更多的点，例如，ω = 4.0 需要 25 点/秒。
• PINN 分批训练，每批 32 个点，这些点从所有训练点的集合中采样。训练点在每个 epoch 随机洗牌。
• 学习率在训练开始时从 0.01 开始，每 2000 个 epoch 降低 0.75 倍。
• 目标图是训练成功的重要指标。随着训练的进行，目标应减少几个数量级，并在接近 0 的小值处触底。如果训练无法产生此结果，则需要调整超参数。建议先尝试增加 epoch 的数量，然后增加每秒的训练点数。