哈夫曼编码原理
哈夫曼编码属于一种基于字符出现频率的贪心算法,其通过构建哈夫曼树,为文本中的每一个字符赋予独一无二的二进制编码。频率较高的字符会被分配较短的编码,而频率较低的字符则会被分配较长的编码,以此达成压缩数据的目标。
构建哈夫曼树的步骤
- 统计频率:统计文本中各个字符的出现次数。
- 选择频率最低的节点:从统计结果中选择频率最低的两个节点,并将其作为新节点的左右子节点,并将构成的新节点放回。
- 构建哈夫曼树:重复步骤2,直到所有节点都被合并为一棵树。
编码与解码过程
- 编码:利用哈夫曼树为每个字符生成编码。从根节点起始,向左行进表示“0”,向右行进表示“1”,一直抵达叶子节点,叶子节点所对应的字符编码便是该字符的哈夫曼编码。
- 解码:依据编码逆向遍历哈夫曼树,从根节点出发,读取一位编码,向左走代表“0”,向右走代表“1”,直至抵达叶子节点,输出该节点的字符,而后回退至根节点继续解码。
示例
首先我们给定一个示例文本,并统计各字符的频率

然后选择频率最低的两个节点进行合并
这里因为有多个频率为1的节点,我直接全部连上了(连的方式不唯一,只要连接时选择频率最小的即可)

刚才剩下来的’!'也是频率为1的,随便找个最小的连上就行
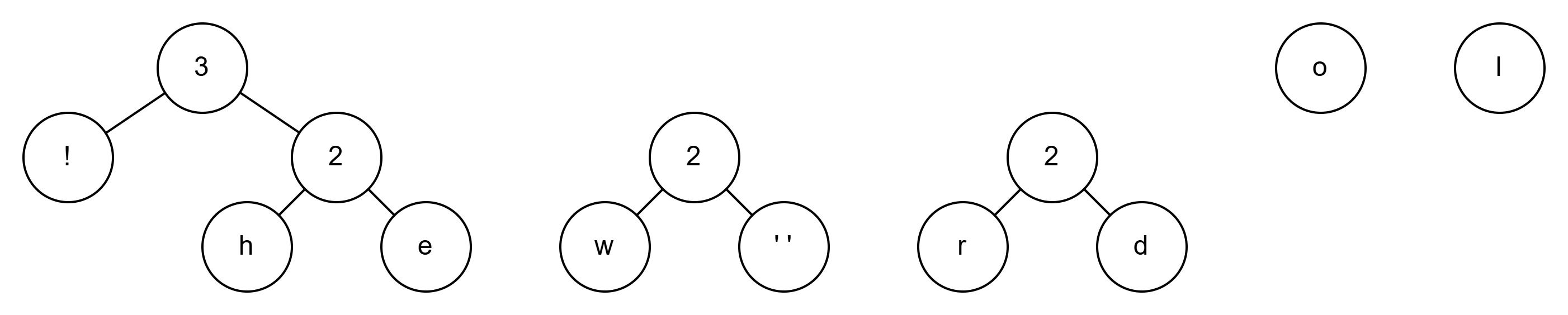
现在2是最小的了,就把2连起来变成4
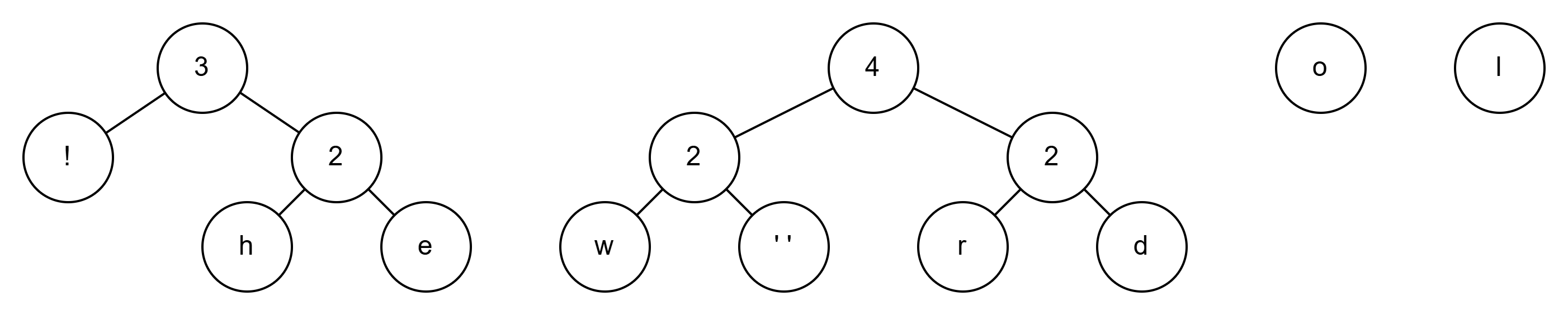
现在剩下的节点权重为2,3,3,4
所以继续2+3=5
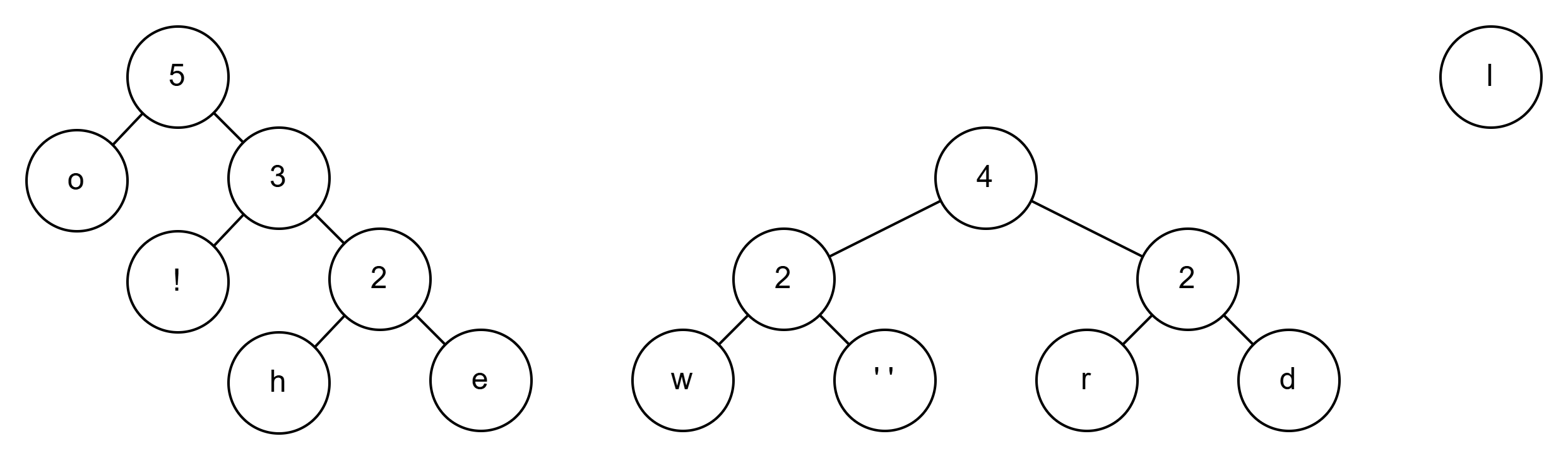
3+4=7
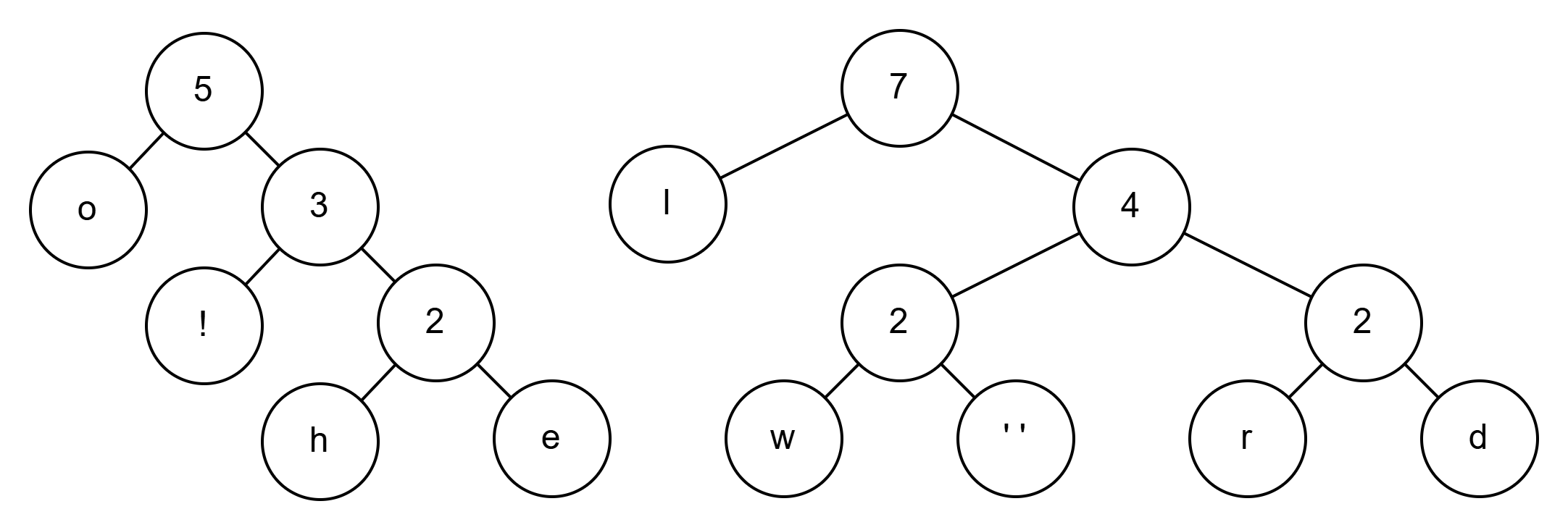
5+7=12
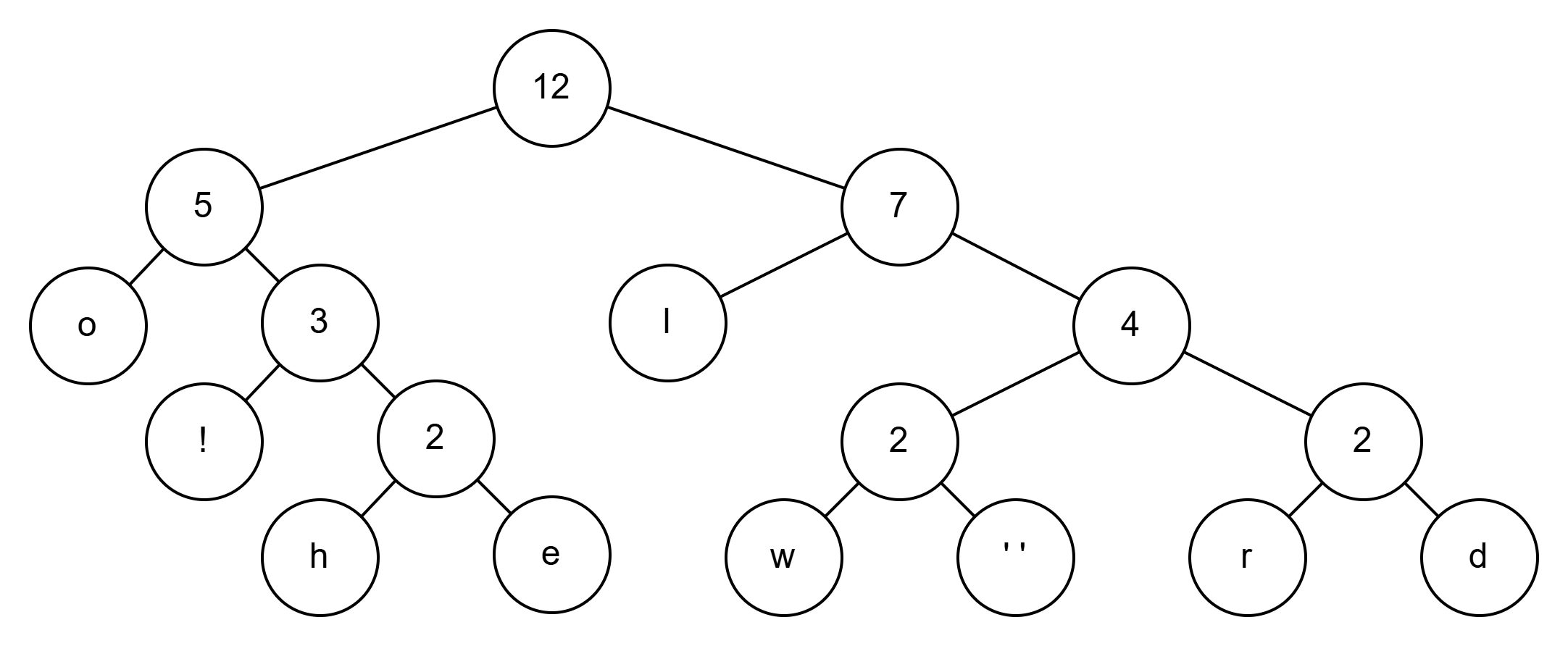
这样就构建完成了,我们可以根据这棵树得到编码
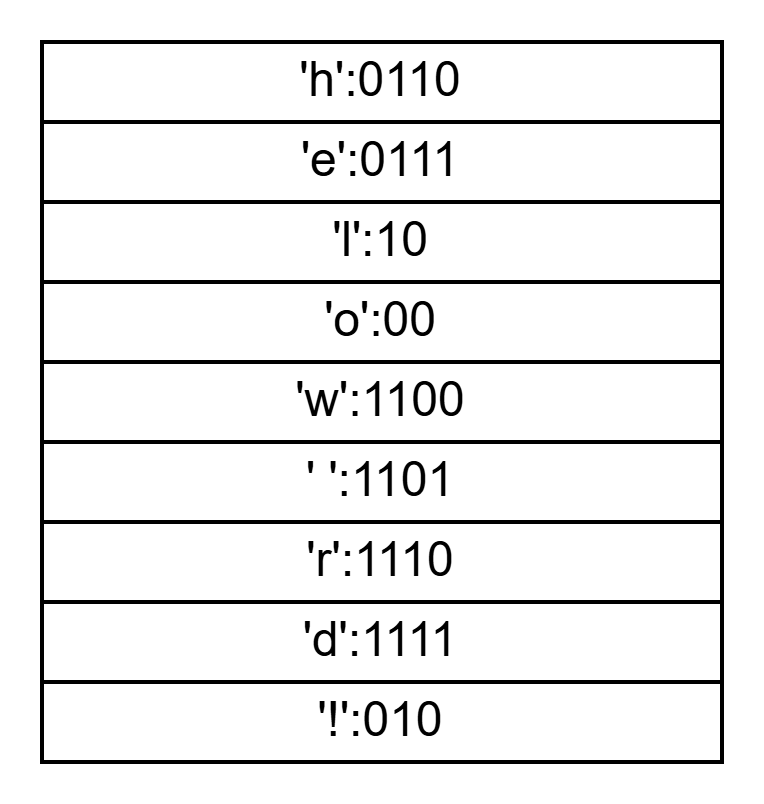
结果不唯一,与迭代过程中的选择顺序有关
问题
可能有人会想,我原本1个字符编码后长度不为1了,那不是没有起到压缩的效果吗?
但是我们可以用位来存储,根据不同的字符集,原本一个字符需要7位,8位,16,位甚至32位,现在可以降低出现频率更高的字符的编码长度,那么反映在需要压缩的文本中,压缩比就很可观了。虽然可能会导致低频字符的编码长度变长,但是其频率低,对压缩结果影响不大。所以最终能起到压缩的效果
Python 实现哈夫曼编码
以下是我用Python实现的一个示例
其中在序列化和反序列化的时候因为我们只关心树的结构,所以没有对weight进行处理
# -*- coding: utf-8 -*-
"""
Huffman编码
"""
import os
from collections import Counter
from heapq import *
from typing import Union
from bitarray import bitarray
class HuffmanNode:
"""
Huffman节点基类
"""
def __init__(self, weight, ):
"""
初始化节点权重
:param weight: 节点权重
"""
self.weight = weight
def __lt__(self, other):
"""
小于运算符重载,用于比较节点权重
:param other: 另一个节点
:return: 如果当前节点权重小于另一个节点的权重,则返回True
"""
return self.weight < other.weight
def __eq__(self, other):
"""
等于运算符重载,用于比较节点权重
:param other: 另一个节点
:return: 如果当前节点权重等于另一个节点的权重,则返回True
"""
return self.weight == other.weight
def __gt__(self, other):
"""
大于运算符重载,用于比较节点权重
:param other: 另一个节点
:return: 如果当前节点权重大于另一个节点的权重,则返回True
"""
return self.weight > other.weight
class HuffmanTreeNode(HuffmanNode):
"""
Huffman树节点类,继承自HuffmanNode
"""
def __init__(self, left, right, weight=None):
"""
初始化树节点,包含左右子节点和节点权重
:param left: 左子节点
:param right: 右子节点
:param weight: 节点权重,可选
"""
super().__init__(weight)
self.left = left
self.right = right
class HuffmanLeafNode(HuffmanNode):
"""
Huffman叶子节点类,继承自HuffmanNode
"""
def __init__(self, char, weight=None):
"""
初始化叶子节点,包含字符和节点权重
:param char: 字符
:param weight: 节点权重,可选
"""
super().__init__(weight)
self.char = char
class HuffmanTree:
"""
Huffman树类,提供编码和解码功能
"""
@staticmethod
def create_tree(data: dict):
"""
根据给定的数据创建Huffman树
:param data: 包含字符和权重的字典
:return: 返回Huffman树的根节点
"""
node = [
HuffmanLeafNode(key, value) for key, value in data.items()
]
heapify(node)
while len(node) > 1:
left = heappop(node)
right = heappop(node)
heappush(node, HuffmanTreeNode(left, right, left.weight + right.weight))
else:
return heappop(node)
@staticmethod
def save_tree_to_file(fp, tree):
"""
将Huffman树保存到文件中
:param fp: 文件路径
:param tree: Huffman树的根节点
"""
def save_helper(f, tree):
if isinstance(tree, HuffmanLeafNode):
f.write('L')
f.write(f'{tree.char}')
elif isinstance(tree, HuffmanTreeNode):
f.write('N')
save_helper(f, tree.left)
save_helper(f, tree.right)
with open(fp, 'w', encoding='utf-8') as f:
save_helper(f, tree)
@staticmethod
def load_tree_from_file(fp):
"""
从文件中加载Huffman树
:param fp: 文件路径
:return: 返回Huffman树的根节点
"""
def load_helper():
identifier = f.read(1)
if identifier == 'L':
char = f.read(1)
return HuffmanLeafNode(char)
elif identifier == 'N':
left = load_helper()
right = load_helper()
return HuffmanTreeNode(left, right)
with open(fp, 'r', encoding='utf-8') as f:
return load_helper()
@staticmethod
def get_code(root: Union[HuffmanTreeNode, HuffmanLeafNode]):
"""
获取Huffman编码字典
:param root: Huffman树的根节点
:return: 包含字符和对应编码的字典
"""
if isinstance(root, HuffmanLeafNode):
return {root.char: ''}
left_code = HuffmanTree.get_code(root.left)
right_code = HuffmanTree.get_code(root.right)
code = {}
for key, value in left_code.items():
code[key] = '0' + value
for key, value in right_code.items():
code[key] = '1' + value
return code
@staticmethod
def encode(huffmanTree, char: str):
"""
对字符串进行Huffman编码
:param huffmanTree: Huffman树的根节点
:param char: 待编码的字符串
:return: 编码后的bitarray对象
"""
encoding_sets = HuffmanTree.get_code(huffmanTree)
out = bitarray()
for i in char:
out.extend(encoding_sets[i])
return out
@staticmethod
def decode(huffmanTree, encoded_data):
"""
对Huffman编码数据进行解码
:param huffmanTree: Huffman树的根节点
:param encoded_data: 编码数据
:return: 解码后的字符串
"""
root = huffmanTree
decoded_characters = []
i = 0
n = len(encoded_data)
while i < n:
bit = encoded_data[i]
if isinstance(root, HuffmanLeafNode):
decoded_characters.append(root.char)
root = huffmanTree
continue
if bit == 0:
root = root.left
else:
root = root.right
i += 1
else:
if isinstance(root, HuffmanLeafNode):
decoded_characters.append(root.char)
return ''.join(decoded_characters)
使用的示例如下:
s = "hello world!"
data = Counter(s)
# 构建Huffman树
root = HuffmanTree.create_tree(data)
# 序列化
HuffmanTree.save_tree_to_file('encoding_sets', root)
# 反序列化
root = HuffmanTree.load_tree_from_file('encoding_sets')
# 打印编码集
print(HuffmanTree.get_code(root))
# 编码
e = HuffmanTree.encode(root, s)
print(e)
# 编码结果存为二进制文件
with open('test.bin', 'wb') as f:
e.tofile(f)
# 解码
d = HuffmanTree.decode(root, ans)
print(d)
现在我们只需要拥有encoding_sets文件和编码结果,就可以进行解码。同时还起到了一定的加密作用,如果没有encoding_sets,即使拿到编码结果,也不容易获得真实的文本。
哈夫曼编码的实践应用
哈夫曼编码不但能够应用于文本数据的压缩,还能够拓展至其他类型的数据压缩领域,例如图像、音频以及视频文件,其核心在于用更短的编码映射原本出现频率高但编码长度大的数据,例如用8bit表示一个像素,我们可以把出现最频繁的压缩为4bit、3bit甚至更低。