1.微分方程的基本概念
- 含义
微分方程(英语:Differential equation,DE)是一种数学方程,用来描述某一类函数与其导数之间的关系。微分方程的通解是一个符合方程的函数。而在初等数学的代数方程里,解析解是一个具体的值。 (维基百科) - 一般的凡是表示未知函数、未知函数的导数与自变量之间的关系的方程,叫做微分方程。未知函数是一元函数的,叫常微分方程(ODE);未知函数是多元函数的叫做偏微分方程(PDE)。本文只讨论常微分方程。
- 定义式

2.利用dsolve求解微分方程
- 方法简介
启动软件,在命令行窗口运行help dsolve,有如下内容:
dsolve是用来求常微分方程解析解的函数,如果没有给出初始条件或边界条件,则求出通解;如果有,则求出特解。 - 函数格式
S = dsolve('eqn', 'name'); %求通解
% eqn: 微分方程
% name: 自变量名,不写默认为t
S = dsolve('eqn', 'cond', 'name') %求特解
% eqn: 微分方程
% cond: 限制条件
% name: 变量名,不写默认为t
S = dsolve('eqn_1, eqn_2', 'name') %求解微分方程组
% eqn: 微分方程
% cond: 限制条件
% name: 变量名,不写默认为t
- 举例分析
- ex1. 求解下列微分方程的通解:
-
sol: 在命令行窗口运行
dsolve('Dy=4*x^3','x'):

- ex2. 求上题微分方程在y(0)=6时的特解:
sol: 在命令行窗口运行dsolve('Dy=4*x^3',y(0)=6,'x'):

- ex3.求解微分方程组:(题目来源)

sol: 在命令行窗口运行[x y] = dsolve('Dx=y,D2y-y=0','x(0)=2,y(0)=1,Dy(0)=1')

- 注意
- D表示微分符号,Dn表示n阶微分
- 自变量默认为t,其它自变量需要在函数中声明,故例3没有再声明自变量
3.利用ODE求解器求数值解(主要讨论ode45)
- 简介
当难以求得一组微分方程的解析解时,可以利用ode求解器求其数值解,Matlab中求微分方程数值解的函数有七个:ode45,ode23,ode113,ode15s,ode23s,ode23t,ode23tb。这些是Matlab专门用于解微分方程的功能函数。ode求解器有变步长(variable-step)和定步长(fixed-step)两种类型。不同类型有着不同的求解器,其中ode45求解器属于变步长的一种,采用Runge-Kutta算法;其他采用相同算法的变步长求解器还有ode23。 - 函数格式
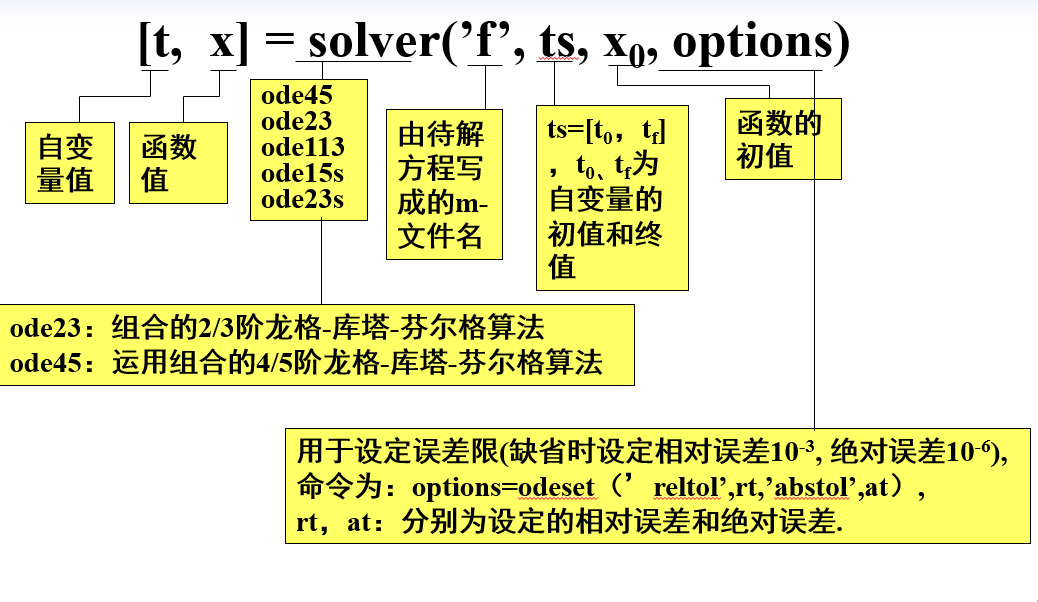
- ode45简介
在命令行窗口运行help ode45:

ode45表示采用四阶-五阶Runge-Kutta算法,它用4阶方法提供候选解,5阶方法控制误差,是一种自适应步长(变步长)的常微分方程数值解法,其整体截断误差为(Δx)^5。解决的是Nonstiff(非刚性)常微分方程。
- 语法
[T,Y] = ode45(odefun,tspan,y0)
[T,Y] = ode45(odefun,tspan,y0,options)
[T,Y,TE,YE,IE] = ode45(odefun,tspan,y0,options)
sol = ode45(odefun,[t0tf],y0...)
[T,Y] = ode45(odefun,tspan,y0)
% odefun: 函数句柄,可以是函数文件名,匿名函数句柄或内联函数名
% tspan: 区间 [t0 tf] 或者一系列散点[t0,t1,...,tf]
% y0: 初始值向量
% T: 返回列向量的时间点
% Y: 返回对应T的求解列向量
% options: 求解参数设置,可以用odeset在计算前设定误差,输出参数,事件等
% TE: 事件发生时间(在设置了事件参数后的对应输出)
% YE: 事件发生时的答案(在设置了事件参数后的对应输出)
% IE: 事件函数消失时的指针(在设置了事件参数后的对应输出)
- 举例分析
- ex1
在[1,4]区间内求解如下微分方程:

sol:将等式变形,求解代码如下:
odefun = @(t,y) (y + 3 *t) / t^2; %定义函数
tspan = [1 4]; %定义求解区间
y0 = -2; %初值
[t,y] = ode45(odefun, tspan, y0);
plot(t,y) %作图
xlabel('t');
ylabel('Dy');
结果如下