面试经典 150 题 - 学习计划 - 力扣（LeetCode）

目录

二叉树

        104. 二叉树的最大深度

        100. 相同的树

        226. 翻转二叉树

        101. 对称二叉树

        105. 从前序与中序遍历序列构造二叉树 

        106. 从中序与后序遍历序列构造二叉树

---

二叉树结构

// Definition for a binary tree node.
struct TreeNode {
     int val;
     TreeNode *left;
     TreeNode *right;
     TreeNode() : val(0), left(nullptr), right(nullptr) {}
     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};

104. 二叉树的最大深度

深度优先搜索（DFS）：时间复杂度：，空间复杂度：

class Solution {
public:
    int maxDepth(TreeNode* root) {
        if (root == nullptr) return 0;
        return max(maxDepth(root->left), maxDepth(root->right)) + 1;
    }
};

广度优先搜索（BFS）：时间复杂度：，空间复杂度：

class Solution {
public:
    int maxDepth(TreeNode* root) {
        if (root == nullptr) return 0;
        queue<TreeNode*> Q;
        Q.push(root);
        int ans = 0;
        while (!Q.empty()) {
            int sz = Q.size();
            while (sz > 0) {
                TreeNode* node = Q.front();Q.pop();
                if (node->left) Q.push(node->left);
                if (node->right) Q.push(node->right);
                sz -= 1;
            }
            ans += 1;
        } 
        return ans;
    }
};

100. 相同的树

采用深度优先搜索，递归判断每个节点是否相等，最终判断是不是相同的树。

class Solution {
public:
    bool isSameTree(TreeNode* p, TreeNode* q) {
        if (p == nullptr && q == nullptr) {
            return true;
        } else if (p == nullptr || q == nullptr) {
            return false;
        } else if (p->val != q->val) {
            return false;
        } else {
            return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
        }
    }
};

226. 翻转二叉树

深度优先搜索，从根节点开始，递归地对树进行遍历，从叶子节点开始翻转，最后root节点左右子树翻转。

class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        if (root == nullptr) {
            return nullptr;
        }
        TreeNode* left = invertTree(root->left);
        TreeNode* right = invertTree(root->right);
        root->left = right;
        root->right = left;
        return root;
    }
};

101. 对称二叉树

简单的想法就是借助翻转二叉树和相同的树来判断，即root节点的左子树进行翻转(当然也可以整棵树进行翻转)，和root节点的右子树判断是否是相同的树，如果相同即为对称二叉树。

class Solution {
public:
    bool isSymmetric(TreeNode* root) {
        root->left = invertTree(root->left);
        return isSameTree(root->left, root->right);
    }
};

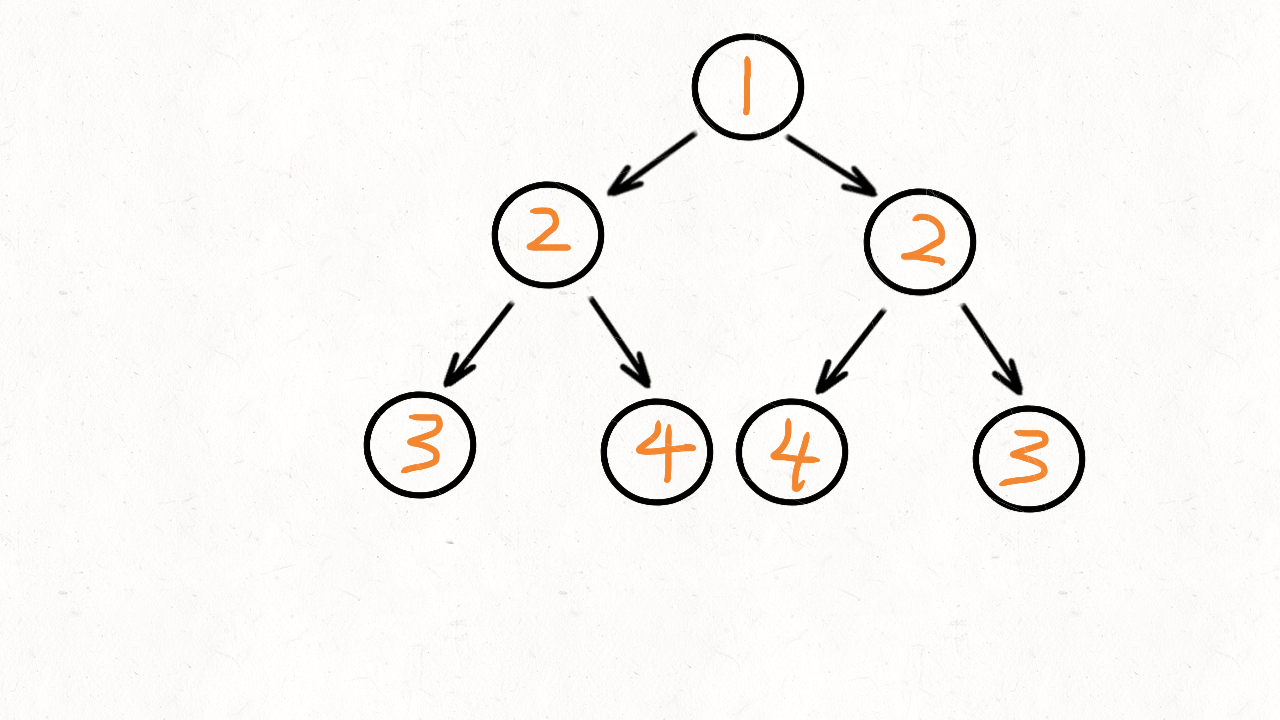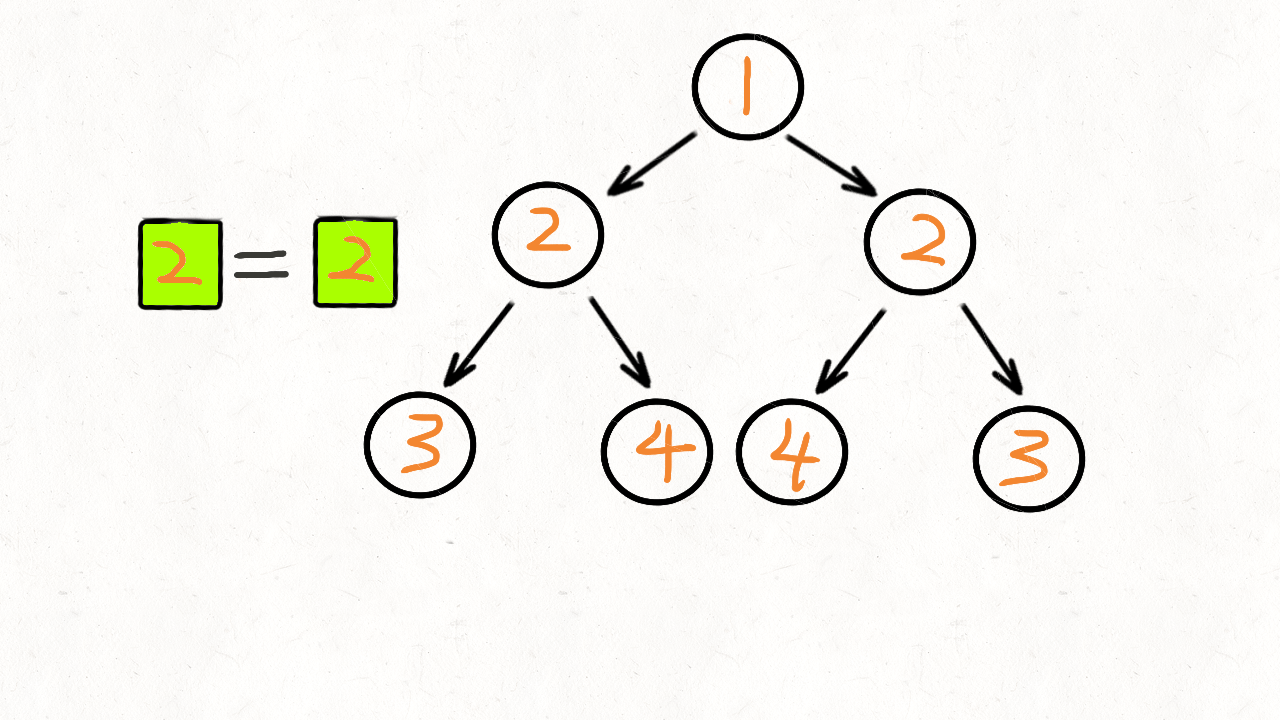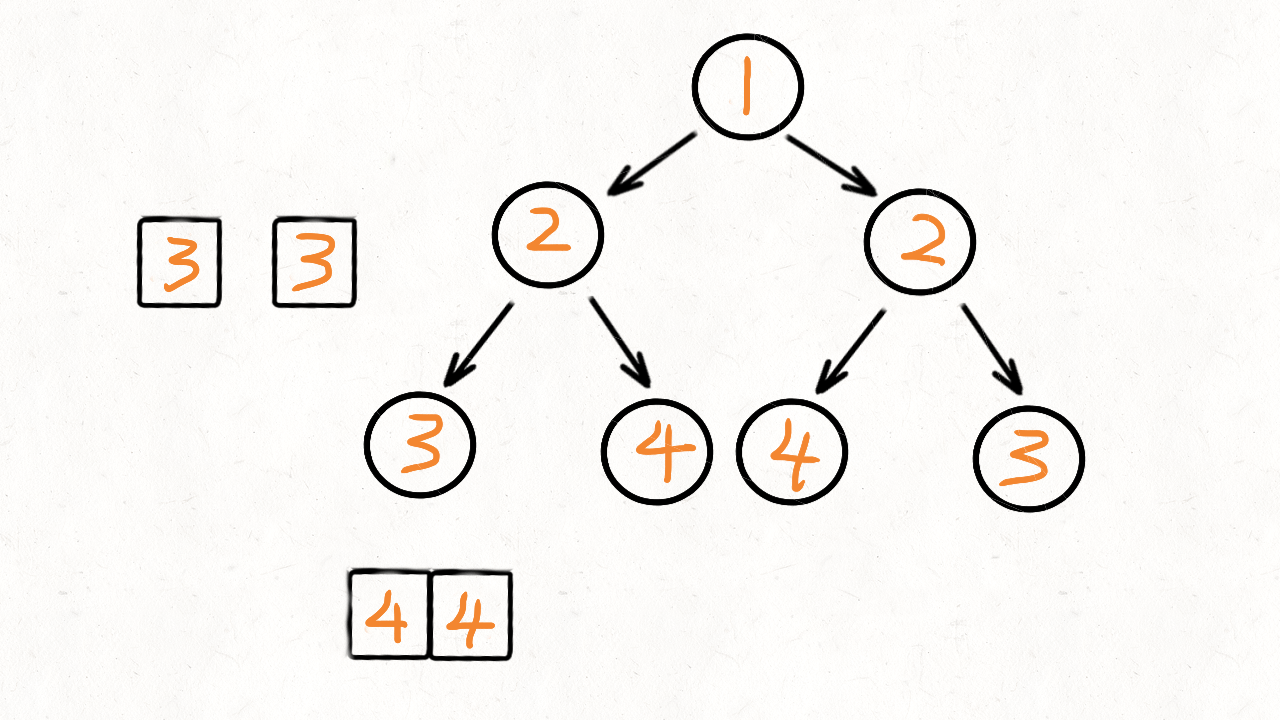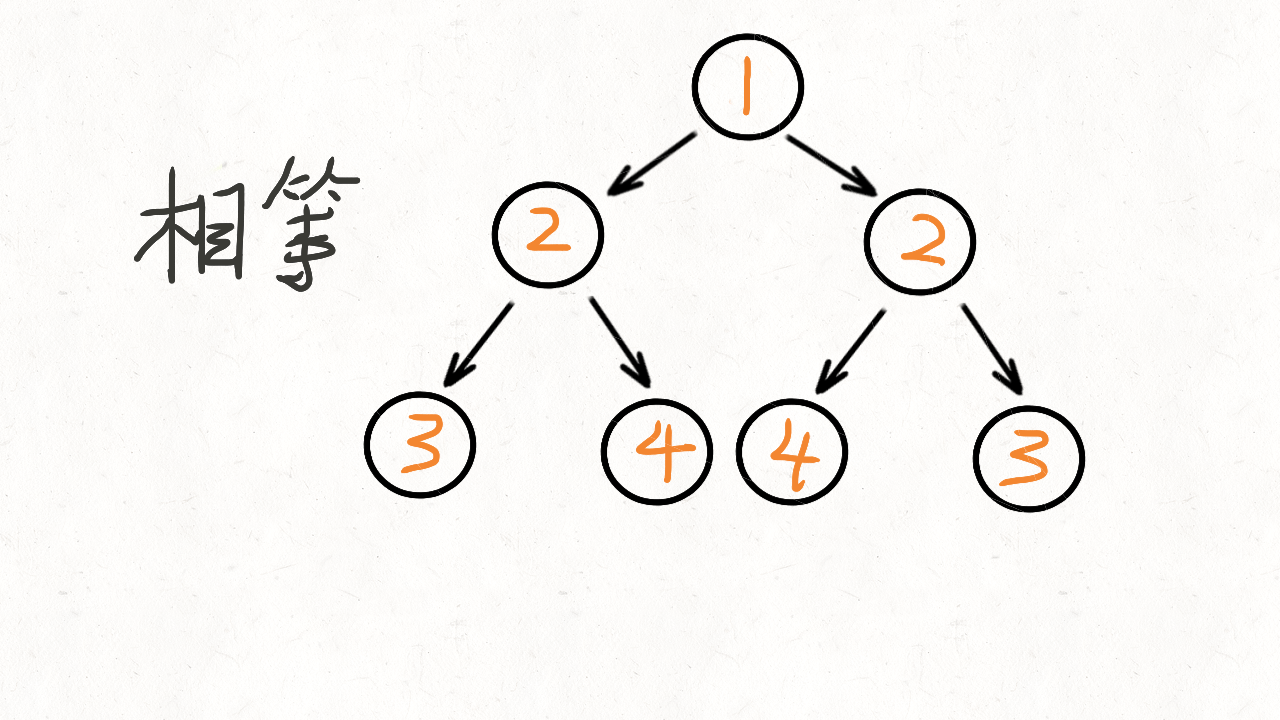
 那如何一次遍历解决?

• 它们的两个根结点具有相同的值
• 每个树的右子树都与另一个树的左子树镜像对称

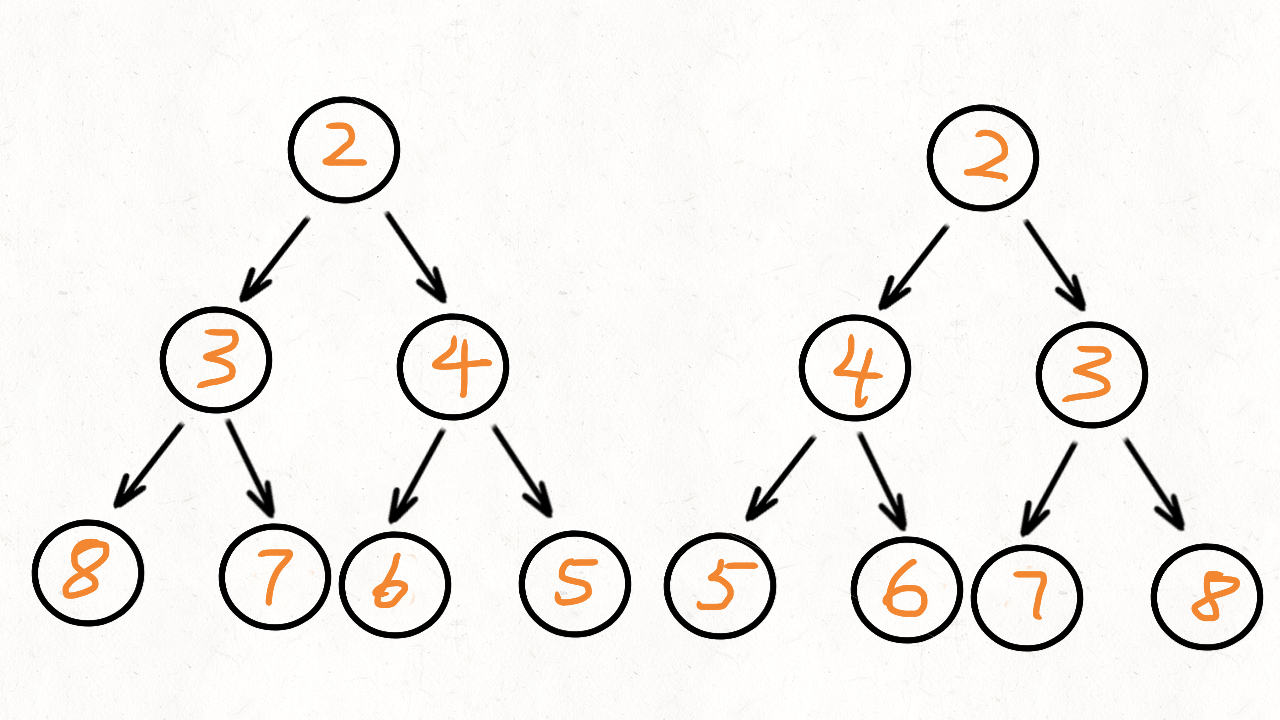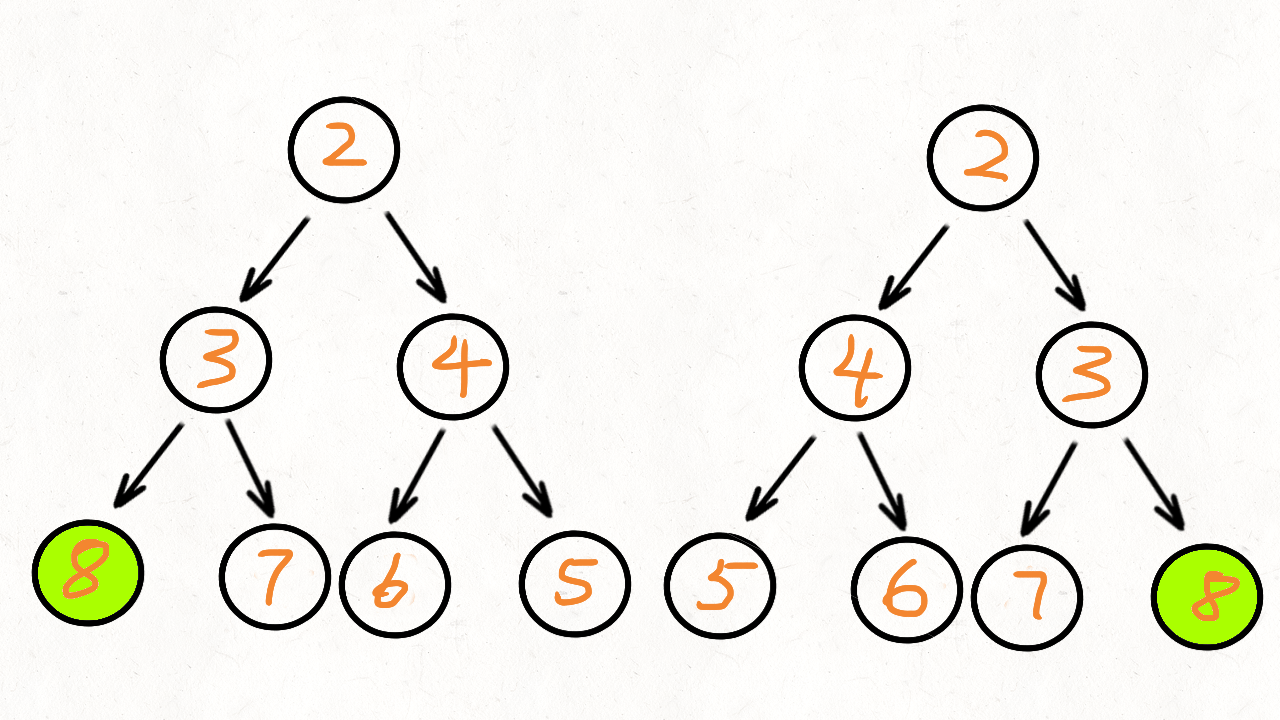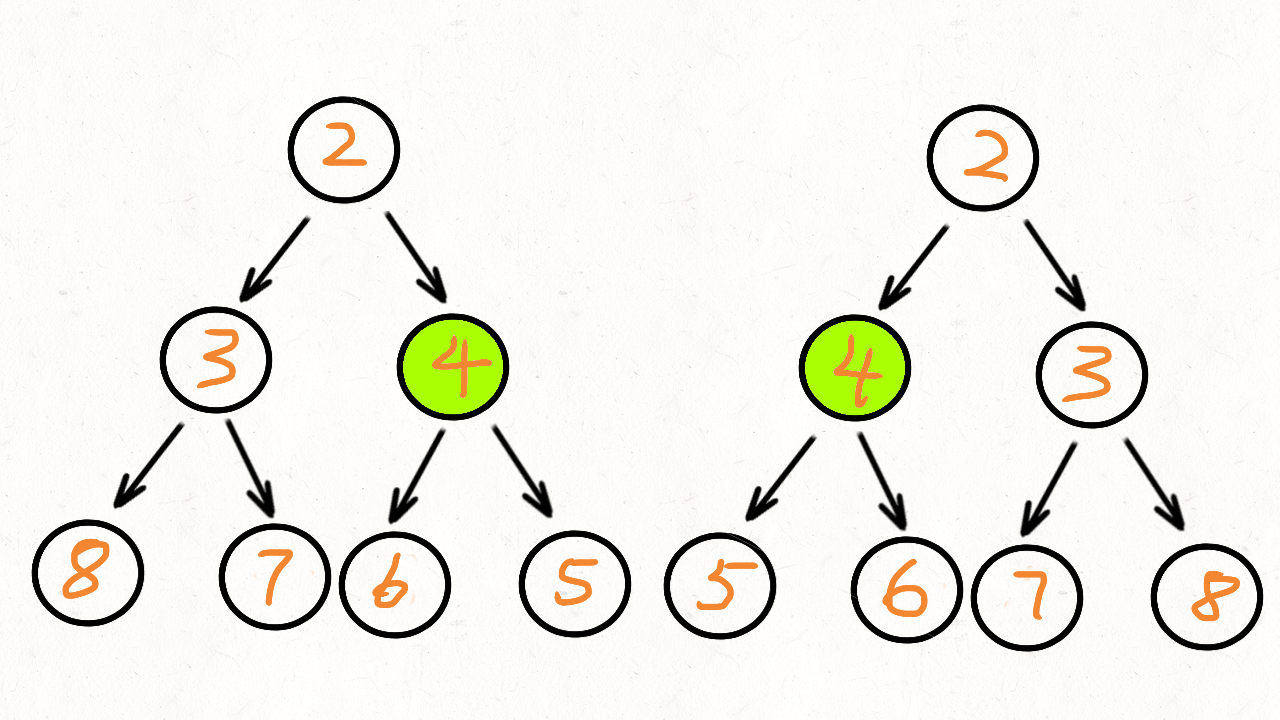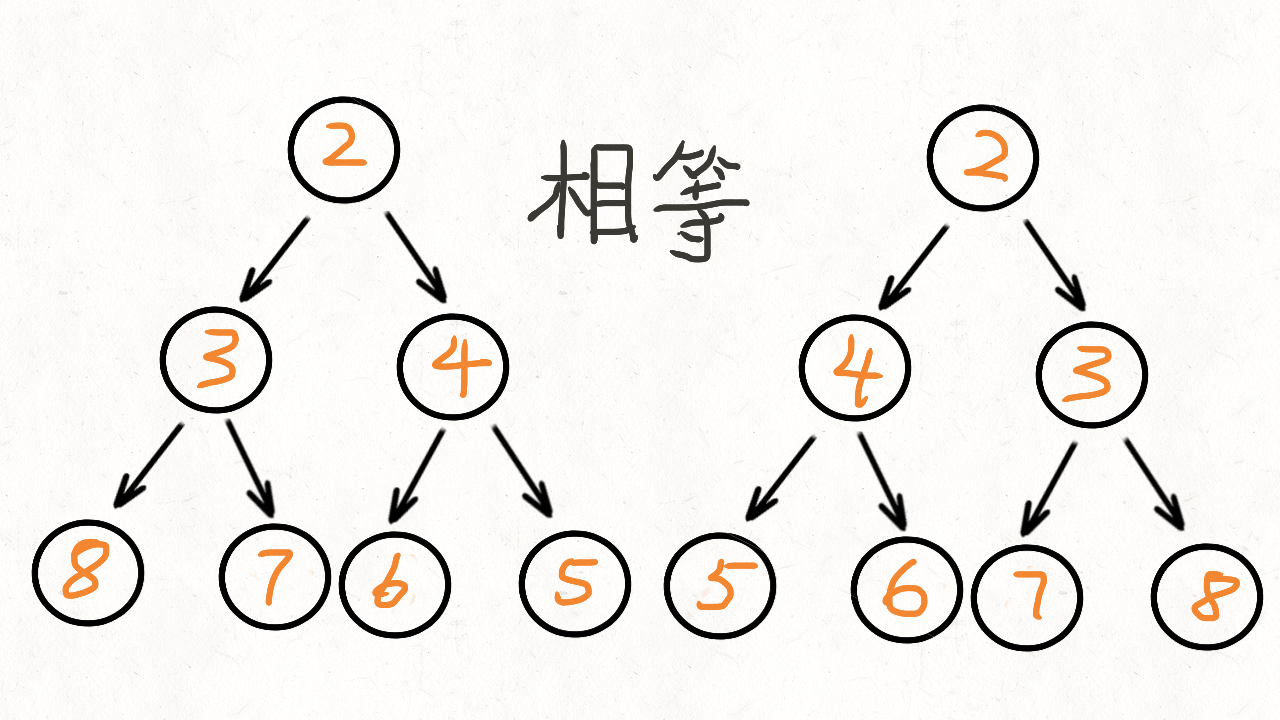
class Solution {
public:
    bool check(TreeNode *p, TreeNode *q) {
        if (!p && !q) return true;
        if (!p || !q) return false;
        return p->val == q->val && check(p->left, q->right) && check(p->right, q->left);
    }

    bool isSymmetric(TreeNode* root) {
        return check(root, root);
    }
};

当然还可以用迭代的方法，改用队列来实现。

105. 从前序与中序遍历序列构造二叉树

二叉树前序遍历的顺序为：先遍历根节点；随后递归地遍历左子树；最后递归地遍历右子树。

二叉树中序遍历的顺序为：先递归地遍历左子树；随后遍历根节点；最后递归地遍历右子树。

class Solution {
private:
    unordered_map<int, int> dic;

public:
    TreeNode* myBuildTree(const vector<int>& preorder, int preorder_left, int preorder_right, int inorder_left, int inorder_right) {
        if (preorder_left > preorder_right) {
            return nullptr;
        }
        
        // 前序遍历中的第一个节点就是根节点
        int preorder_root = preorder_left;
        // 在中序遍历中定位根节点
        int inorder_root = dic[preorder[preorder_root]];
        
        // 先把根节点建立出来
        TreeNode* root = new TreeNode(preorder[preorder_root]);
        // 得到左子树中的节点数目
        int size_left_subtree = inorder_root - inorder_left;
        // 递归地构造左子树，并连接到根节点
        // 先序遍历中「从 左边界+1 开始的 size_left_subtree」个元素就对应了中序遍历中「从 左边界 开始到 根节点定位-1」的元素
        root->left = myBuildTree(preorder, preorder_left + 1, preorder_left + size_left_subtree, inorder_left, inorder_root - 1);
        // 递归地构造右子树，并连接到根节点
        // 先序遍历中「从 左边界+1+左子树节点数目 开始到 右边界」的元素就对应了中序遍历中「从 根节点定位+1 到 右边界」的元素
        root->right = myBuildTree(preorder, preorder_left + size_left_subtree + 1, preorder_right, inorder_root + 1, inorder_right);
        return root;
    }

    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        int n = preorder.size();
        // 构造哈希映射，帮助我们快速定位根节点
        for (int i = 0; i < n; ++i) {
            dic[inorder[i]] = i;
        }
        return myBuildTree(preorder, 0, n - 1, 0, n - 1);
    }
};

106. 从中序与后序遍历序列构造二叉树

二叉树中序遍历的顺序为：先递归地遍历左子树；随后遍历根节点；最后递归地遍历右子树。

二叉树后序遍历的顺序为：先递归地遍历左子树；随后递归地遍历右子树；最后遍历根节点。

class Solution {
    int post_idx;
    unordered_map<int, int> idx_map;
public:
    TreeNode* mybuildTree(int in_left, int in_right, vector<int>& postorder){
        // 如果这里没有节点构造二叉树了，就结束
        if (in_left > in_right) {
            return nullptr;
        }

        // 选择 post_idx 位置的元素作为当前子树根节点
        int root_val = postorder[post_idx];
        TreeNode* root = new TreeNode(root_val);

        // 根据 root 所在位置分成左右两棵子树
        int index = idx_map[root_val];

        // 下标减一
        post_idx--;
        // 构造右子树
        root->right = mybuildTree(index + 1, in_right, postorder);
        // 构造左子树
        root->left = mybuildTree(in_left, index - 1, postorder);
        return root;
    }

    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
        // 从后序遍历的最后一个元素开始
        post_idx = (int)postorder.size() - 1;

        // 建立（元素，下标）键值对的哈希表
        int idx = 0;
        for (auto& val : inorder) {
            idx_map[val] = idx++;
        }
        return mybuildTree(0, (int)inorder.size() - 1, postorder);
    }
};