数据结构基础详解(C语言): 栈与队列的详解附完整代码

数据结构栈

栈的核心重点：

栈是只能从表尾插入和删除的数据结构。
栈的顺序存储结构由两部分组成，top指针和数组。
链栈其实本质就是单链表头插法

文章目录

数据结构栈
1.栈的基本概念
- 1.1 栈的常用操作
2.栈的存储结构
- 2.1 栈的顺序存储结构
- - 2.1.1 栈的定义
  - 2.1.2 栈的初始化
  - 2.1.3 入栈
  - 2.1.4 出栈
  - 2.1.5 读取栈顶元素
  - 2.1.6 共享栈
- 2.2 栈的链式存储结构
- - 2.2.1 链栈的定义
  - 2.2.2 链栈的初始化
  - 2.2.3 入栈
  - 2.2.4 出栈
  - 2.2.5 取栈顶元素
  - 2.2.6 销毁栈
队列
1.队列的定义
1.1 队列的基本操作
2.队列的实现
- 2.1 顺序存储的实现
- - 2.1.1 队列的定义
  - 2.1.2 队列的初始化
  - 2.1.3 队列判空
  - 2.1.4 入队和出队
  - 2.1.5 取队头元素
  - 2.1.6 判断队列已满/为空的其他两种方案
- 2.2 链式存储的实现
- - 2.2.1 定义
  - 2.2.2 初始化
  - 2.2.3 判空与判满
  - 2.2.4 入队
  - 2.2.5 出队

1.栈的基本概念

栈( Stack）是只允许在一端进行插入或删除操作的线性表
在这里插入图片描述

1.1 栈的常用操作

InitStack(&s):初始化栈,构造一个空栈S,分配内存空间.
DestroyStack(&L):销毁栈.销毁并释放S所占用的内存空间
Push(&S,x):进栈,若栈S未满,则将x加入使之成为新栈顶
Pop(&S,&x):出栈,若栈S非空,则弹出栈顶元素,并用x放回
GetTop(S,&x):读栈顶元素.若栈S非空,则用x返回栈顶元素
StackEmpty(S):判断一个栈S是否为空.若S为空,则返回true,否则返回false

2.栈的存储结构

2.1 栈的顺序存储结构

2.1.1 栈的定义

#define MaxSize 10
typedef struct{
	int data[MaxSize]; //静态数组存放栈中元素 
	int top;           // 栈顶元素 
}SqStack;

2.1.2 栈的初始化

void InitStack(SqStack &S){
	S.top=-1;   //初始化栈顶指针 
}

2.1.3 入栈

bool Push(SqStack &S,int x)
{
	if(S.top==MaxSize-1)
		return false;
	S.top=S.top+1;
	S.data[S.top]=x;
	return true;
}

2.1.4 出栈

bool Pop(SqStack &S,int &x)
{
	if(S.top==-1)   //栈空,报错 
		return false;
	x=S.data[S.top];  //栈顶元素先出栈 
	S.top=S.top-1; //指针再减1 
	return true;
}

2.1.5 读取栈顶元素

bool GetTop(SqStack &S,int &x){
	if(S.top==-1)
		return false;
	x=S.data[S.top];
	return true;
}

int main()
{	
	SqStack S;
	InitStack(S);
	int x=0;
	Push(S,2);
	Push(S,3);
	Push(S,4);
	GetTop(S,x);
	printf("%d",x);
}

上述完整代码如下:

#include <stdio.h>
#include <stdlib.h>

#define MaxSize 10
typedef struct{
	int data[MaxSize]; //静态数组存放栈中元素 
	int top;           // 栈顶元素 
}SqStack;

void InitStack(SqStack &S){
	S.top=-1;   //初始化栈顶指针 
}

bool Push(SqStack &S,int x)
{
	if(S.top==MaxSize-1)
		return false;
	S.top=S.top+1;
	S.data[S.top]=x;
	return true;
}

bool Pop(SqStack &S,int &x)
{
	if(S.top==-1)   //栈空,报错 
		return false;
	x=S.data[S.top];  //栈顶元素先出栈 
	S.top=S.top-1; //指针再减1 
	return true;
}
bool GetTop(SqStack &S,int &x){
	if(S.top==-1)
		return false;
	x=S.data[S.top];
	return true;
} 


int main()
{	
	SqStack S;
	InitStack(S);
	int x=0;
	Push(S,2);
	Push(S,3);
	Push(S,4);
	GetTop(S,x);
	printf("%d",x);
}

2.1.6 共享栈

两个栈共享同一片空间

#define MaxSize 10
typedef struct{
	int data[MaxSize]; //静态数组存放栈中元素 
	int top0;           // 0号栈顶元素
	int top1;           // 1号栈顶元素
}ShStack;

void InitStack(ShStack &S){
s.top0=-1;  //初始化栈顶指针
s.top1=MaxSize;

2.2 栈的链式存储结构

使用不带头结点的链表

2.2.1 链栈的定义

typedef struct LinkNode{
    int data;//数据域
    struct LinkNode *next;//指针域 
}stackNode,*LinkStack;

2.2.2 链栈的初始化

void InitStack(LinkStack &s)
{
	s=NULL;//不需要头节点 
}

2.2.3 入栈

bool Push(LinkStack &S,int e)       
{
	stackNode *p=(stackNode *)malloc(sizeof(stackNode));
	p->data=e;
	p->next=NULL;
	if(S==NULL)
	{
		S=p;
	}
	else
	{
		p->next=S;
		S=p;
	}
	return true;
}

2.2.4 出栈

bool Pop(LinkStack &S,int &e)
{
	stackNode *p;
	if(S==NULL)
		return false;
	else
	{
		p=S;
		e=p->data;
		S=S->next;
		delete p;
		return true;
	}
}

2.2.5 取栈顶元素

int top(LinkStack s)
{
	if(s==NULL)
		return -1;
	return s->data;
}

2.2.6 销毁栈

bool DestoryStack(LinkStack &S)
{
	stackNode *p;
	while(S)
	{
		p=S;
		S=S->next;
		delete p;
	}
	S=NULL;
	return true;
}

队列

队列的核心:队列是一种先进先出的数据结构。
顺序存储是一个front指针和一个rear指针，和数组
front指针指向队头，rear指针指向队尾。
队空条件：Q.front==Q.rear
进队：Q.data[Q.rear++]
出队：Q.data[Q.front++]

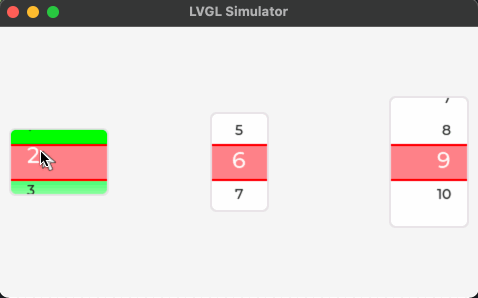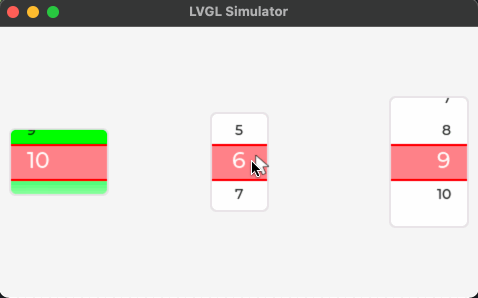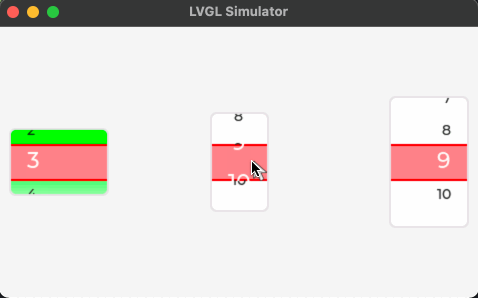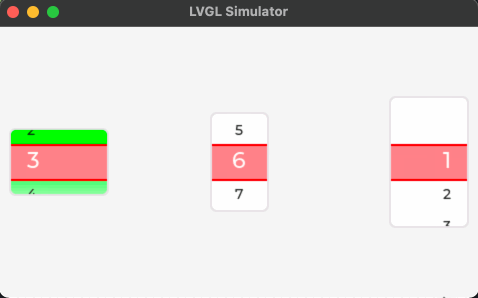
快速图解复习队列:
在这里插入图片描述

在这里插入图片描述

1.队列的定义

队列( Queue）是只允许在一端进行插入，在另一端删除的线性表
在这里插入图片描述

1.1 队列的基本操作

InitQueue(&Q):初始化队列，构造一个空队列Q。
DestroyQueue(&Q):销毁队列。销毁并释放队列Q所占用的内存空间
EnQueue(&Q):入队，若队列Q未满，将x加入，使之成为新的队尾
DeQueue(&Q,&x):出队，若队列Q非空，删除队头元素，并用x返回
GetHead(Q,&x):读队头元素，若队列Q非空，则将队头元素赋值给x。
QueueEmpty(Q):判队列空，若队列Q为空返回true，否则返回false。

2.队列的实现

2.1 顺序存储的实现

在接下来的代码实现中,rear和front指针最初指向相同的位置,在实际的题目中,我们也可以让rear指向data[1],front指向data[0],不必拘泥于某种固定的格式.
在这里插入图片描述

2.1.1 队列的定义

用静态数组存放数据元素
声明一个队头和队尾指针
有typedef,所以定义typedef struct后面没加SqQueue,这个就是一个可写可不写的方式,因为我们取好了别名,也不用struct SqQueue sq1; 这种形式去定义队列

typedef struct{
    int data[MaxSize];
    int front,rear;
}SqQueue;

2.1.2 队列的初始化

void InitQueue(SqQueue &Q)
{
	Q.front=Q.rear=0;
}

2.1.3 队列判空

bool QueueEmpty(SqQueue &Q)
{
	if(Q.front==Q.rear)
	 	return true;
	return false;
}

2.1.4 入队和出队

入队和出队要注意队列是循环的,出到最后之后,重新找头部从头部开始出队,以此类推
当然了,简单的问题中可能不使用这种循环队列的形式.

在这里插入图片描述
值得思考的是,在入队和出队操作过程中,我们需要进行判断队列是否为空或者队列是否满的,下面先采取放弃一个存储空间的方式,进行判满操作,通过放弃一个存储空间,就不会和判空操作相同,即rear指向最后一个空间没存的情况下就判断它已经满了

⭐️入队

bool EnQueue(SqQueue &Q,int x)
{
	if((Q.rear+1)%MaxSize==Q.front)
	 	return false;
	Q.data[Q.rear]=x;
	Q.rear=(Q.rear+1)%MaxSize;
	return true;
}

⭐️出队

bool DeQueue(SqQueue &Q,int &x)
{
	if(Q.rear==Q.front)
	 	return false;
	x=Q.data[Q.front];
	Q.front=(Q.front+1)%MaxSize;
	return true;
}

当前实现队列元素的个数=(rear+MaxSize-front)%MaxSize

2.1.5 取队头元素

bool GetHead(SqQueue Q,int &x)
{
	if(Q.rear==Q.front)
	 	return false;
	x=Q.data[Q.front];
	return true;
}

上述完整代码:

#include <stdio.h>
#include <stdlib.h>
#define  MaxSize 10
typedef struct{
    int data[MaxSize];
    int front,rear;
}SqQueue;

void InitQueue(SqQueue &Q)
{
	Q.front=Q.rear=0;
}

bool QueueEmpty(SqQueue &Q)
{
	if(Q.front==Q.rear)
	 	return true;
	return false;
}

bool EnQueue(SqQueue &Q,int x)
{
	if((Q.rear+1)%MaxSize==Q.front)
	 	return false;
	Q.data[Q.rear]=x;
	Q.rear=(Q.rear+1)%MaxSize;
	return true;
}

bool DeQueue(SqQueue &Q,int &x)
{
	if(Q.rear==Q.front)
	 	return false;
	x=Q.data[Q.front];
	Q.front=(Q.front+1)%MaxSize;
	return true;
}

bool GetHead(SqQueue Q,int &x)
{
	if(Q.rear==Q.front)
	 	return false;
	x=Q.data[Q.front];
	return true;
}

int main()
{
	SqQueue q;
}

2.1.6 判断队列已满/为空的其他两种方案

之前我们的方案是牺牲一个存储空间
方案一:增加一个size数据,记录队列的当前长度

typedef struct{
    int data[MaxSize];
    int front,rear;
    int size;
}SqQueue;

size==MaxSize //队列已满
size==0       //队列为空

方案二:增加一个tag数据,指明最近的依次操作是删除还是插入

typedef struct{
    int data[MaxSize];
    int front,rear;
    int tag;  //tag=1 代表上一次是插入 tag=0代表上一次是删除
}SqQueue;

rear==front&&tag=1   //队列已满
rear==front&&tag=0   //队列为空

2.2 链式存储的实现

2.2.1 定义

定义一个结构体是链式队列结点
再定义一个结构体,里面有2个结点指针指向结点,这样便于代码的简洁

typedef struct LinkNode{
    int data;
    LinkNode *next;
}LinkNode;

typedef struct {
    LinkNode *front,*rear;
}LinkQueue;

2.2.2 初始化

void InitQueue(LinkQueue &Q)
{
	Q.front=Q.rear=(LinkNode*)malloc(sizeof(LinkNode));
	Q.front->next=NULL;
}

2.2.3 判空与判满

判空

bool QueueEmpty(LinkQueue Q)
{
	if(Q.front==Q.rear)
	 	return true;
	return false;
}

链式存储一般情况不会满,所以不判满

2.2.4 入队

⭐️不带头结点的入队

bool EnQueue(LinkQueue &Q,int x)
{
	LinkNode *s=(LinkNode*)malloc(sizeof(LinkNode));
	s->data=x;
	s->next=NULL;
	Q.rear->next=s;
	Q.rear=s;
	return true;
}

⭐️带头结点的入队第一个元素要特殊处理

bool EnQueue(LinkQueue &Q,int x)
{
	LinkNode *s=(LinkNode*)malloc(sizeof(LinkNode));
	s->data=x;
	s->next=NULL;
	if(Q.front==NULL)
	{
		Q.front=s;
		Q.rear=s;
	}
	else
	{
		Q.rear->next=s;
		Q.rear=s;
	}
	return true;
}

2.2.5 出队

出队的操作,值得注意的是,如果front指向的是最后一个元素,将他出队后 front指针就指向空了,但是此时的rear指针被蒙在鼓里,所以如果此时p指针和rear指针相同,则说明rear要更新和front指针一样,如果不更新,rear还指向最后一个元素

为什么只有指向最后一个元素的情况下才更新呢?
因为其实,不到最后一个出队,rear和front之间没什么关系,没什么联系

⭐️不带头结点的出队

bool DeQueue(LinkQueue &Q,int &x)  //不带头结点 
{
	if(Q.front==NULL)
	 	return false;
	LinkNode *p=Q.front; 
	x=p->data;
	Q.front=p->next;
	if(Q.rear==p)
	{
		Q.rear=Q.front; //王道给出的是Q.front==NULL 和 Q.rear==NULL 我觉得没必要,这么写就行 
	}
	free(p);
	return true;
}

⭐️带头结点的出队

bool DeQueue(LinkQueue &Q,int &x)  //带头结点 
{
	if(Q.rear==Q.front)
	 	return false;
	LinkNode *p=Q.front->next; 
	x=p->data;
	Q.front->next=p->next;
	if(Q.rear==p)
	{
		Q.rear=Q.front;
	}
	free(p);
	return true;
}