探索数据结构：跳表的分析与实现

news2024/11/15 2:07:05


✨✨ 欢迎大家来到贝蒂大讲堂✨✨

🎈🎈养成好习惯，先赞后看哦~🎈🎈

所属专栏：数据结构与算法
贝蒂的主页：Betty’s blog

1. 跳表的概念

**跳表(Skiplist)**是在有序链表基础上增加了“跳跃”功能的一种数据结构。它在原来的有序链表上添加多级索引，以实现通过索引快速查找，能够支持快速的删除、插入和查找操作。实际上，跳表是一种增加了前向指针的链表，属于随机化的数据结构。
跳表本质上是一种查找结构，可作为key或者key/value的查找模型，与平衡搜索树和哈希表的价值一样，用于解决算法中的查找问题。跳表由William Pugh发明，最早出现于他在1990年发表的论文《Skip Lists: A Probabilistic Alternative to Balanced Trees》，对细节感兴趣的同学可以下载论文原文阅读。

2. 跳表的思路

2.1 提出问题

跳表最开始的思路如下：

  1. William Pugh最初的想法是在有序链表中，每相邻两个节点升高一层，增加一个指针指向下下个节点，这样所有新增加的指针连成新的链表，且此链表包含的节点个数是原来的一半，如图b。
  2. 以此类推，可在第二层新产生的链表上继续为每相邻两个节点升高一层增加指针，产生第三层链表，这样搜索效率进一步提高，如图c。

按照上面生成链表的方式，上面每一层链表的节点个数，是下面一层的节点个数的一半，这样查找过程就非常类似二分查找，使得查找的时间复杂度可以从原本链表的 O ( N ) O(N) O(N)降低到 O ( l o g N ) O(logN) O(logN)。

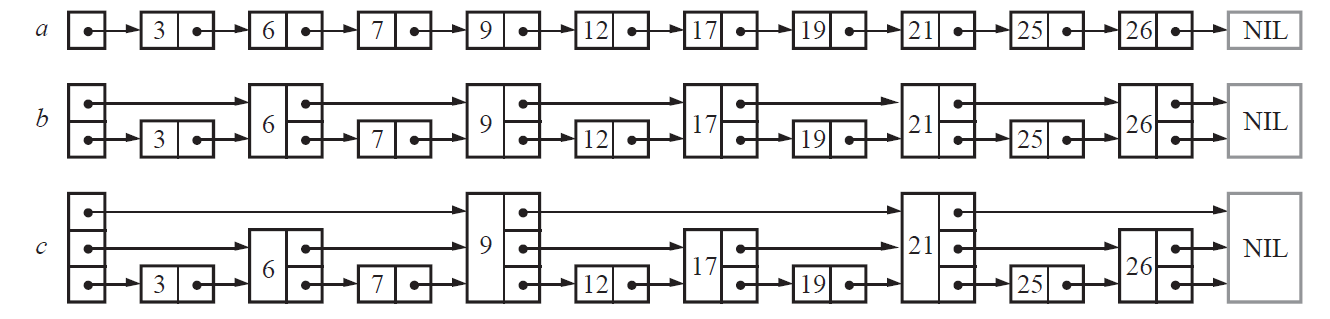
image.png
但是很快，William Pugh就发现这个结构在插入删除数据的时候有很大的问题，插入或者删除一个节点之后，就会打乱上下相邻两层链表上节点个数严格的2:1的对应关系。如果要维持这种对应关系，就必须把新插入的节点后面的所有节点（也包括新插入的节点）重新进行调整，这会让时间复杂度重新劣为成 O ( N ) O(N) O(N)。

2.2 解决方法

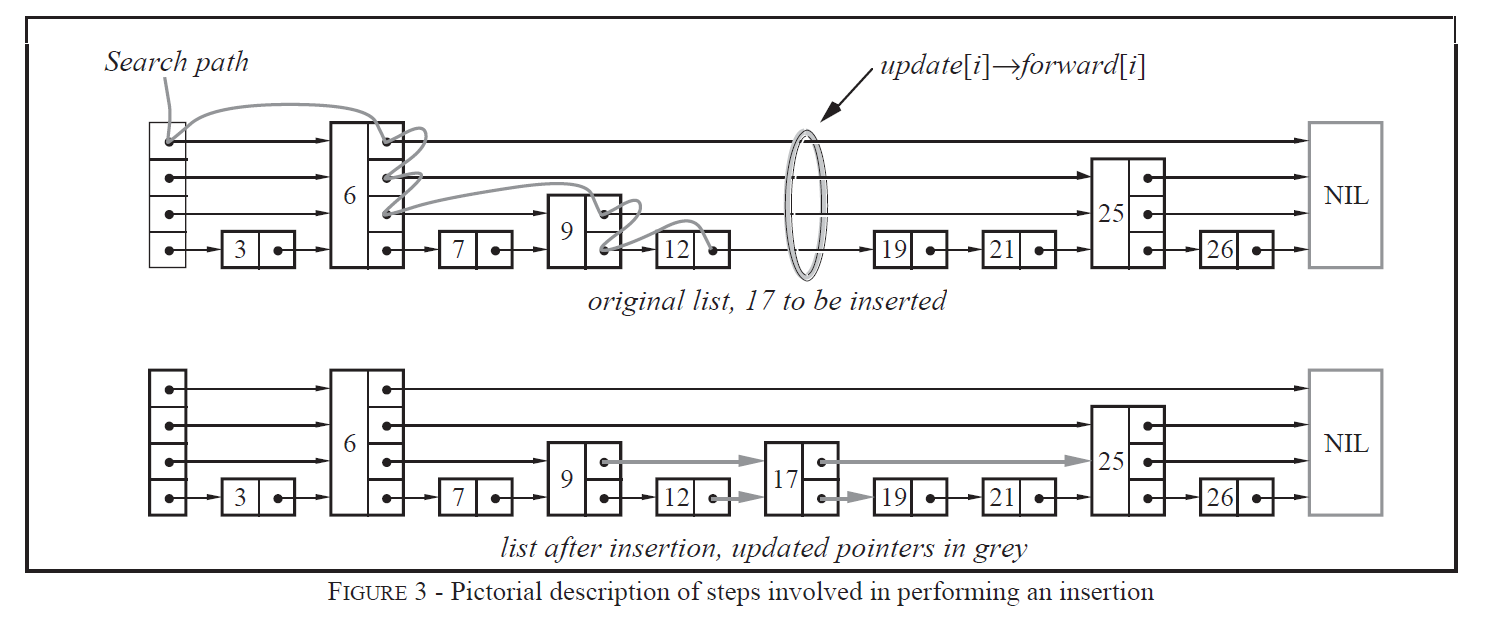
skiplist的设计为了避免这种问题，做了一个大胆的处理，不再严格要求对应比例关系，而是插入一个节点的时候随机出一个层数。这样每次插入和删除都不需要考虑其他节点的层数，这样就好处理多了。细节过程入下图：
image.png

3. 随机函数的设计

为了保证我们skiplist的效率，所以随机层数时一定要合理——保证层数越高的出现概率越小。William Pugh设计的伪代码如下：
image.png
在Redis中的skiplist实现中，这两个参数的取值为：

  • p = 1/4
  • MarxLevel = 32

根据前面randomLevel()的伪码，我们可以分析每一层的概率分布：

  1. 节点层数恰好等于1的概率为1 - p。
  2. 节点层数大于等于2的概率为p，而节点层数恰好等于2的概率为p(1 - p)。
  3. 节点层数大于等于3的概率为p²，而节点层数恰好等于3的概率为p²(1 - p)。
  4. 节点层数大于等于4的概率为p³，而节点层数恰好等于4的概率为p³(1 - p)。

……

然后我们可以计算一个节点的平均层数，计算如下：
KaTeX parse error: {align*} can be used only in display mode.
现在很容易计算出：

  • 当p=1/2时，每个节点所包含的平均指针数目为2；
  • 当p=1/4时，每个节点所包含的平均指针数目为1.33。

4. 实现跳表

4.1 跳表的结构

为了适合所有类型，我们同样采用泛型编程的方式。其中跳表节点应该包含键值_val以及下几个节点的索引_nextV。而跳表中则需要包含三个成员变量：_head(头节点)，_maxLevel(最大层数)，_p(生成概率)。

template<class T>
//跳表节点
struct SkipListNode
{
	T _val;
	vector<SkipListNode*> _nextV;
	SkipListNode(const T& val,int level)
		:_val(val)
		,_nextV(level,nullptr)
	{}
};
//跳表
template<class T>
class SkipList
{
	typedef SkipListNode<T> Node;
public:
	SkipList();
	bool Search(int target);
	void Add(int num);
	bool Erase(int num);
    // 析构函数
    ~SkipList();
private:
	Node* _head;
	size_t _maxLevel = 32;
	double _p = 0.25;
};

4.2 跳表的初始化为销毁

跳表的初始化只需要生成一个头结点，顺便播下随机种子即可。

SkipList()
{
    srand((unsigned int)time(NULL));
    _head = new Node(T(), 1);//初始化一个头节点
}

跳表的销毁和链表的销毁差不多，直接遍历销毁即可。

// 析构函数
~SkipList()
{
    Node* cur = _head;
    while (cur)
    {
        //保存下一个节点
        Node* next = cur->_nextV[0];
        delete cur;
        cur = next;
    }
}

4.3 跳表的查找

跳表的查找就是从最高层开始遍历，如果查找值比下一个索引节点的值要大，那么往右继续查找；如果查找值比下一个索引节点的值要小或者为空，则往下继续查找，最后如果找到节点返回true，否则返回false。

bool Search(int target)
{
    Node* cur = _head;
    //从最高层开始筛选
    int level = _head->_nextV.size() - 1;
    while (level >= 0)
    {
        //大于往右走
        if (cur->_nextV[level] && target > cur->_nextV[level]->_val)
        {
            cur = cur->_nextV[level];
        }
        //为空或者小于等于往下走
        else if (cur->_nextV[level] == nullptr || target < cur->_nextV[level]->_val)
        {
            --level;
        }
        //相当返回true
        else
        {
            return true;
        }
    }
    return false;
}

4.4 跳表的插入

跳表的插入逻辑稍微有点复杂，需要先找到插入位置的前驱节点集合，然后再实现链接。并且还需要实现一个随机函数，生成随机层数，如果层数比原来层数都大则需要更新层数。

//寻找前驱节点集合
vector<Node*> FindPrevNode(int num)
{
    Node* cur = _head;
    //从最高层开始筛选
    int level = _head->_nextV.size() - 1;
    vector<Node*> preV(level + 1, nullptr);
    while (level >= 0)
    {
        //大于往右走
        if (cur->_nextV[level] && num > cur->_nextV[level]->_val)
        {
            cur = cur->_nextV[level];
        }
        //为空或者小于等于往下走
        else if (cur->_nextV[level] == nullptr || num <= cur->_nextV[level]->_val)
        {
            preV[level--] = cur;
        }
    }
    return preV;
}
//生成随机层数
int RandomLevel()
{
    size_t level = 1;

    // rand() / RAND_MAX -> [0, 1]
    while (rand() <= RAND_MAX * _p && level <= _maxLevel)
    {
        level++;
    }
    return level;
}
void Add(int num)
{
    //寻找前驱节点
    vector<Node*> preV = FindPrevNode(num);
    //随机层数
    int level = RandomLevel();
    Node* newnode = new Node(num, level);
    //如果超过最大层数
    if (level > _head->_nextV.size())
    {
        _head->_nextV.resize(level, nullptr);
        preV.resize(level, _head);
    }
    //链接前后节点
    for (int i = 0; i < level; i++)
    {
        newnode->_nextV[i] = preV[i]->_nextV[i];
        preV[i]->_nextV[i] = newnode;
    }
}

4.5 跳表的删除

跳表的删除逻辑同样需要先找到该节点的前驱节点集合，然后重新链接后删除，如果删除的节点层数最高的话，最后还可以判断是否需要减少层数。

bool Erase(int num)
{
    vector<Node*> preV = FindPrevNode(num);
    // 第一层下一个不是val，则val不在跳表中
    if (preV[0]->_nextV[0] == nullptr || preV[0]->_nextV[0]->_val != num)
    {
        return false;
    }
    //删除节点
    Node* del = preV[0]->_nextV[0];

    // del结点每一层前后指针链接起来
    for (size_t i = 0; i < del->_nextV.size(); i++)
    {
        preV[i]->_nextV[i] = del->_nextV[i];
    }
    delete del;

    // 如果删除最高层结点，把头节点的层数也降一下
    int i = _head->_nextV.size() - 1;
    while (i >= 0)
    {
        //直接为空
        if (!_head->_nextV[i])
        {
            i--;
        }
        else
        {
            break;
        }
    }
    //调整
    _head->_nextV.resize(i + 1);
    return true;
}

5. 复杂度分析

跳表的时间复杂度：

  1. 查找操作：
  • 在跳表中进行查找操作时，从最高层开始，每一层最多进行一次比较和移动，直到找到目标元素或者到达底层。
  • 由于每一层的节点数量逐渐增多，但节点之间的跨度也逐渐增大，因此在平均情况下，查找操作的时间复杂度为 O ( l o g n ) O(log n) O(logn)，其中 n n n 是跳表中的元素数量。
  1. 插入操作：
  • 插入操作首先需要进行查找，以确定插入的位置。这个查找过程的时间复杂度为 O ( l o g N ) O(logN) O(logN)。
  • 然后，根据随机生成的层数，进行节点的插入操作。插入操作本身的时间复杂度是常数级别的，因为只需要调整一些指针。
  • 总体来说，插入操作的时间复杂度也为 O ( l o g N ) O(logN) O(logN)。
  1. 删除操作：
  • 删除操作同样先进行查找，找到要删除的元素。查找过程的时间复杂度为 O ( l o g N ) O(logN) O(logN)。
  • 一旦找到要删除的元素，只需要调整一些指针来删除该元素，时间复杂度也是常数级别的。
  • 所以删除操作的时间复杂度也是 O ( l o g N ) O(logN) O(logN)。

跳表的空间复杂度：

  1. 空间占用：
  • 跳表的空间复杂度主要取决于节点的数量和层数。
  • 在最理想的情况下，跳表的层数为 l o g N log N logN，其中 N N N 是元素数量。每个节点除了存储自身的值外，还需要存储指向不同层下一个节点的指针。
  • 如果每层的指针占用固定的空间，那么总体的空间复杂度为 O ( N ) O(N) O(N)，其中 N N N 是元素数量。
  1. 额外空间：
  • 考虑到跳表在插入元素时需要随机生成层数，可能会有一些额外的空间开销用于存储随机数生成的状态等。但这些额外的空间开销相对较小，不会对总体的空间复杂度产生主要影响。

综上所述，跳表的时间复杂度为 O ( l o g N ) O(log N) O(logN)，空间复杂度为 O ( N ) O(N) O(N)。

6. 跳表与平衡搜索树/哈希表的对比

以下是跳表与平衡搜索树（以 AVL 树和红黑树为例）以及哈希表的对比总结：
一、跳表与平衡搜索树对比

  1. 实现复杂度：
  • 跳表实现相对简单，容易控制。在增删查改和遍历操作上，平衡树更加复杂。
  1. 空间消耗：
  • 当跳表中参数 p = 1 / 2 p = 1/2 p=1/2 时，每个节点平均指针数目为 2；当 p = 1 / 4 p = 1/4 p=1/4 时，平均指针数目为 1.33。而平衡树的节点需要存储三叉链、平衡因子或颜色等信息，空间消耗相对较大。

二、跳表与哈希表对比

  1. 时间复杂度：
    • 哈希表平均时间复杂度为 O ( 1 ) O(1) O(1)，比跳表快。
  2. 空间消耗：
    • 哈希表空间消耗略多一点。跳表相对空间消耗略小，因为哈希表存在链接指针和表空间消耗。
  3. 其他方面：
    • 跳表的优势在于遍历数据有序，而哈希表无序。
    • 哈希表扩容时有性能损耗。
    • 在极端场景下，哈希冲突高时效率下降厉害，需要红黑树等补足接力，而跳表不存在此问题。

总体而言，跳表在实现复杂度和空间消耗上有一定优势，与平衡搜索树一样能保证数据有序遍历，虽然时间复杂度不如哈希表，但在一些需要有序性且对实现复杂度和空间有要求的场景下，跳表是一个不错的选择。

7. 源码

template<class T>
struct SkipListNode
{
	T _val;
	vector<SkipListNode*> _nextV;
	SkipListNode(const T& val,int level)
		:_val(val)
		,_nextV(level,nullptr)
	{}
};
template<class T>
class SkipList
{
	typedef SkipListNode<T> Node;
public:
	SkipList()
	{
		srand((unsigned int)time(NULL));
		_head = new Node(T(), 1);//初始化一个头节点
	}
	bool Search(int target)
	{
		Node* cur = _head;
		//从最高层开始筛选
		int level = _head->_nextV.size() - 1;
		while (level >= 0)
		{
			//大于往右走
			if (cur->_nextV[level] && target > cur->_nextV[level]->_val)
			{
				cur = cur->_nextV[level];
			}
			//为空或者小于等于往下走
			else if (cur->_nextV[level] == nullptr || target < cur->_nextV[level]->_val)
			{
				--level;
			}
			//相当返回true
			else
			{
				return true;
			}
		}
		return false;
	}
	void Add(int num)
	{
		//寻找前驱节点
		vector<Node*> preV = FindPrevNode(num);
		//随机层数
		int level = RandomLevel();
		Node* newnode = new Node(num, level);
		//如果超过最大层数
		if (level > _head->_nextV.size())
		{
			_head->_nextV.resize(level, nullptr);
			preV.resize(level, _head);
		}
		//链接前后节点
		for (int i = 0; i < level; i++)
		{
			newnode->_nextV[i] = preV[i]->_nextV[i];
			preV[i]->_nextV[i] = newnode;
		}
	}
	bool Erase(int num)
	{
		vector<Node*> preV = FindPrevNode(num);
		// 第一层下一个不是val，则val不在跳表中
		if (preV[0]->_nextV[0] == nullptr || preV[0]->_nextV[0]->_val != num)
		{
			return false;
		}
		//删除节点
		Node* del = preV[0]->_nextV[0];

		// del结点每一层前后指针链接起来
		for (size_t i = 0; i < del->_nextV.size(); i++)
		{
			preV[i]->_nextV[i] = del->_nextV[i];
		}
		delete del;

		// 如果删除最高层结点，把头节点的层数也降一下
		int i = _head->_nextV.size() - 1;
		while (i >= 0)
		{
			//直接为空
			if (!_head->_nextV[i])
			{
				i--;
			}
			else
			{
				break;
			}
		}
		//调整
		_head->_nextV.resize(i + 1);
		return true;
	}
	//寻找前驱节点集合
	vector<Node*> FindPrevNode(int num)
	{
		Node* cur = _head;
		//从最高层开始筛选
		int level = _head->_nextV.size() - 1;
		vector<Node*> preV(level + 1, nullptr);
		while (level >= 0)
		{
			//大于往右走
			if (cur->_nextV[level] && num > cur->_nextV[level]->_val)
			{
				cur = cur->_nextV[level];
			}
			//为空或者小于等于往下走
			else if (cur->_nextV[level] == nullptr || num <= cur->_nextV[level]->_val)
			{
				preV[level--] = cur;
			}
		}
		return preV;
	}
	//生成随机层数
	int RandomLevel()
	{
		size_t level = 1;

		// rand() / RAND_MAX -> [0, 1]
		while (rand() <= RAND_MAX * _p && level <= _maxLevel)
		{
			level++;
		}
		return level;
	}
	// 析构函数
	~SkipList()
	{
		Node* cur = _head;
		while (cur)
		{
			//保存下一个节点
			Node* next = cur->_nextV[0];
			delete cur;
			cur = next;
		}
	}
private:
	Node* _head;
	size_t _maxLevel = 32;
	double _p = 0.25;
};

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/2072261.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【数据存储】大/小端存储与字节顺序转换函数详解

【数据存储】大/小端存储与字节顺序转换函数详解

学习目的是使用&#xff0c;网络编程中主机字节顺序与网络字节顺序转换这块就用到了这些概念及其函数&#xff01; 【Linux网络编程入门】Day5_socket编程基础 文章目录&#xff1a; 大端存储与小端存储 1.1 低地址与高地址 1.2 数据的高位与低位 1.3 大端存储 1.3.1 定义 1.…
阅读更多...
轻松打造一个可以切换AI平台的网站

轻松打造一个可以切换AI平台的网站

亮色主题 暗色主题 停止按键 设置界面 浏览器缓存设置 Kimi 通义千问 ChatGPT 手机版 部分代码如下&#xff1a; # -*- coding: utf-8 -*- from flask import Flask, request, jsonify, render_template, Response import requests import json import os from gevent import p…
阅读更多...
Go反射四讲---第二讲：反射与结构体，使用反射如何操纵结构体？

Go反射四讲---第二讲：反射与结构体，使用反射如何操纵结构体？

反射-结构体 这是我们反射四讲的第二讲&#xff0c;本次给大家讲解如何使用反射处理结构体。 使用反射如何输出结构体的字段名字和值,使用反射如何给结构体字段设置值。 为了确保反射输出所有的字段名字和值&#xff0c;关键在于一点只有 Kind Struct 的才有。 注意&#…
阅读更多...
Neo4J下载安装

Neo4J下载安装

Windows 版本 1、 下载链接安装JDK 下载链接 https://download.oracle.com/java/22/latest/jdk-22_windows-x64_bin.msi 下载完毕后默认安装即可 2、 下载Neo4J 进入Neo4j Deployment Center - Graph Database & Analytics下载页面&#xff0c;选择社区版&#xff0c;…
阅读更多...
CentOS全面停服，国产化提速，央国企信创即时通讯/协同门户如何选型？

CentOS全面停服，国产化提速，央国企信创即时通讯/协同门户如何选型？

01. CentOS停服带来安全新风险&#xff0c; 国产操作系统迎来新的发展机遇 2024年6月30日&#xff0c;CentOS 7版本全面停服&#xff0c;于2014年发布的开源类服务器操作系统——CentOS全系列版本生命周期画上了句号。国内大量基于CentOS开发和适配的服务器及平台&#xff0c…
阅读更多...
笔记小结：《利用python进行数据分析》之使用pandas和seaborn绘图

笔记小结：《利用python进行数据分析》之使用pandas和seaborn绘图

matplotlib实际上是一种比较低级的工具。要绘制一张图表&#xff0c;你组装一些基本组件就行&#xff1a;数据展示&#xff08;即图表类型&#xff1a;线型图、柱状图、盒形图、散布图、等值线图等&#xff09;、图例、标题、刻度标签以及其他注解型信息。 在pandas中&#xf…
阅读更多...
pyyaml：Python 中的 YAML 处理大师

pyyaml：Python 中的 YAML 处理大师

文章目录 pyyaml&#xff1a;Python 中的 YAML 处理大师背景&#xff1a;为何选择 pyyaml&#xff1f;pyyaml 是什么&#xff1f;如何安装 pyyaml&#xff1f;五个简单的 pyyaml 库函数使用方法1. 加载 YAML 数据2. 转储 YAML 数据3. 从文件加载 YAML4. 将数据写入 YAML 文件5.…
阅读更多...
Cockos Reaper：开启专业数字音频制作之旅

Cockos Reaper：开启专业数字音频制作之旅

Cockos Reaper 是一款备受赞誉的专业数字音频制作软件&#xff0c;适用于 Mac 和 Windows 系统。它以其强大的功能和高度的灵活性&#xff0c;成为众多音乐人和音频制作人的首选工具。 在音乐创作方面&#xff0c;Reaper 提供了丰富的虚拟乐器和音频效果插件&#xff0c;让你能…
阅读更多...
如何使用ssm实现ssm框架的购物网站+vue

如何使用ssm实现ssm框架的购物网站+vue

TOC ssm113ssm框架的购物网站vue 绪论 1.1 研究背景 当前社会各行业领域竞争压力非常大&#xff0c;随着当前时代的信息化&#xff0c;科学化发展&#xff0c;让社会各行业领域都争相使用新的信息技术&#xff0c;对行业内的各种相关数据进行科学化&#xff0c;规范化管理。…
阅读更多...
AI 绘画神器 Midjourney 基础使用手册

AI 绘画神器 Midjourney 基础使用手册

一、前提条件 需要魔法&#xff1a; 新用户可免费创作 25 张图片&#xff0c;超过需要办会员版权问题&#xff1a;会员生成的图片版权归创作者所有 二、注册/链接 服务器 温馨提示&#xff1a;下方多图预警 1. 注册、创建服务器 ① 打开Midjourney官网&#xff0c;右下角…
阅读更多...
机器学习入门指南：如何构建智能预测模型

机器学习入门指南：如何构建智能预测模型

【机器学习】&#xff1a;入门从零开始的指南 随着人工智能的快速发展&#xff0c;机器学习&#xff08;Machine Learning&#xff09;已经成为技术领域的热点话题。无论是推荐系统、语音识别、自动驾驶汽车&#xff0c;还是自然语言处理&#xff0c;机器学习的应用随处可见。…
阅读更多...
minio文件存储

minio文件存储

文章目录 参考安装与部署springboot整合miniopom.xmlapplication.ymlMinioPropertiesMinioConfigMinioApp测试基本功能bucket是否存在创建bucket修改bucket的访问权限查询所有的bucket删除指定的bucket上传文件到minio查看对象的描述信息获取文件的预签名访问地址后台获取minio…
阅读更多...
第二课《动态规划》

第二课《动态规划》

1.1.1 线性dp 2.1.1 区间dp 3.1.1 背包dp 动态规划理论 动态规划算法通常用于求解具有某种最优性质的问题。在这类问题中&#xff0c; 可能会有很多可行解。没一个解都对应于一个值&#xff0c;我们希望找到具有最优值的解。胎动规划算法与分治法类似&#xff0c;其基本思想…
阅读更多...
数据丢失不再怕！2024年高效硬盘恢复软件精选

数据丢失不再怕！2024年高效硬盘恢复软件精选

硬盘数据丢失或文件损坏等问题&#xff0c;这不仅会影响我们的日常工作与生活&#xff0c;还可能造成无法挽回的损失。随着技术的发展&#xff0c;市场上涌现出了众多硬盘数据恢复软件。本文将为您介绍几款主流且高效的硬盘文件修复工具&#xff0c;希望能为您在数据遭遇不测时…
阅读更多...
《深入浅出WPF》读书笔记.6binding系统(下)

《深入浅出WPF》读书笔记.6binding系统(下)

《深入浅出WPF》读书笔记.6binding系统(下) 背景 主要讲数据校验和数据转换以及multibinding 代码 binding的数据校验 <Window x:Class"BindingSysDemo.ValidationRulesDemo"xmlns"http://schemas.microsoft.com/winfx/2006/xaml/presentation"xmln…
阅读更多...
innodb_buffer_pool_size在线缩小操作

innodb_buffer_pool_size在线缩小操作

一、背景 测试数据库内存32G&#xff0c;只有MySQL数据库&#xff0c;但是innodb_buffer_pool_size设置了24G&#xff0c;导致经常出现lack of memory问题、lack of swap问题。 因为使用了MySQL5.7.36版本&#xff0c;利用innodb_buffer_pool_size参数值可在线调整的新特性&…
阅读更多...
这个TOP 100 AI应用榜单，包含了所有你需要的使用场景（一）

这个TOP 100 AI应用榜单，包含了所有你需要的使用场景（一）

大家好&#xff0c;我是木易&#xff0c;一个持续关注AI领域的互联网技术产品经理&#xff0c;国内Top2本科&#xff0c;美国Top10 CS研究生&#xff0c;MBA。我坚信AI是普通人变强的“外挂”&#xff0c;专注于分享AI全维度知识&#xff0c;包括但不限于AI科普&#xff0c;AI工…
阅读更多...
【源码+文档+调试讲解】劳务外包管理系统的设计与实现

【源码+文档+调试讲解】劳务外包管理系统的设计与实现

摘 要 互联网发展至今&#xff0c;无论是其理论还是技术都已经成熟&#xff0c;而且它广泛参与在社会中的方方面面。它让信息都可以通过网络传播&#xff0c;搭配信息管理工具可以很好地为人们提供服务。针对劳务外包信息管理混乱&#xff0c;出错率高&#xff0c;信息安全性差…
阅读更多...
微分方程（Blanchard Differential Equations 4th）中文版Section3.7

微分方程（Blanchard Differential Equations 4th）中文版Section3.7

迹-行列式平面上平面系统分析 在前面的章节中，我们遇到了许多不同类型的线性微分方程系统。到目前为止，可能会觉得这些系统有很多不同的可能性，每种都有其独特的特征。为了将这些例子放在整体视角下进行回顾，创建一个表格是一个有用的方法。 总结我们到目前为止所做的工作…
阅读更多...
基于SHAP进行特征选择和贡献度计算——可解释性机器学习

基于SHAP进行特征选择和贡献度计算——可解释性机器学习

方法介绍 SHAP&#xff08;SHapley Additive exPlanations&#xff09;是一个 Python 包&#xff0c;旨在解释任何机器学习模型的输出。SHAP 的名称源自合作博弈论中的 Shapley 值&#xff0c;它构建了一个加性的解释模型&#xff0c;将所有特征视为“贡献者”。对于每个预测样…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023