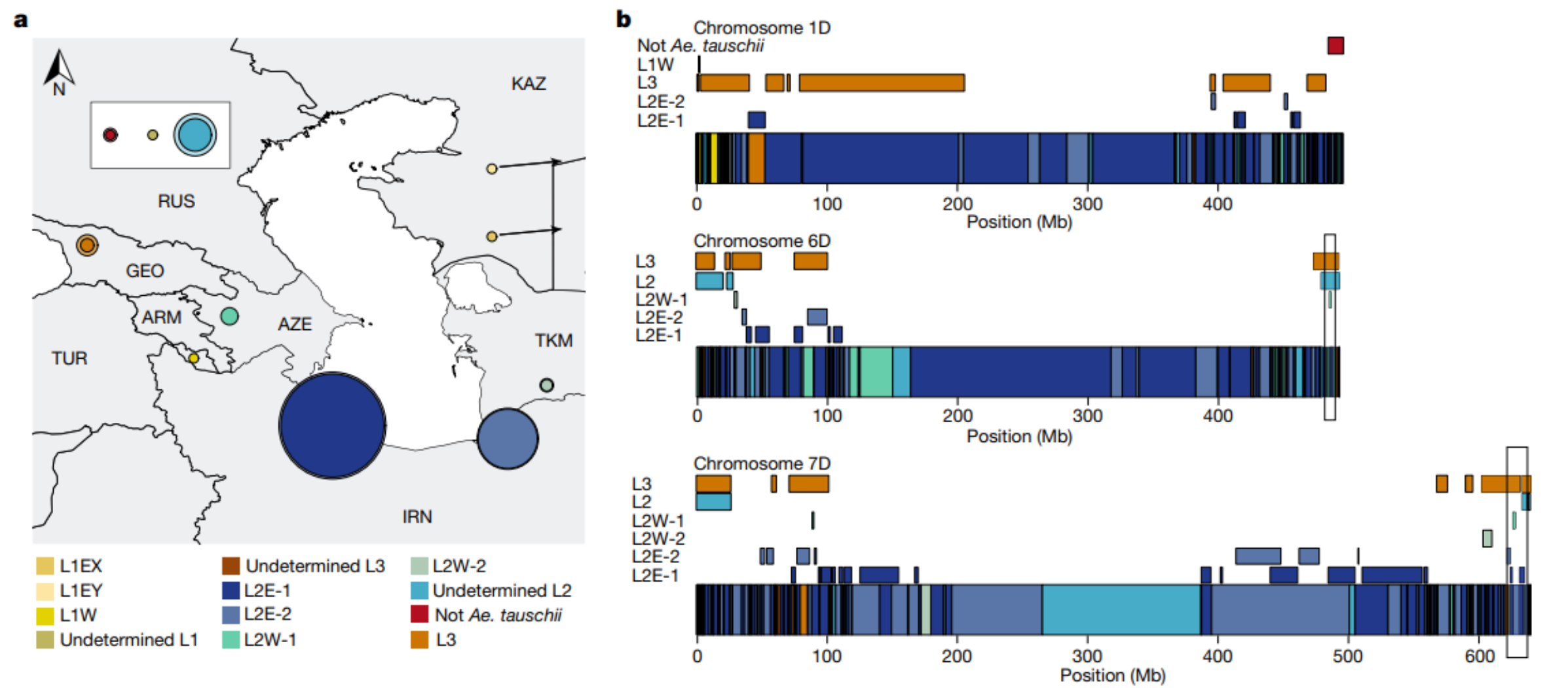
集合可以用二进制表示，二进制从低到高第 i 位为 1 表示 i 在集合中，为 0 表示 i 不在集合中。例如集合 {0,2,3} 可以用二进制数 1101(2)​ 表示；反过来，二进制数 1101(2)​ 就对应着集合 {0,2,3}。

例如集合 {0,2,3} 可以压缩成 20+22+23=13，也就是二进制数 1101(2)​。

一、集合与集合

其中 & 表示按位与，| 表示按位或，⊕ 表示按位异或，~ 表示按位取反。

两个集合的「对称差」是只属于其中一个集合，而不属于另一个集合的元素组成的集合，也就是不在交集中的元素组成的集合。

注 1：按位取反的例子中，仅列出最低 4个比特位取反后的结果，即 0110 取反后是 1001。

注 2：包含于的两种位运算写法是等价的，在编程时只需判断其中任意一种。

注 3：编程时，请注意运算符的优先级。例如 == 在某些语言中优先级比位运算更高。

二、集合与元素

在处理集合与元素的关系时，通常会用到移位运算。

其中 << 表示左移，>> 表示右移。

注：左移 i 位相当于乘以 2i，右移 i 位相当于除以 2i（注意，这里的除法指的是整数除法，即结果向下取整）。

      s = 101100
    s-1 = 101011 // 最低位的 1 变成 0，同时 1 右边的 0 都取反，变成 1
s&(s-1) = 101000

特别地，如果 s 是 2 的幂，那么 s&(s−1)=0。

此外，编程语言提供了一些和二进制有关的库函数，例如：

• 计算二进制中 1 的个数，也就是集合大小；
• 计算二进制长度（位数），减一后得到集合中最大元素的索引（注意，这里通常指的是从0开始计数的索引，如果要得到实际的元素值，则需要根据位数计算，即 2位数−1）；
• 计算二进制尾零个数，这个操作通常用于获取最低位的 1 之前的 0 的个数，但直接将其解释为集合最小元素可能不太准确，因为集合中的元素通常是从 0 或 1 开始的连续整数。不过，在某些特定场景下，这个信息可能有助于推断集合的某些性质。

调用这些函数的时间复杂度通常是 O(1)，意味着它们可以在常数时间内完成计算，不随输入规模的增长而增长。

特别地，只包含最小元素的子集，即二进制最低 11及其后面的 0，也叫 lowbit，可以用 s & -s 算出。举例说明：

     s = 101100
    ~s = 010011
(~s)+1 = 010100 // 根据补码的定义，这就是 -s  =>  s 的最低 1 左侧取反，右侧不变
s & -s = 000100 // lowbit

三、遍历集合

设元素范围从 0 到 n−1，枚举范围中的元素 i，判断 i 是否在集合 s 中。

for (int i = 0; i < n; i++) {
    if (((s >> i) & 1) == 1) { // i 在 s 中
        // 处理 i 的逻辑
    }
}

也可以直接遍历集合 s 中的元素：不断地计算集合最小元素、去掉最小元素，直到集合为空。

for (int t = s; t > 0; t &= t - 1) {
    int i = Integer.numberOfTrailingZeros(t);
    // 处理 i 的逻辑
}

四、枚举集合

枚举所有集合

设元素范围从 0 到 n−1，从空集 ∅ 枚举到全集 U：

for (int s = 0; s < (1 << n); s++) {
    // 处理 s 的逻辑
}

枚举非空子集

设集合为 s，从大到小枚举 s 的所有非空子集 sub：

for (int sub = s; sub > 0; sub = (sub - 1) & s) {
    // 处理 sub 的逻辑
}

枚举子集（包含空集）

如果要从大到小枚举 ss的所有子集 sub（从 ss枚举到空集 ∅），可以这样写：

int sub = s;
do {
    // 处理 sub 的逻辑
    sub = (sub - 1) & s;
} while (sub != s);

原理是：当 sub=0（空集）时，再减一就得到 -1，对应的二进制为 111⋯1。然后再与 s 进行按位与操作（&），就得到了 s。所以当循环到 sub=s 时，说明最后一次循环的 sub=0（空集），s 的所有子集都枚举到了，此时可以退出循环。

Gosper's Hack（枚举全集 U 的所有大小恰好为 k 的子集）

public class GospersHack {  
      
    // 打印一个整数表示的子集，其中集合是 0 到 n-1 的整数  
    private static void printSubset(int subset, int n) {  
        for (int i = 0; i < n; i++) {  
            if ((subset & (1 << i)) != 0) {  
                System.out.print(i + " ");  
            }  
        }  
        System.out.println();  
    }  
      
    // 使用 Gosper's Hack 枚举所有大小为 k 的子集  
    public static void enumerateSubsets(int n, int k) {  
        // 初始子集是所有最低位的 k 个 1  
        int subset = (1 << k) - 1;  
          
        // 循环直到达到上限（所有 n 个位中的 k 个 1 的最大子集）  
        while (true) {  
            // 打印当前子集  
            printSubset(subset, n);  
              
            // 查找需要翻转的最低位的 1（即需要向右移动的最低位的 1）  
            int x = subset & -subset; // 找到最低位的 1  
            int y = subset + x; // 将该位及其左边的所有位设为 1  
              
            // 清除 y 中从最低位的 1 到最右边的 1 之间的所有位  
            y = (y / x) >> 1;  
              
            // 翻转 y 中最右边的 1 及其右边的所有位  
            subset = subset ^ y;  
              
            // 检查是否已经生成了所有子集  
            if ((subset & (1 << (k - 1))) == 0) {  
                break;  
            }  
        }  
    }  
      
    public static void main(String[] args) {  
        int n = 4; // 集合大小  
        int k = 2; // 子集大小  
        enumerateSubsets(n, k);  
    }  
}