1. LeetCode84(柱状图中最大的矩形)
给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。
求在该柱状图中,能够勾勒出来的矩形的最大面积。
示例 1:
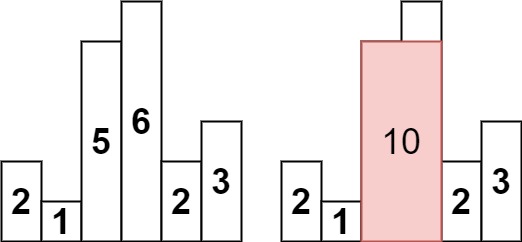
输入:heights = [2,1,5,6,2,3]
输出:10
解释:最大的矩形为图中红色区域,面积为 10示例 2:
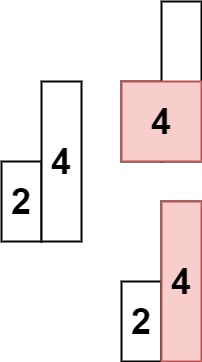
输入: heights = [2,4]
输出: 4提示:
1 <= heights.length <=10^50 <= heights[i] <= 10^4
如题意描述,要取最大的矩形面积,那么得找到宽度与高度相乘的最大值.
但我们先思考几个情形,在这张图上什么样能构成矩形
- 长和宽都得规则,也就是只能是水平扩展,不能是不规则的扩展.
- 对于每一个柱形,他自己本身也是一个矩形.
基于以上的描述,接下来我们就得找到构成矩形的长宽,从何处取.
对于每一个柱形,我们得先选取一个基准.什么叫基准呢,就是以这个柱子的高度,去找寻能够凑成与这个柱子构成的矩形.
可能还是很模糊,我们举具体的例子来说明:
- 例如我们来查看索引1处这个柱子
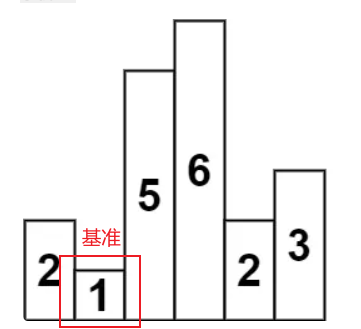
以他为基准,我们想要尽可能的扩展这个矩形,那么说明什么?我们需要找到左边第一个比他小的柱子高度与右边比他小的第一个柱子的高度.
为什么呢,为什么水平扩展就得去要找到比他小的值呢?
因为第一个比他小的说明,只能扩展在这个索引处,不能再往左或者右方向扩展.
如果没找到呢,说明能够完全扩展到左右两端,例如此时的1.左右两端都没有出现比他小的高度,所以以他为基准.所构成的矩形面积大小为 1 * 6 = 6.
所以关键点出来了,我们得找到在左边第一个比此时柱子小的高度,与第一个右边比此时柱子小的高度.
所以我们此时才会想到单调栈,单调栈的使用场景就有我们需要找到第一个比他小或者大的数.
那问题来了,栈里面是调递增呢,还是递减呢
注意:
- 要找第一个比他小的,栈里面递减
- 要找第一个比他大的,栈里面递增
所以我们的栈里面是单调递减的.这样我们再来解释一下,如何从这样一个单调栈中找到第一个比此时柱子高度小的值.
- 对于柱子右边来讲,我们很好理解,遇见比此时栈顶元素(这个栈顶元素也就是我们之前提到的基准)小的数时,说明此时遇到基准第一个小的值(从左往右遍历的,遇见一个比他小的肯定就是第一个比他小的)
- 而对于右边的第一个最小值呢?实际上就是基准从栈弹出后的下一个栈顶元素,别忘了栈里面是单调递减的,所以弹出当前栈顶元素,下一个栈顶一定是小于等于上一个的栈顶元素.
这样我们就能找到左边第一个与右边第一个比他小的值,那怎么计算这样的宽度呢?
我们观察一下 5 6 2这一段柱子
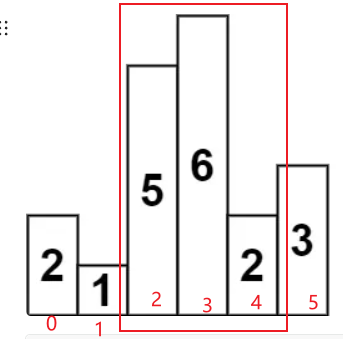
对于我们这样的算法思想,当遍历到2时,此时他是小于栈顶元素6的.所以我们要触发计算过程.
宽度如何确认呢?注意我们单调栈中存的应该是数组中的下标,我们再通过下标找到数组具体的值,相当于做了一个映射.
所以依照我们的思想
基准: mid = stack.pop() //此时应该是3(下标,对应就是数组中的6)
第一个左边比他小的值: left = stack.peek() //是2(下标,对应就是数组中的5)
第一个右边比他小的值: right = i //就是此时遍历到数组的下标(对应数组中的2)
这样一看,对于此时基准6而言,左右都不能扩展,此时算出的矩形面积应该就是他自己本身构成的矩形
面积为: height[mid] * (right - left - 1)
这样我们就得到了面积的计算公式.
此时我们考虑情况完了吗?
并没有,假设此时有这样一个数组: [1,3,6,7,9]
我们会发现数组本身就是单调的,这样按照我们之前的思路,会导致全部存入栈中,而没有产生计算.那我们如何去触发计算呢?
实际上我们在尾部填上一个0就可以啦,因为0肯定是小于数组中的元素(题目说了值大于等于0),这样就会触发我们的计算过程.
那这样就万无一失了吗?还不够,我们再试想一个数组:[9,7,6,3,1]
对于这样一个数组,在遇见7时,我们会把9弹出,但再去找栈顶元素时,栈中已经没有了值,所以我们获取不到,导致算法过程不能正常执行.所以此时我们还需要来往数组前添加一个0,来确保我们的计算逻辑的一致性.
所以整体代码为:
class Solution {
public int largestRectangleArea(int[] heights) {
LinkedList<Integer> stack = new LinkedList();
int max = 0;
//后补0为了能够触发计算的操作,前补0为了整个计算逻辑
int[] height = new int[heights.length + 2];
for(int i = 1,j = 0;i < height.length - 1;j++,i++){
height[i] = heights[j];
}
for(int i = 0;i < height.length;i++){
while(!stack.isEmpty() && height[stack.peek()] > height[i]){
//mid代表基准
int mid = stack.pop();
//left代表左边第一个比基准小的索引值,也就是以当前基准能够扩展到左边的哪个位置
int left = stack.peek();
//right代表右边第一个比基准小的索引值,也就是以当前基准能够扩展到右边的哪个位置
int right = i;
max = Math.max(max,height[mid] * (right - left - 1));
}
stack.push(i);
}
return max;
}
}