判别分析2|Bayes判别分析|Fisher判别分析|软件求解

Bayes判别分析

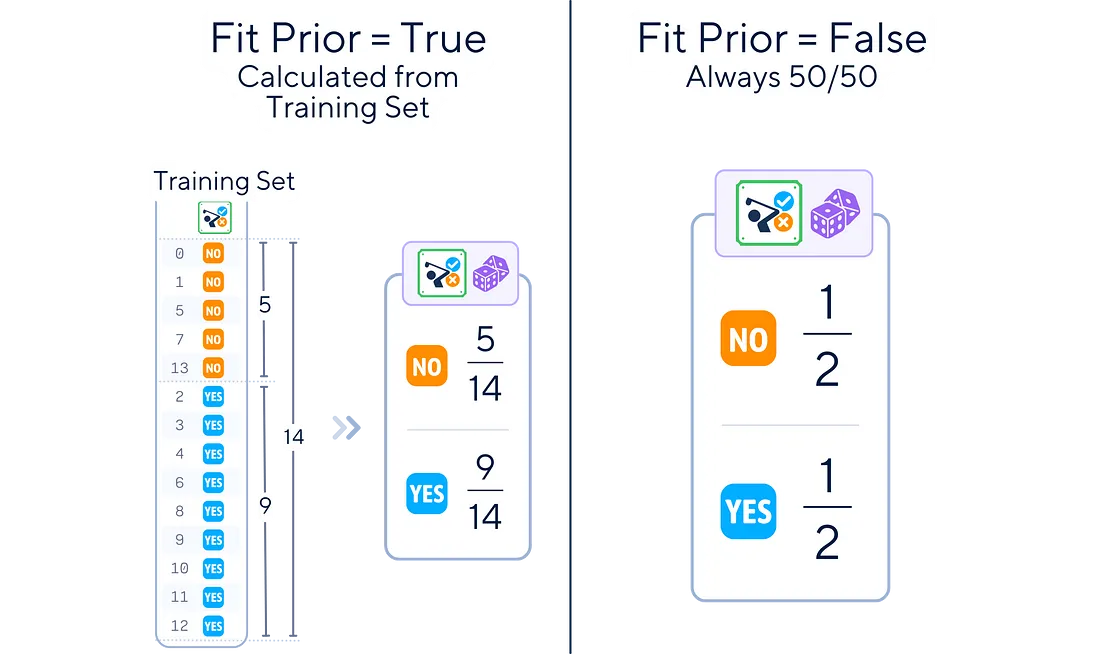
引入先验信息

距离判别只要求知道总体的数字特征，不涉及总体的分布函数
当均值和协方差未知时，就用样本的均值和协方差矩阵做估计值。距离判别方法简单实用，但没有考虑到每个总体出现的机会大小，即先验概率，没有考虑到错判的损失。比如医疗诊断中癌症病人和正常人的分辨。贝叶斯判别法正是为了解决这两个问题提出的判别分析方法

Bayes统计的基本思想是：假定对所研究的对象已有一定的认识，常用先验概率分布来描述这种认识，然后我们取得一个样本，用样本来修正已有的认识（先验概率分布），得到后验概率分布，各种统计推断都通过后验概率分布来进行。将Bayes思想用于判别分析，就得到贝叶斯分类器。贝叶斯公式如下：
$P(B_{i}| A)=\frac{P(A| B_{i})P(B_{i})}{\sum P(A| B_{i})P(B_{i})}$

贝叶斯分类器：
判别函数：后验概率计算公式，
判别准则：后验概率最大原则
设有总体 $G_{i}(i=1,2,\dots,k)$ ，具有概率密度函数 $f_{i}(x)$ ，并且有先验知识
知道 $G_{i}$ 发生的概率是 $P_{i}$ 。由贝叶斯公式计算样本 $x_{0}\in G_{i}$
后验概率为：
$P(G_{i}| x_{0})= \frac{p_{i}f_{i}(x_{0})}{\sum p_{j}f_{j}(x_{0})}$
判别规则：若
$P(G_{l}| x_{0})= \frac{p_{l}f_{l}(x_{0})}{\sum p_{j}f_{j}(x_{0})}=max_{1\le i\le k} \frac{p_{i}f_{i}(x_{0})}{\sum p_{j}f_{j}(x_{0})}$
则 $x_{0}$ 判给 $G_{l}$
若要同时考虑到错判的损失，模型可进一步修正。设C(j/i)表示将第i类错判到第j类所造成的损失。请看下面Bayes判别准则。

定理：若各类总体 $G_{1},G_{2},\dots,G_{k}$ 的先验概率为
$\left\{ a_{i},i=1,2,3,\dots,k\right\}$
各类密度函数 $\left\{ f_{i}(x)\right\}$ 。第i类错判到第j类所造成的损失 $\left\{ C(j/i)\right\}$
构造判别函数
$h_{j}(x)=\sum_{j=1}^{k} q_{i}C(j/i)f_{i}(x)$
对任意样本x，判别规则是
若
$h_{i}(x)=min_{1\le j\le k}h_{j}(x)$
则 $\in G_{i},\ i= 1,2,3,\dots,k$
$\left\{ h_{j}(x)\right\}$ 描述了将其他类样本划分到第j类的可能产生的损失。
这个判别规则，理论上使平均错判损失最小。

两类问题时的Bayes判别准则为
$x\in G_{1},\ 若q_{2}C(1/2)f_{2}(x)-q_{1}C(2/1)f_{1}(x)<0$
$\frac{f_{1}(x)}{f_{2}(x)}> \frac{q_{2}C(2/1)}{q_{1}C(1/2)}$
令
$v(x)=\frac{f_{1}(x)}{f_{2}(x)},\ d=\frac{q_{2}C(2/1)}{q_{1}C(1/2)}$
$\left\{\begin{matrix} x\in G_{1}\quad 若v(x)>d \\ x\in G_{2}\quad 若v(x)<d \\ 待判\quad 若v(x)=d \end{matrix}\right.$
当给定不同的分布假设时，判别函数 $v (x)$ 具有更简单形式
当两总体错分损失相等时，两个总体的Bayes判别法则为：
$\left\{\begin{matrix} x\in G_{1}:若P(G_{1}| x)\ge P(G_{2}|x) \\ x\in G_{2}:若P(G_{1}| x)< P(G_{2}|x) \end{matrix}\right.$
更进一步对正态分布分类总体：
若两总体的协方差矩阵相等，化解上述的判别规则得到等价的线性判别规则
若协方差矩阵不相等，则判别函数为二次函数。
再进一步，当p1=p2时，Bayes判别就是距离判别
Bayes分类器有很高的理论价值，在实际使用时有很多的假设难以满足

Fisher判别分析

首先考虑只有两个属性变量的二分类判别分析问题。
分类思想就寻找一个方向，也就是图上的虚线方向，沿着这个方向朝和这个虚线垂直的一条直线进行投影会使得这两类分得最清楚。可以看出，如果向其他方向投影，判别效果不会比这个好。
![[Pasted image 20240823153937.png]]

投影之后，再用前面讲到的距离判别方法对样本进行分类
费歇（Fisher）判别法是一种线性判别的方法。它的工作思路是对原数据系统进行坐标变换，寻求能将类别总体尽可能分开的投影方向，使得投影后的数据点，同一类别的尽量聚拢，不同类别产生的尽量拉开。
优点：没有做分布假设。

Fisher判别函数或典型判别函数
$\hat{Y}_{1}(x)=\hat{c}_{11}x_{1}+\dots+\hat{c}_{p1}x_{p}$
寻找一个投影方向
$(\hat{c}_{11},\hat{c}_{21},\dots,\hat{c}_{p1},)^{T}$
样本点投影后的点集
$\left\{ \hat{c}_{11}x_{1i}+\dots+\hat{c}_{p1}x_{pi} \right\}_{i=1}^{n}$
计算该点集的组内离差平方和、组间离差平方和
$\frac{组间离差平方和}{组内方差和}$
选择方向 $(\hat{c}_{11},\hat{c}_{21},\dots,\hat{c}_{p1},)^{T}$ 应使得I值达到最大。

在这个方向，最大限度地反映不同类的个体之间的差异，在这个方向上产生的变量称之为第一个典型变量
$\hat{Y}_{1}(x)=\hat{c}_{11}x_{1}+\dots+\hat{c}_{p1}x_{p}$
就是第一个典型判别函数。同样通过投影可以找到第二个方向，建立第二个典型变量，和第二个典型判别函数。直到找到t个。 $t\le k$ 。
k是总体的个数。

使用典型判别函数判别×的类

把所有类的各个指标的均值（非标准化数据的均值），代入典型判别函数，得出各类中心典型函数的值
把需要判别的点x的p个指标的值，代入典型判别函数，得出这个点的典型函数值，与哪个类中心的典型函数值最近，就判别这个点属于这个类（投影后最近距离判别）

两类问题时，设有
$\left\{ X_{1}^{(1)},X_{2}^{(1)},\dots,X_{n1}^{(1)} \right\}\in G_{1},\ \left\{ X_{1}^{(2)},X_{2}^{(2)},\dots,X_{n_{2}}^{(2)} \right\}\in G_{2},\$
一个投影方向和典型判别函数
$U=(c_{1},c_{2},\dots,c_{p})^{T},\ Y_{1}(x)=c_{11}x_{1}+\dots+c_{p1}x_{p}$
投影后类中心
$\left\{ u^{T}X_{1}^{(1)},u^{T}X_{2}^{(1)},\dots,u^{T}X_{n1}^{(1)} \right\}\quad 类中心G_{1}$
$\left\{ u^{T}X_{1}^{(2)},u^{T}X_{2}^{(2)},\dots,u^{T}X_{n_{2}}^{(2)} \right\}\quad 类中心G_{2}$
待判样品x到某一类G的距离定义为X点与类中心的距离
$d(X,G_{1})=| | u^{T}X -C_{1}| |,\ d(X,G_{2})=| | u^{T}X-C_{2} | |$
Fisher分类判别准则为
$\left\{\begin{matrix} d(X,G_{1})<d(X,H_{2}),\ 则X\in G_{1} \\ d(X,G_{2})<d(X,H_{1}),\ 则X\in G_{2} \\ d(X,G_{1})=d(X,H_{2}),\ 则X待定 \end{matrix}\right.$

典型函数判别能力检验

当需要多个典型函数时，对典型函数的判别能力要通过显著性检验来取舍。
多元方差分析可以检验所有属性变量是否联合对判别函数的判别能力有显著性意义
在一个判别函数中，每一个属性变量对典型函数的判别能力都有所贡献。贡献的大小可以用多元方差分析来检验。
属性变量的判别能力重要性也各不相同。类似逐步回归，也可选择遂步判别分析法

逐步判别法的基本思想是采用“有进有出”的算法，即遂步引入变量、每引入一个“最重要”的变量进入判别式，同时也考虑较早引入判别式的某些变量，如果其判别能力随新弓入变量而变为不显著了（例如其作用被后引入的某几个变量的组合所代替），应及时从判别式中把它剔除去，直到判别式中没有不重要的变量需要剔除，而剩下来的变量也没有重要的变量可引入判别式时，逐步筛选结束。这个筛选过程实质就是作假设检验，通过检验找出显著性变量，剔除不显著变量。

软件求解

SPSS判别分析求解

IrisDataSet（鸢尾属植物数据集）是被用来介绍线性判别式分析最悠久的数据集。在这个数据集中，包括了三类不同的鸢尾属植物：IrisSetosa，Iris
Versicolour，IrisVirginica。每类收集了50个样本，因此这个数据集一共包含了 150个样本。
该数据集测量了所有150个样本的4个特征，分别是：
sepal length (花萼长度)
sepal width (花萼宽度)
petal length (花瓣长度)
petal width (花瓣宽度)
以上四个特征的单位都是厘米（cm）。属性变量是4个，样本数150.

v1，v2，v3，v4是属性变量。v5是原分类观察变量。
每一类。前40个用来设计，后 10个用于检验，因此令外定义变量V6取值和V5相同，但在每组后十个v6值缺失。用于记录预测值，和v5比较后判别分类效果。看下图
![[Pasted image 20240823161554.png]]

基本判别分析用SPSS实现，简便快捷。

打开数据文件或新建数据文件
点击菜单，分析→分类→判别分析，进入判别分析方法框设置
选择属性变量V1-V4进入自变量列表框
选择V6进入分组变量，并定义范围

设置统计量按钮：若要输出Fisher典型判别函数则勾选未标准化复选框。
若要输出每一类Bayes判别函数则勾选Fisher框。SPSS输出的这个函数是在假设总体是正态总体且方差相同的条件下的等效的判别函数，是一个线性函数，不是后验概率的计算公式。
本例中有两个典型判别函数通过了显著性检验
右图是每一类的基于Bayes理论线性判别函数。
![[Pasted image 20240823162155.png]]
![[Pasted image 20240823162208.png]]

典型函数的重要性是和特征值的贡献率有关。
下表说明第一个函数的贡献率已经是99.3%，而第二个只有0.7%。这两个典型判别函数并不是平等的。但两个都通过了显著性检验。同时给出的各类质心得分。对于一个未知样本，计算其判别得分到各类质心的距离来预测其类别
![[Pasted image 20240823162223.png]]
![[Pasted image 20240823162230.png]]

该表给出了三个线性分类函数的系数。把每个观测点带入三个函数，就可以得到分别代表三类的三个值，哪个值最大，该点就属于相应的那一类，称之为模型预测值。当然，我们一开始就知道这些训练数据的类别取值，即训练样本的观测值。比较预测值和观察值，找到错分的样本。SPSS用**‘标注。这里84号样本被错分。 91,92,93测试样本都被正确分到第二类。
![[Pasted image 20240824020551.png]]
![[Pasted image 20240824020609.png]]

继续，设置保存按钮：
若要保存典型函数的敢值，则勾选判别得分。
若要观察模型的预测分类值，勾选预测组成员。属于各类的后验概率在组成员概率中给出。
所有数值追加在当前数据表之后。比较V5和预测组成员的取值，可以看到每组未分类的10个测试点都被正确分类。
![[Pasted image 20240824020733.png]]

继续，设置分类按钮：
勾选摘要表，输出判别分析的准确率判别得分。
勾选合并组：得到典型函数得分散点图。
勾选输出个案结果，可看到模型预测值，找到错分的个案。
![[Pasted image 20240824020828.png]]
![[Pasted image 20240824020859.png]]

Matlab判别分析命令CLASSIFY

两种Af和Apf已由生物学家W.L.Grogna和W.W.Wirth于1981年根据它们的触角长和翼长加以区分，下面是9只Af和6只Apf的触角长和翼长数据

Apf = [1.14, 1.78; 1.18, 1.96; 1.20, 1.86; 1.26, 2.00; 1.28, 2.00; 1.30, 1.96];

6行两列

Af =[1.24, 1.72; 1.36, 1.74; 1.38, 1.64; 1.38, 1.82; 1.38, 1.90; 1.40, 1.70; 1.48, 1.82; 1.54, 1.82; 1.56, 2.08];

9行两列
给定触角长和翼长分别为（1.24，1.80），（1.28，1.84），（1.40，2.04）三个标本判别他们的类别

MATLAB统计工具箱提供的classify函数，可用来对未知类别的样品进行距离判别和先验分布为正态分布的Bayes判别。

Training = [Apf; Af]  %训练样本的属性变量值 
X = [1.24, 1.8; 1.28, 1.84; 1.4, 2.04] %待判样本
Group = [ones（6, 1) * 1; ones(9,1) * 2] %前6个样本第一类，后9个第二类
[class, err] = Classify(x, Training, Group)  %距离判别
[class, err] = classify（x, training，Group，'linear'）%线性判别函数
[class, err] = classify(x, training, Group, 'quadratic'）%二次判别函数

命令格式：

[class, err] = classify(sample, training, group, type, prior)

Sample：待分样本属性矩阵
Training：训练样本属性矩阵，同类放一起
Group：与训练样本相对应的分类变量值
Type：可指定判别函数的类型
Prior：制定各类样本的先验概率
Class：输出待判样本的类别敢值
Error：误判概率的估计值