探索数据结构：图(二)之图的遍历，Kruskal与Prim算法

✨✨ 欢迎大家来到贝蒂大讲堂✨✨

🎈🎈养成好习惯，先赞后看哦~🎈🎈

所属专栏：数据结构与算法
贝蒂的主页：Betty’s blog

1. 图的遍历

图的遍历方式一般分为两种：深度优先遍历与广度优先遍历。

1.1 深度优先遍历

1.1.1 算法思想

**深度优先遍历（Depth First Search，DFS）**是一种用于遍历或搜索图的算法，过程类似于树的前序遍历。其基本原理为：从图中的某个顶点出发，沿着一条路径尽可能深地探索，直到无法继续前进时，回溯到上一个顶点，再尝试其他未探索的路径。这个过程不断重复，直到所有顶点都被访问到。

具体步骤为：

首先选择一个起始顶点，并将其标记为已访问。
从起始顶点出发，选择一个未访问过的邻接顶点，继续进行深度优先遍历。
如果当前顶点没有未访问的邻接顶点，则回溯到上一个顶点，继续探索上一个顶点的其他未访问邻接顶点。
重复步骤 2 和 3，直到所有顶点都被访问。

比如我们对下面这幅图进行深度优先遍历：

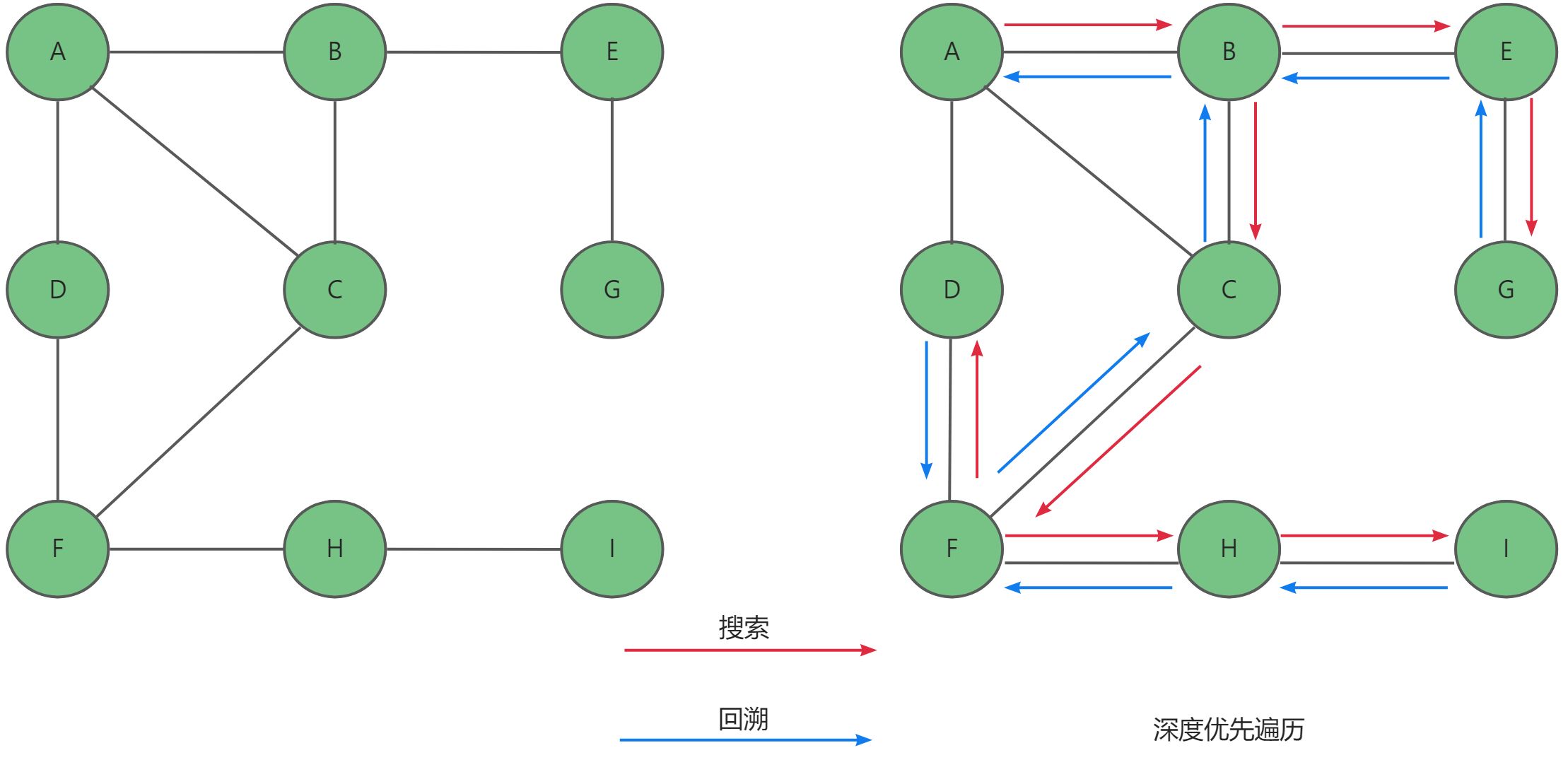
我们首先从A点开始搜索，沿A，B，E，G一直搜索到G然后回溯到B，接着从B开始沿着C，F，D搜索到D，回溯到F，最后沿着H，I搜索到I，搜索完毕。

1.1.2 具体实现

首先我们通过映射关系找到对应下标，然后定义一个判断该点是否已访问的bool数组，最后进行递归访问。在递归访问中，我们首先访问该数据，然后判断该顶点连接的边是否已访问，如果未访问则递归访问，直到所有边都被访问为止。

void _dfs(int srci, vector<bool>& visited)
{
    //先访问
    cout << _vertexs[srci] << " ";
    //标记已访问
    visited[srci] = true;
    for (int i = 0; i < _vertexs.size(); i++)
    {
        //如果存在边且未被遍历
        if (_matrix[srci][i] != MAX_W && visited[i] == false)
        {
            _dfs(i, visited);
        }
    }
}
//深度优先遍历
void dfs(const V& src)
{
    int srci = getVertexsIndex(src);
    //标记已访问的数组
    vector<bool> visited(_vertexs.size(), false);
    _dfs(srci, visited);
    cout << endl;
}

1.2 广度优先遍历

1.2.1 算法思想

**广度优先遍历（Breadth-First Search，BFS）**是一种用于遍历或搜索图的算法，过程类似于树的层序遍历。其基本原理为：从图中的某个顶点出发，先访问该顶点的所有邻接顶点，再依次访问这些邻接顶点的邻接顶点，如此逐步向外扩展，直到所有顶点都被访问到。

具体步骤为：

首先选择一个起始顶点，并将其标记为已访问。
创建一个队列，将起始顶点放入队列中。
从队列中取出一个顶点，访问该顶点，并将其所有未访问过的邻接顶点放入队列中。
重复步骤 3，直到队列为空。

比如我们对下面这幅图进行广度优先遍历：

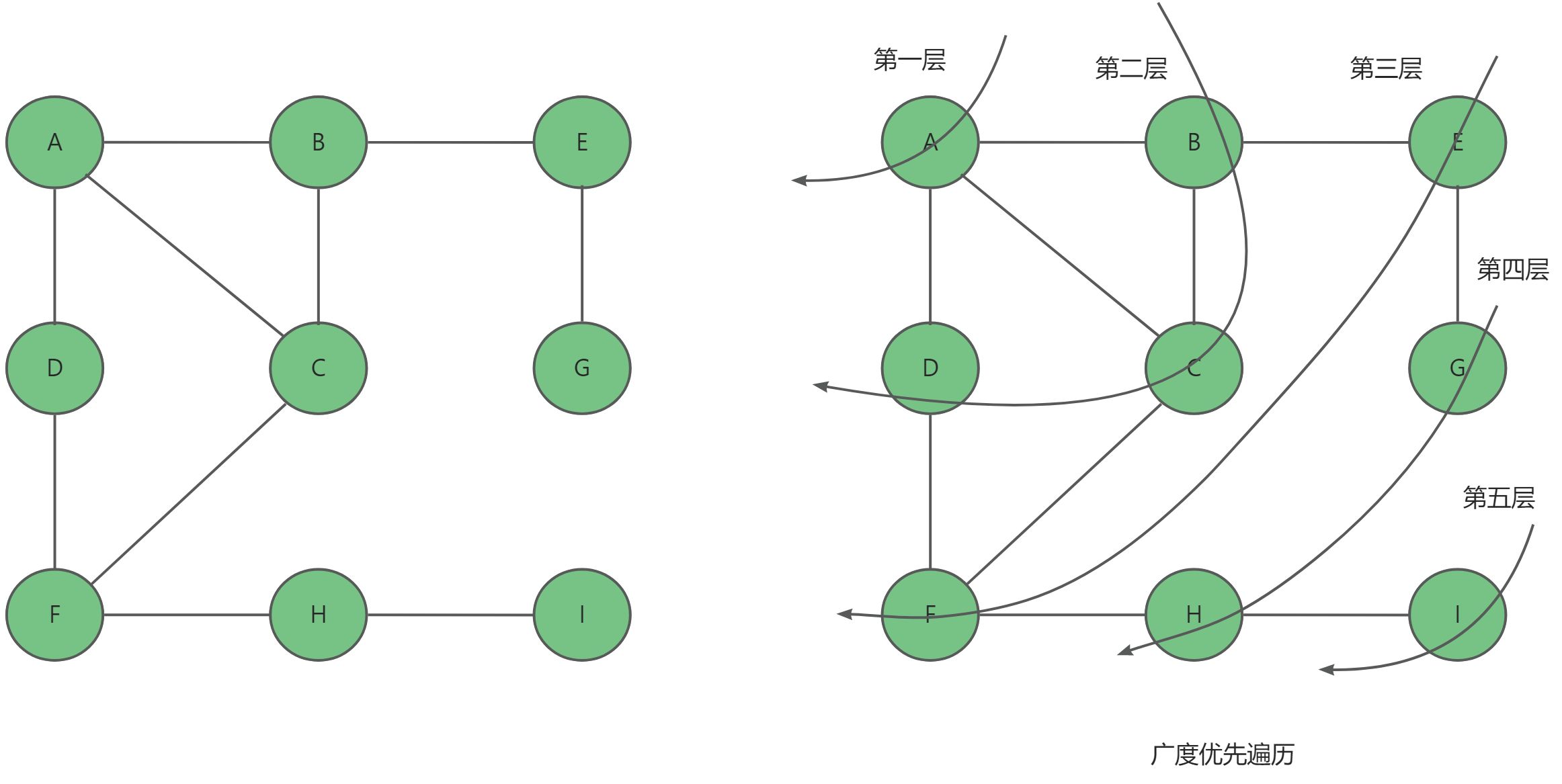
我们首先从A点开始搜索，然后将B，C，D添加到队列，搜索B，C，D过程中再将E，F添加到队列中，接着搜索E，F过程中再将H，G添加到队列，最后搜索完H，G，将I添加到队列，然后搜索完I即搜索完毕。

1.2.2 具体实现

首先我们通过映射关系找到对应下标，然后定义一个判断该点是否已访问的bool数组，将起始顶点对应的下标加入队列。然后访问队列中的元素，访问完的数据我们需要先出队列。最后判断该顶点连接的边是否已访问，如果未访问则继续加入队列，直到所有边都被访问完为止。

//广度优先遍历
void bfs(const V& src)
{
    //获取对应下标
    int srci = getVertexsIndex(src);
    queue<int> q;
    //标记是否被访问的数组
    vector<bool> visited(_vertexs.size(), false);
    q.push(srci);
    visited[srci] = true;
    while (!q.empty())
    {
        int front = q.front();
        q.pop();
        cout << _vertexs[front] << " ";
        for (int i = 0; i < _vertexs.size(); i++)
        {
            //如果存在边，并且没有被访问
            if (_matrix[front][i] != MAX_W && visited[i] == false)
            {
                q.push(i);
                visited[i] = true;
            }
        }
    }
    cout << endl;
}

2. 最小生成树算法

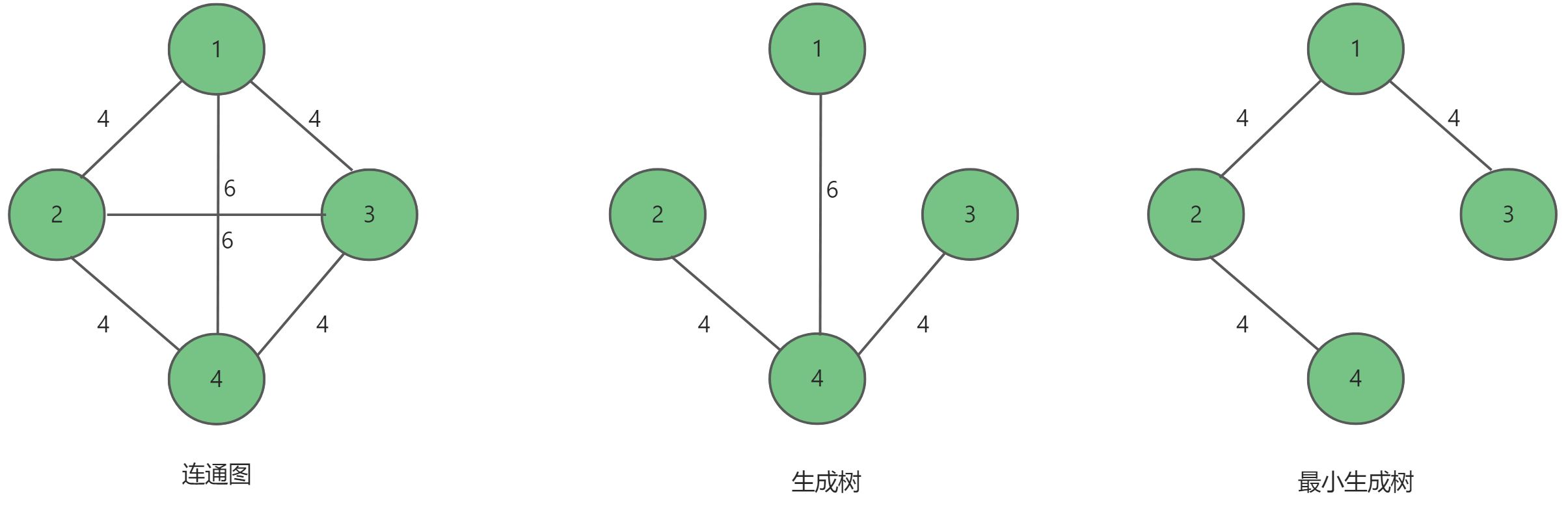
首先我们回忆一下，一个连通图的最小连通子图称为该图的生成树，有 $n$ 个顶点的连通图的生成树有 $n$ 个顶点和 $n - 1$ 条边。最小生成树指的是一个图的生成树中，总权值最小的生成树，并且权值都为正数。

常用的最小生成树算法有两种：Kruskal算法（克鲁斯卡尔算法）和Prim算法（普里姆算法），这两者都采用了贪心的策略。

2.1 Kruskal

2.1.1 算法思想

Kruskal算法是一种用于求解无向加权图最小生成树的算法。该算法的目标是在图中找到一个连通子图，它包含了图中的所有顶点，并且边的权值之和最小。其基本思想是按照边的权值从小到大的顺序依次选择边，在选择边的过程中，避免形成回路。
具体步骤如下：

首先将图中的所有边按照权值从小到大进行排序。
从权值最小的边开始，依次检查每条边。
如果选择这条边不会形成回路，则将其加入最小生成树中。
如果选择这条边会形成回路，则跳过该边，继续检查下一条边。

重复步骤 2，直到最小生成树中包含了图中的所有顶点，或者已经检查完了所有的边。

首先第一步对所有边的权值进行一次排序，然后选出权值最小的边h-g。

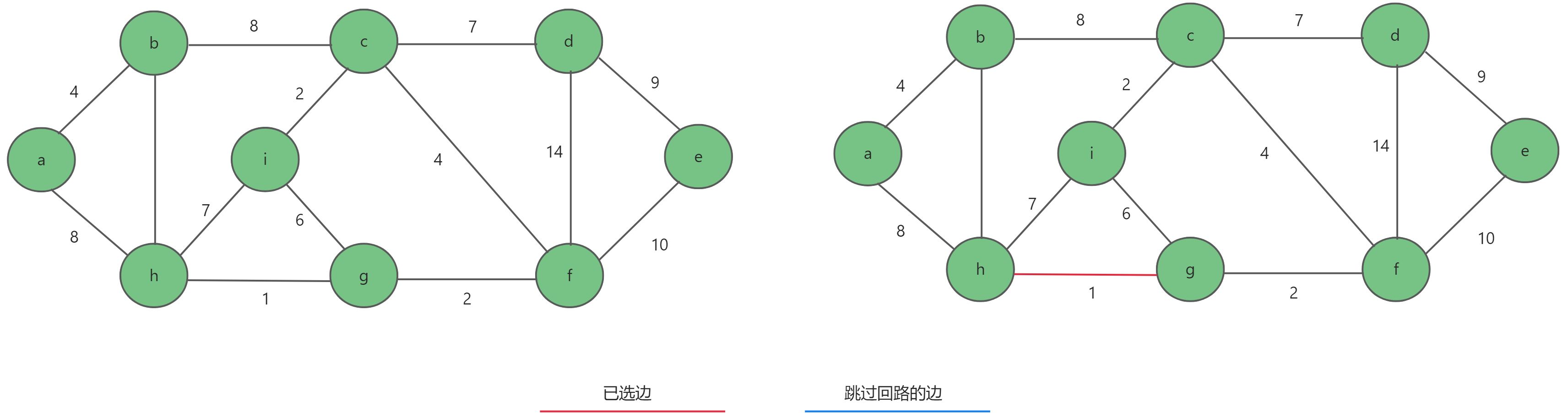
继续选择权值最小的边，分别选择了g-f，c-i，a-b，c-f。然后选择i-g时，形成回路，跳过此边。

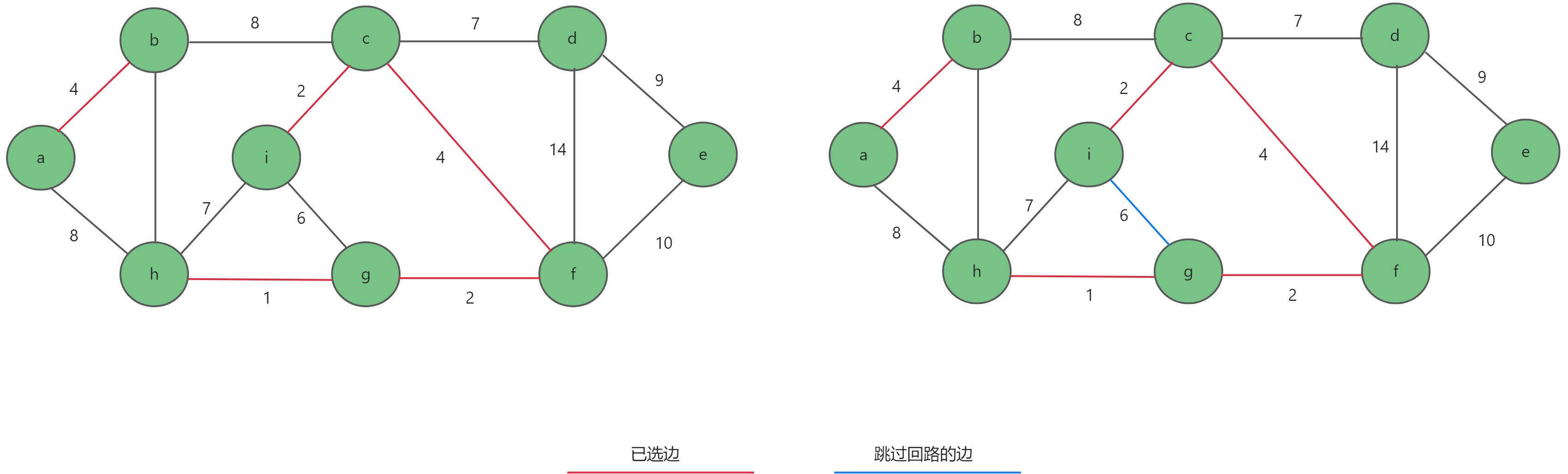
继续选择权值最小的边，选择c-d，再选择h-i形成回路。然后跳过，继续选择a-h，b-c形成回路。

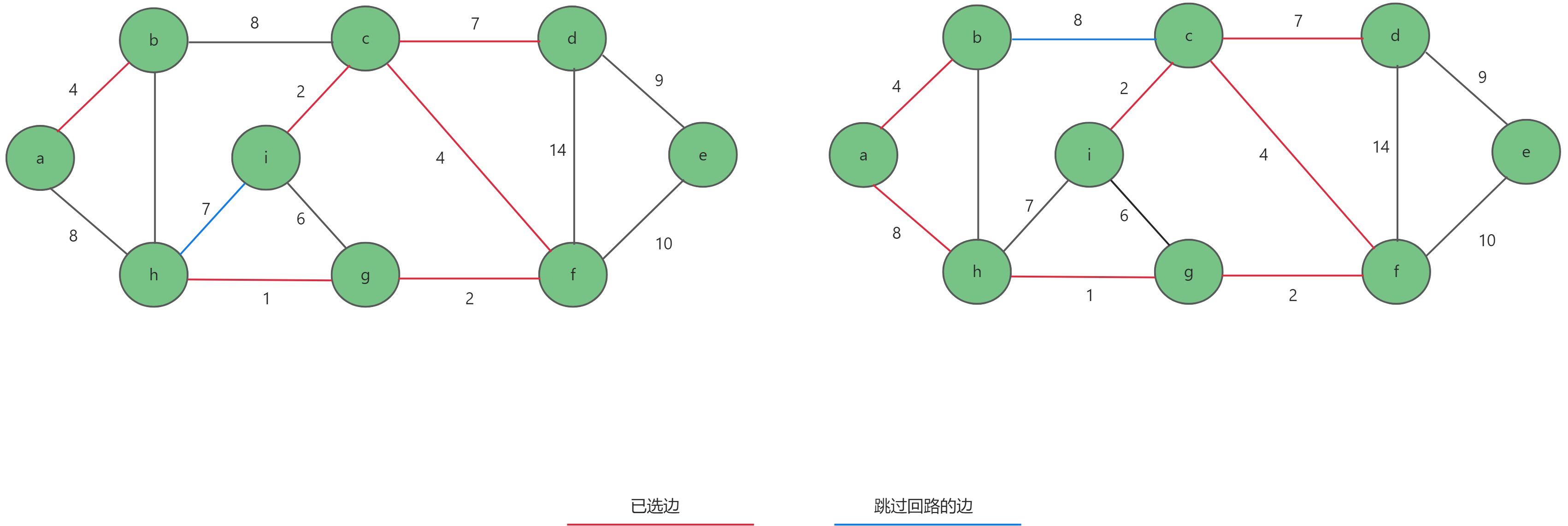
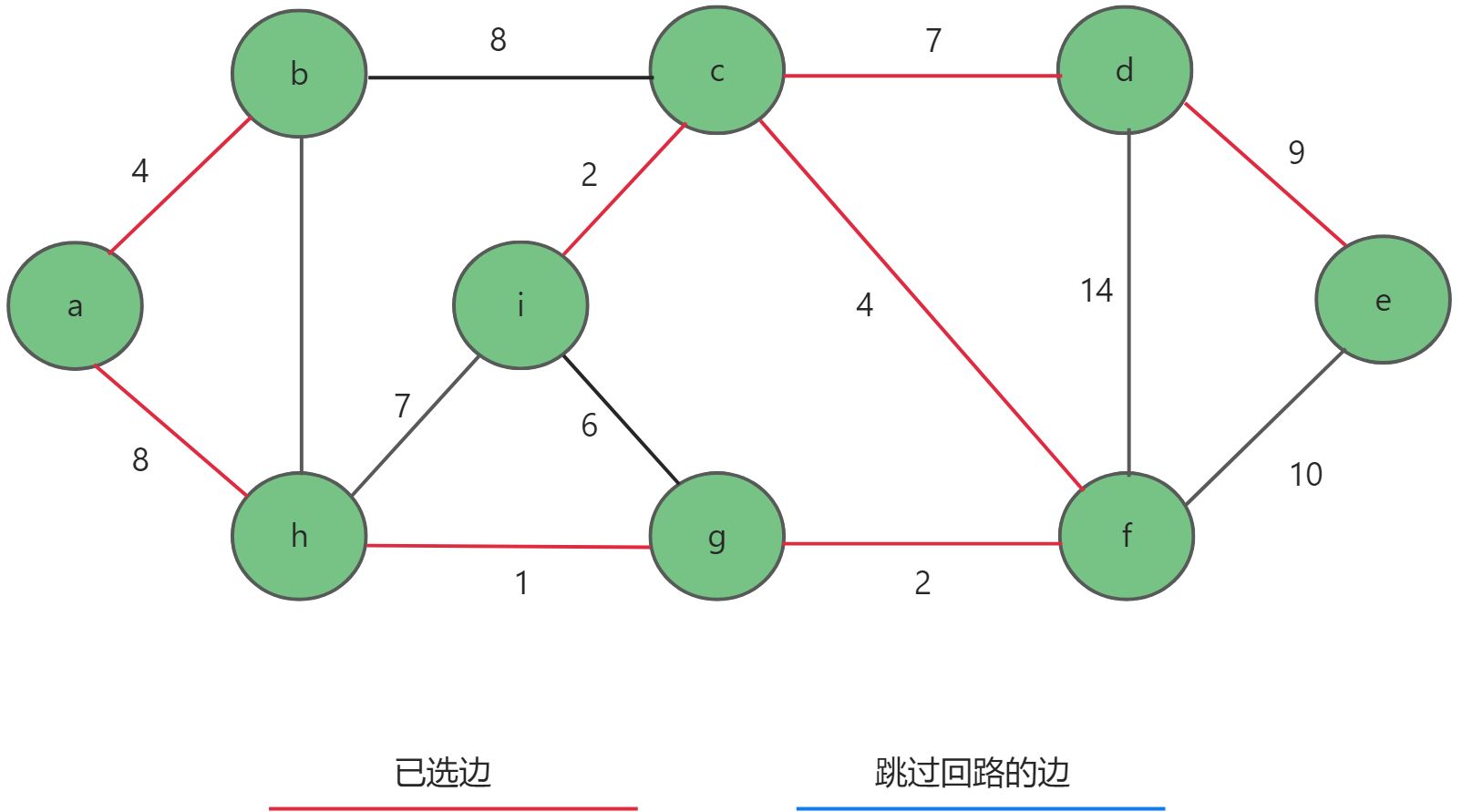
最后选择边d-e，接下来无论选择任何边都会形成回路，并且此时边数恰好比节点数少一，选择完毕。

2.1.2 具体实现

每次选取权值最小的边，我们可以使用优先级队列priority_queue实现。判断是否成环，我们可以利用前面我们实现的并查集UnionFindSet实现。并且值得注意的是：向堆中添加边时，无向图只需要添加一次即可。

struct Edge
{
    int _srci; //源顶点的下标
    int _desti; //目标顶点的下标
    W _weight; //权值
    Edge(int srci, int desti, const W& weight)
        :_srci(srci)
        , _desti(desti)
        , _weight(weight)
    {}
    bool operator > (const Edge& edge) const
    {
        return _weight > edge._weight;
    }
};
//Kruskal算法
W Kruskal(Graph<V, W, MAX_W, Direction>& minTree)
{
    //初始化
    int n = _vertexs.size();
    minTree._vertexs = _vertexs;
    minTree._indexMap = _indexMap;
    minTree._matrix.resize(n, vector<W>(n, MAX_W));
    //小堆
    priority_queue<Edge, vector<Edge>, greater<Edge>> minHeap;
    for (int i = 0; i < n; i++)
    {
        //无向图只需添加一半边
        for (int j = 0; j < i; j++)
        {
            if (_matrix[i][j] != MAX_W)
            {
                minHeap.push(Edge(i, j, _matrix[i][j]));
            }
        }
    }
    UnionFindSet ufs(n);//并查集判断是否成环
    int count = 0;//已选边的数量
    W total = W();//计算选出总权值
    while (!minHeap.empty() && count < n - 1)
    {
        //选最小边
        Edge minEdge = minHeap.top();
        minHeap.pop();
        int srci = minEdge._srci, desti = minEdge._desti;
        W weight = minEdge._weight;
        if (!ufs.inSameSet(srci, desti))
        {
            //添加边
            minTree._matrix[srci][desti] = weight;
            if (Direction == false)
            {
                minTree._matrix[desti][srci] = weight;
            }
            ufs.unionSet(srci, desti);
            //边数++
            count++;
            total += weight;
            cout << "选边: " << _vertexs[srci] << "->" << _vertexs[desti] << ":" << weight << endl;
        }
        else
        {
            cout << "成环: " << _vertexs[srci] << "->" << _vertexs[desti] << ":" << weight << endl;
        }
    }
    //边数与比节点少一
    if (count == n - 1)
    {
        cout << "构成最小生成树" << endl;
        return total;
    }
    else
    {
        cout << "无法构成最小生成树" << endl;
        return W();
    }
}

2.2 Prim

2.2.1 算法思想

Prim算法是一种用于求解无向加权图最小生成树的算法。该算法的目标同样是在图中找到一个连通子图，它包含了图中的所有顶点，并且边的权值之和最小。其基本思想是以一个顶点为起点，逐步向外扩展，每次选择一条连接已加入最小生成树的顶点集和未加入顶点集的权值最小的边。
具体步骤如下：

任选一个顶点作为起始顶点，将其加入最小生成树中。
维护一个集合，记录已加入最小生成树的顶点。初始时，该集合只包含起始顶点。
对于已加入最小生成树的每个顶点，检查其所有邻接边，找到连接已加入顶点集和未加入顶点集的权值最小的边。
将找到的权值最小的边对应的顶点加入最小生成树中，并更新已加入顶点集。
重复步骤 3 和 4，直到最小生成树中包含了图中的所有顶点。

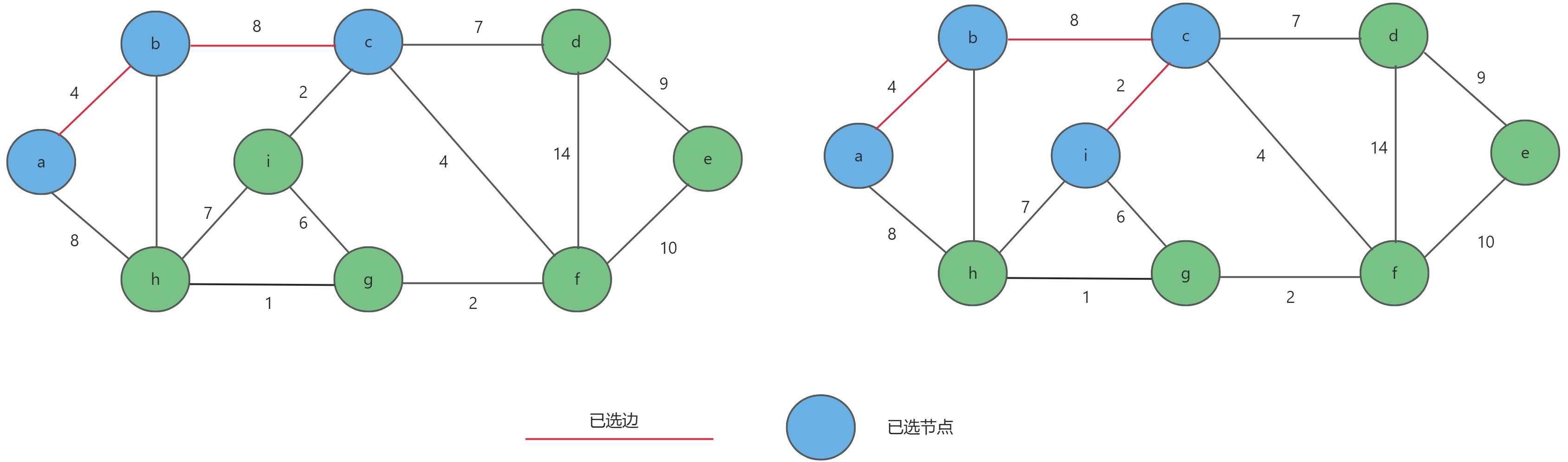
首先从a点开始选择，其中与a点直接相连的边有a-b与a-h，选择权值最小的边a-b加入。

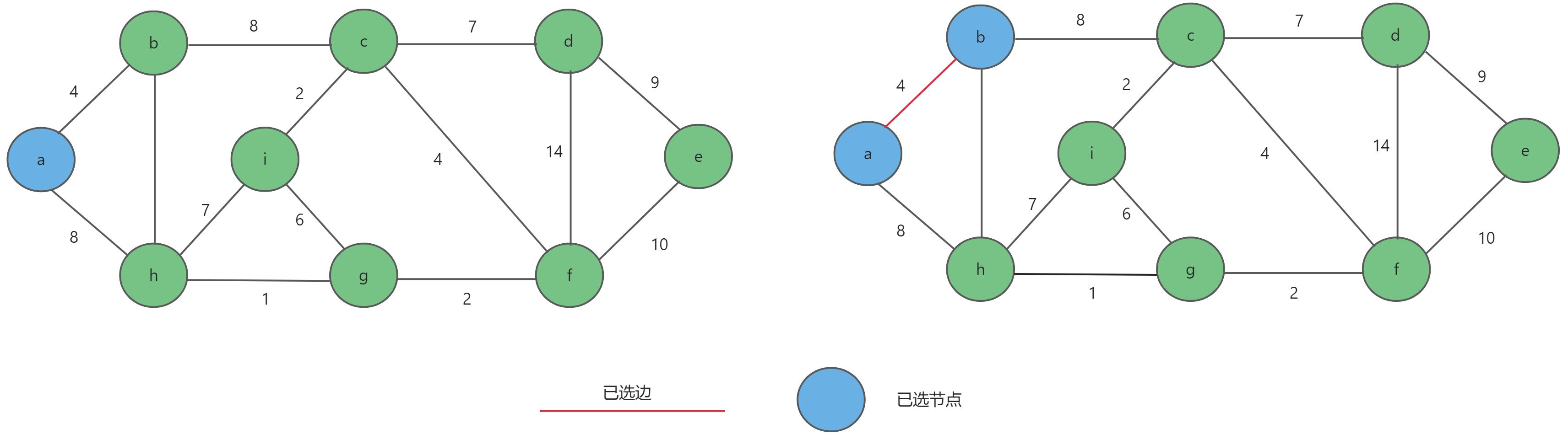
同样以a，b作为起始点选取权值最小的边b-c，同理选出c-i。

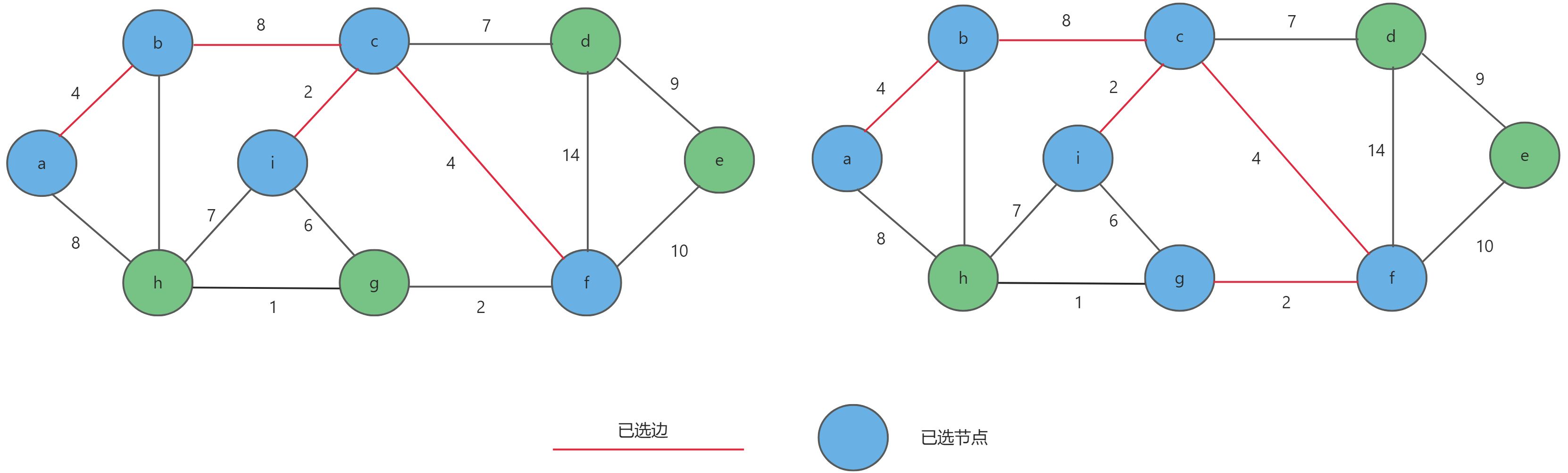
同样以a，b，c，i作为起始点选取权值最小的边c-f，同理选出f-g。

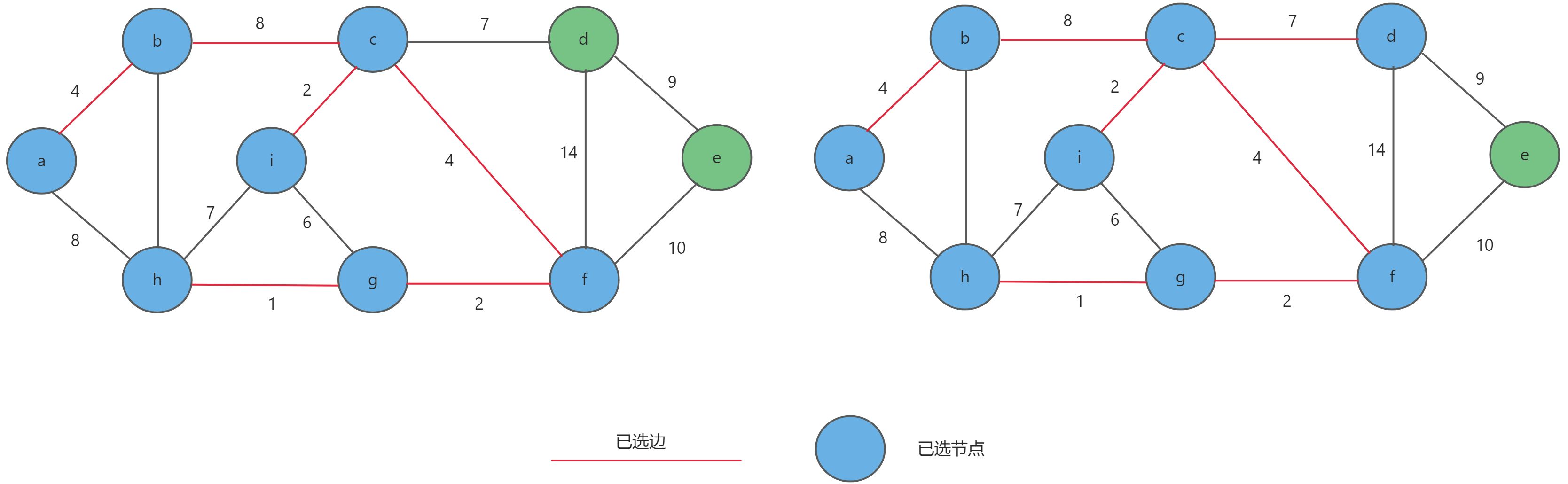
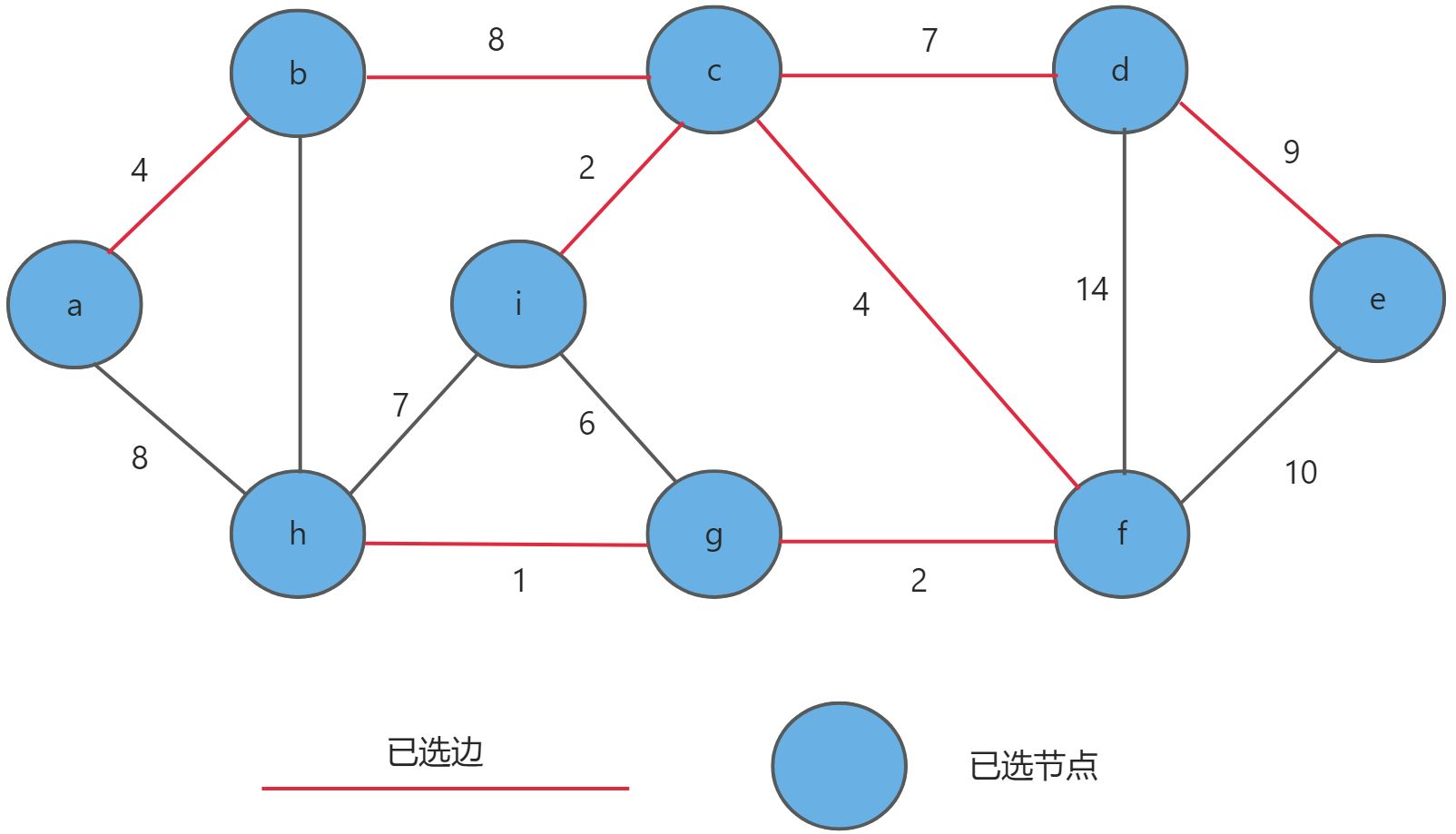
最后再依次g-h，c-d，d-e，选取完毕。

2.2.2 具体实现

为了防止成环，我们采用定义一个bool类似数组

//Prim算法
W Prim(Graph<V, W, MAX_W, Direction>& minTree,const V& start)
{
    //初始化
    int n = _vertexs.size();
    minTree._vertexs = _vertexs;
    minTree._indexMap = _indexMap;
    minTree._matrix.resize(n, vector<W>(n, MAX_W));
    int starti = getVertexsIndex(start);//获取对应下标
    //小堆
    priority_queue<Edge, vector<Edge>, greater<Edge>> minHeap;
    //已访问顶点的集合
    vector<bool> visited(n, false);
    visited[starti] = true;
    for (int i = 0; i < n; i++)
    {
        //将该顶点相连的边全部添加进堆
        if (_matrix[starti][i] != MAX_W)
        {
            minHeap.push(Edge(starti, i, _matrix[starti][i]));
        }
    }
    int count = 0;//已选边的数量
    W total = W();//计算选出总权值
    while (!minHeap.empty() && count < n - 1)
    {
        //选最小边
        Edge minEdge = minHeap.top();
        minHeap.pop();
        int srci = minEdge._srci, desti = minEdge._desti;
        W weight = minEdge._weight;
        //如果该节点没有被添加进集合中
        if (visited[desti] == false)
        {
            for (int i = 0; i < n; i++)
            {
                //将该顶点相连的边全部添加进堆
                if (_matrix[desti][i] != MAX_W && visited[i] == false)
                {
                    minHeap.push(Edge(desti, i, _matrix[desti][i]));
                }
            }
            //添加边
            minTree._matrix[srci][desti] = weight;
            if (Direction == false)
            {
                minTree._matrix[desti][srci] = weight;
            }
            visited[desti] = true;
            //边数++
            count++;
            total += weight;
            cout << "选边: " << _vertexs[srci] << "->" << _vertexs[desti] << ":" << weight << endl;
        }
        else
        {
            cout << "成环: " << _vertexs[srci] << "->" << _vertexs[desti] << ":" << weight << endl;
        }
    }
    //边数与比节点少一
    if (count == n - 1)
    {
        cout << "构成最小生成树" << endl;
        return total;
    }
    else
    {
        cout << "无法构成最小生成树" << endl;
        return W();
    }
}