基于距离度量学习的异常检测：一种通过相关距离度量的异常检测方法

异常通常被定义为数据集中与大多数其他项目非常不同的项目。或者说任何与所有其他记录(或几乎所有其他记录)显著不同的记录,并且与其他记录的差异程度超出正常范围,都可以合理地被认为是异常。

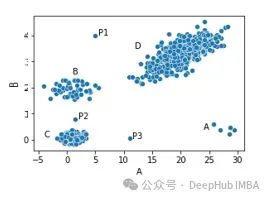
例如上图显示的数据集中,我们有四个簇(A、B、C和D)和三个位于这些簇之外的点:P1、P2和P3可能被视为异常,因为它们每个都远离所有其他点 - 也就是说,它们与大多数其他点有显著差异。

同样,簇A只有五个点。虽然这些点彼此相当接近,但它们远离所有其他点,所以也可能被认为是异常。内点(较大簇内的点)都非常接近大量其他点。例如,簇C中间的任何点都非常接近许多其他点(即与许多其他点非常相似),所以不会被视为异常。

我们可以用许多其他方式来看待异常,实际上许多其他方法也用于异常检测 - 例如基于频繁项集、关联规则、压缩、马尔可夫模型等的异常检测方法。但是事实上,最常见的异常检测算法背后的基本思想,包括kNN、LOF(局部异常因子)、Radius等众多算法，都是使用数据见距离来进行计算的。

这就引出了一个问题:如何量化一条记录与其他记录的差异程度。在异常检测中最常见的一些包括欧几里得距离、曼哈顿距离和Gower距离,以及许多类似的度量。

但在本文中,将一种非常通用且可能未被充分使用的方法,用于计算表格数据中两条记录之间的差异,这对异常检测非常有用,称为距离度量学习 - 以及一种专门应用于异常检测的方法。

距离度量

为了确定一条记录是否1)异常地远离大多数其他记录;2)接近相对较少的记录,我们通常首先计算成对距离:数据集中每对记录之间的距离。这意味着我们需要一种方法来计算任意两条记录之间的距离。

如果我们有一组如下所示的数据,一个大型员工记录表(这里显示了随机子集的四行),我们如何说任意两行有多相似?

欧几里得距离

一种非常常见的方法是使用欧几里得距离。

由于这个数据集只包含两个特征,并且都是数值型的,将数据绘制成散点图是相当直观的。一旦以这种方式绘制,我们自然会想象点之间的欧几里得距离(基于勾股定理)。

但是如果有许多特征，或者其中许多是分类的;以及列之间存在关联,行之间的欧几里得距离虽然仍然有效并且经常有用,但可能感觉不那么自然。

欧几里得距离的一个问题是它们实际上是为数值数据设计的,但大多数现实世界的数据,比如员工记录包含数值和分类特征。分类值可以用数字编码(例如使用One-Hot、Ordinal或其他编码方法),然后可以计算欧几里得距离(以及其他数值距离度量)。但这并不是最好的方法，因为每种数值编码方法对计算的距离都有自己的影响。

让我们假设使用one-hot编码对这些特征进行编码。要计算行之间的欧几里得距离,我们还必须缩放数值特征,将所有特征放在相同的尺度上。这可以通过多种方式完成,包括标准化(将值转换为z值,基于该值距离该列平均值的标准差数)或最小-最大缩放。

一旦数据被数值编码和缩放,我们就可以计算每对行之间的欧几里得距离。

Gower距离

考虑到我们有一些分类特征,所以可以使用为混合数据设计的方法,如Gower距离。这种方法比较任意两行时,逐列取差异并求和。对于严格的数值数据,它等同于曼哈顿距离。

对于分类列,使用Gower距离时,通常使用Ordinal编码,因为我们只关心是否完全匹配。分类列中两个值的差异要么是0.0,要么是1.0。在上面的员工表中,Smith和Jones的部门距离为1.0(1.0总是用于不同的值:在这种情况下是"工程"和"销售"),办公室距离为0.0(0.0总是用于两行具有相同的值:在这种情况下是"多伦多")。

要比较数值字段,与欧几里得距离和大多数距离度量一样,首先需要对它们进行缩放，这样所有数值字段可以被平等对待。有许多方法可以做到这一点,我们在这里使用min-max缩放,这将所有值放在0.0到1.0之间的尺度上。然后我们可能会得到如下表格:

Smith和Jones之间的差异(使用Gower距离)将是:abs(0.90 - 0.20) + abs(0.93 - 0.34) + abs(0.74 - 0.78) + 1.0 + abs(0.88 - 0.77) + abs(0.54 - 0.49) + 0.0 + abs(0.32 - 0.38)。

也就是说,跳过ID和姓氏,计算每个数值字段的绝对差异,对每个分类字段取0.0或1.0。

这可能是合理的,但确实存在一些问题。比如说一个可能是分类字段的权重大于数值字段:它们通常会有1.0的差异,而数值值往往会有较小的差异。例如,Smith和Jones之间的年龄差异相当大,但只会有abs(0.93-0.34)或0.59的差异小于部门对行之间总差异贡献的1.0)，这就引出了距离度量在处理混合数据时存在一个的问题，无法确定各个特征的度量权重。

另外所有分类特征彼此同等相关;所有数值特征彼此同等相关,即使其中一些高度相关,或者可能应该承担更多或更少的权重，这也是权重的问题。

所以欧几里得距离或Gower距离(以及其他度量如曼哈顿距离、堪培拉距离等)等距离度量在许多情况下可能是适当的距离度量,并且通常是异常检测的极好选择。但它们可能并不总是适合所有项目的理想选择。

高维空间中的物理距离

再次回到欧几里得距离,我们会将每条记录视为高维空间中的点,并计算这个空间中这些点之间的距离。曼哈顿距离和Gower距离有点不同,但工作方式非常相似。

我们这个表只包括数值特征:服务年限、年龄、薪水、假期天数、病假天数和上次奖金。这是六个特征,所以每一行可以被视为6维空间中的一个点,它们之间的距离使用勾股定理计算是合理的,但肯定不是距离的唯一方式。使用的距离度量可能会对分配的异常分数产生实质性的影响。例如,欧几里得距离可能比曼哈顿距离更强调少数具有非常不同值的特征。

欧几里得距离和曼哈顿距离的示例

我们看看6维数据的两种不同情况(也显示ID和姓氏列以供参考)。

第一个例子是两名员工Greene和Thomas,其中大多数值相似,但服务年限非常不同:

第二个例子是另外两名员工Ford和Lee,大多数值都有中度差异,但没有一个非常不同:

这两对行中哪一对最相似?使用曼哈顿距离,Greene和Thomas最相似(距离为0.59,相比之下为0.60)。使用欧几里得距离,Ford和Lee最相似(距离为0.27,相比之下为0.50)。

所以使用那种距离来进行度量呢？这不一定是一个问题,但它确实突出表明有很多方法可以计算出不同的距离。

特别是欧几里得距离意味着我们将数据视为高维空间中的点,并取它们之间相当于物理距离的东西。欧几里得距离需要取年龄的平方、薪水的平方等 - 这缺乏任何直观理论基础，因为年龄平方到底意味着什么并不清楚。虽然它可以很好地工作,但这并没有可解释性。所以这是一种不考虑数据本身的通用方法。

距离度量学习

距离度量学习提供了另一种思考如何确定两条记录有多相似的问题的方法。它不首先定义一个距离度量然后将其应用于手头的数据,而是试图从数据本身学习记录之间的相似程度。

它还解决了欧几里得距离、曼哈顿距离和大多数其他距离度量的一个限制:所有特征都被平等对待,无论这是否最合适。

距离度量学习想法是:某些特征比其他特征更相关,某些特征也会彼此相关(在某些情况下,一组特征甚至可能是冗余的,或几乎是冗余的)。简单地平等对待每个特征不一定是识别数据集中最异常记录的最佳方法。距离度量学习本身是一个重要领域,我门这里只介绍它如何应用于异常检测的一种方法。

下面我们将介绍基于随机森林的距离度量学习在异常检测中的应用。

我们假设:有一个预测某个目标的随机森林，还有一个可以通过随机森林传递的数据表(例如员工数据,但任何表格数据都可以)，然后我们想计算每对行之间的距离进行计算。

并且暂时假设有一个质量良好、训练充分且健壮的随机森林模型。这个随机森林模型被训练为二元分类器,所以可以为数据中的每条记录产生被预测为正类的概率。

通过随机森林传递的两条记录可能有非常相似的概率,比如说0.615和0.619。这些非常接近,所以我们可以暂时说这两条记录彼此相似（但不肯定），因为它们实际上可能在随机森林内的许多决策树中遵循完全不同的决策路径,恰好平均出相似的预测，所以它们可能出于不同的原因收到相似的预测,并且可能根本不相似。

而最相关的是记录应该是通过决策树的决策路径来判断。如果两条记录在大多数树中走相同的路径(因此在相同的叶节点结束),那么我们可以说它们是相似的(至少在随机森林这个算法中)。如果它们大部分时间在不同的叶节点结束,我们可以说它们是不同的。

基于以上的理论，我们可以以一种合理的方式确定任何两条记录有多相似。

创建随机森林

但是上面我们说了，需要假设一个质量良好、训练充分且健壮的随机森林模型。创建这样一个随机森林的一种方法是构建一个学习区分这些数据与虚假数据的随机森林。

如果我们能创建这样一组虚假数据,就可以训练一个随机森林分类器来区分这两种类型的数据。

有许多方法可以创建这里使用的合成数据,例如,doping (我们以前介绍过)。但是我们介绍另一种很有效的方法。这种方法非常简单，并且可能并不是十分有效，但是它十分适合我们这个文章。

我们一次生成一行合成数据,对每一行,一次生成一个特征。

生成的值,如果特征是分类的,我们从真实数据中选择一个值,概率与真实数据中的分布成比例。例如,如果真实数据包含一个颜色列,其中包含450行红色,650行蓝色,110行绿色和385行黄色,那么作为分数,这些是:红色:0.28,蓝色:0.41,绿色:0.07,黄色:0.24。将用类似比例在合成数据的这一列中创建一组新值。

如果特征是数值型的,计算该特征在真实数据中的平均值和标准差,并从具有这些参数的正态分布中选择一组随机值。当然也可以考虑其他许多方法来做这个，我们这里只是为了简单。

这生成合成数据中每一行都由完全现实的值组成(每一行在分类列中可能包含罕见的值,在数值列中可能包含罕见或极端的值 - 但它们都是合理现实的值)。

但是特征之间的正常关系没有得到保留，也就是说:由于每个列值是独立生成的，特征之间的关系是没有的。例如,如果创建合成数据来模仿上面的员工表,我们可能会创建年龄为23岁和服务年限为38年的假记录。这两个值本身都是真实的,但组合是非常荒谬的,或者说是真实数据中看不到的组合 - 这样就可以与真实数据区分开来。

我们可以使用以下代码(用python)创建数值字段的合成数据:

 real_df['Real'] =True
 synth_df=pd.DataFrame() 
 forcol_nameinreal_df.columns:
     mean=real_df[col_name].mean()
     stddev=real_df[col_name].std()
     synth_df[col_name] =np.random.normal(
        loc=mean, scale=stddev, size=len(real_df))
 synth_df['Real'] =False
 train_df=pd.concat([real_df, synth_df])

我们假设real_df包含真实数据。然后创建一个名为synth_df的第二个df,将两者合并到train_df中,可以用来训练随机森林以区分两者。

类似地可以创建分类数据:

 forcol_nameinreal_df.columns:    
     vc=real_df[col_name].value_counts(normalize=True)
     synth_df[col_name] =np.random.choice(a=vc.keys().tolist(), 
                                           size=len(real_df),
                                           replace=True, 
                                           p=vc.values.tolist())

这只是生成数据的一种方式,也可以调整这个过程,增加更不寻常的单个值,或限制特征之间不寻常的关系。

创建了这些数据,我们就可以训练一个随机森林来学习区分真实数据和虚假数据。一旦完成,我们实际上还可以执行另一种形式的异常检测。

使用随机森林测量异常程度

上面我们已经说了，如果两条记录倾向于在几乎完全不同的叶节点结束,它们可以被认为是不同的,至少在这个意义上是这样。

对于每对记录,可以计算它们在随机森林内的树中结束在相同叶节点和不同叶节点的数量（因为我们是随进森林，有很多树）。但是也可以使用一种更简单的方法，对于通过随机森林的每条记录,对于每棵树,我们可以看到叶节点是什么。还可以看到有多少训练数据记录结束在该节点。

如果在大多数树中，一条记录结束于与极少数其他记录相同的叶节点，则可以认为它是异常的。

详细解释如下:如果随机森林是准确的,它可以很好地区分真实和虚假记录。因此当通过随机森林传递真实记录时,它可能会结束在与真实数据相关的叶节点中。如果它是一个正常的真实记录,它将遵循一个常见的路径,被许多其他真实记录使用。在路径的每一步,决策树中的节点都会在一个特征上分裂 - 一个有效分离真实和合成数据的特征和分裂点。一个典型的记录将具有与常见真实数据相关的值,因此将在每个分裂点遵循与真实数据相关的路径。

如果随机森林只包含少量树,每条记录结束的叶节点的大小可能相当任意。当记录一致地结束在对其树而言不寻常的叶节点中时,该记录可以合理地被认为是异常的。

示例

为了演示这个想法,我们将创建一个简单的距离度量学习检测器。

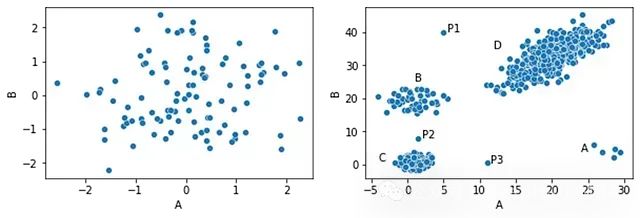
但首先创建几个测试数据集。这些都是具有两个特征的数值数据集。如前所述,这不如具有许多特征和许多分类特征的数据现实,但它对于演示目的很有用 - 它易于绘制和理解。

第一个测试集是单个数据簇:

 importnumpyasnp
 importpandasaspd
 
 defcreate_simple_testdata():
     np.random.seed(0)
     a_data=np.random.normal(size=100)
     b_data=np.random.normal(size=100)
     df=pd.DataFrame({"A": a_data, "B": b_data})
     returndf

第二个创建了文章开头所示的数据集,有四个簇和三个在这些簇之外的点。

 defcreate_four_clusters_test_data():  
     np.random.seed(0)  
   
     a_data=np.random.normal(loc=25.0, scale=2.0, size=5)   
     b_data=np.random.normal(loc=4.0, scale=2.0, size=5)  
     df0=pd.DataFrame({"A": a_data, "B": b_data})  
   
     a_data=np.random.normal(loc=1.0, scale=2.0, size=50)   
     b_data=np.random.normal(loc=19.0, scale=2.0, size=50)  
     df1=pd.DataFrame({"A": a_data, "B": b_data})  
   
     a_data=np.random.normal(loc=1.0, scale=1.0, size=200)   
     b_data=np.random.normal(loc=1.0, scale=1.0, size=200)  
     df2=pd.DataFrame({"A": a_data, "B": b_data})  
   
     a_data=np.random.normal(loc=20.0, scale=3.0, size=500)   
     b_data=np.random.normal(loc=13.0, scale=3.0, size=500) +a_data  
     df3=pd.DataFrame({"A": a_data, "B": b_data})  
   
     outliers= [[5.0, 40],   
                 [1.5, 8.0],  
                 [11.0, 0.5]]  
     df4=pd.DataFrame(outliers, columns=['A', 'B'])  
   
     df=pd.concat([df0, df1, df2, df3, df4])  
     df=df.reset_index(drop=True)  
     returndf

这两个数据集如下所示:

然后我们创见一个基于距离度量学习的简单异常检测器。这个检测器的fit_predict()方法传入一个df(我们在其中识别任何异常)。fit_predict()方法生成一个合成数据集,训练随机森林,将每条记录通过随机森林,确定每条记录结束在哪个节点,并确定这些节点有多常见。

 fromsklearn.ensembleimportRandomForestClassifier  
 fromcollectionsimportCounter  
 fromsklearn.preprocessingimportRobustScaler  
   
 classDMLOutlierDetection:  
     def__init__(self):  
         pass  
   
     deffit_predict(self, df):  
         real_df=df.copy()  
         real_df['Real'] =True  
   
         # 生成与真实数据相似的合成数据  
         # 为简单起见,这里只涵盖数值情况    
         synth_df=pd.DataFrame()   
         forcol_nameindf.columns:  
             mean=df[col_name].mean()  
             stddev=df[col_name].std()  
             synth_df[col_name] =np.random.normal(loc=mean,   
                scale=stddev, size=len(df))  
         synth_df['Real'] =False  
   
         train_df=pd.concat([real_df, synth_df])  
   
         clf=RandomForestClassifier(max_depth=5)  
         clf.fit(train_df.drop(columns=['Real']), train_df['Real'])  
   
         # 获取每条记录结束的叶节点   
         r=clf.apply(df)   
   
         # 将所有记录的分数初始化为0  
         scores= [0]*len(df)   
   
         # 遍历随机森林中的每棵树  
         fortree_idxinrange(len(r[0])):   
             # 获取每个叶节点的计数  
             c=Counter(r[:, tree_idx])   
               
             # 遍历每条记录并根据其结束节点的频率更新其分数   
             forrecord_idxinrange(len(df)):   
                 node_idx=r[record_idx, tree_idx]  
                 node_count=c[node_idx]  
                 scores[record_idx] +=len(df) -node_count  
   
         returnscores  
   
 df=create_four_clusters_test_data()  
 df=pd.DataFrame(RobustScaler().fit_transform(df), columns=df.columns)  
 clf=DMLOutlierDetection()  
 df['Scores'] =clf.fit_predict(df)

这个代码示例只在create_four_clusters_test_data()创建的数据上运行,但也可以用create_simple_testdata()的数据调用。

结果可以用如下代码可视化:

 importmatplotlib.pyplotasplt  
 importseabornassns  
   
 sns.scatterplot(x=df["A"], y=df['B'], hue=df['Scores'])  
 plt.show()

两个测试数据集的结果如下所示,绘制原始数据,但将色调设置为其异常分数(由上面的代码放置在’Scores’列中)。

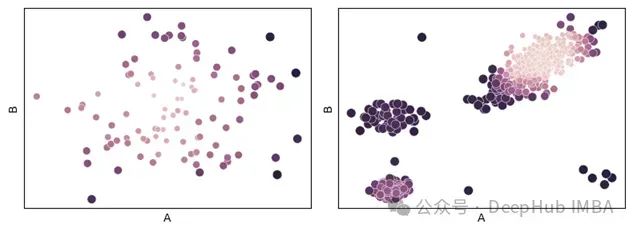
在左侧的数据集中,只有一个簇,最外层的点获得最高分数,这是符合预期的。在右侧的数据集中,有四个簇,最高的异常分数分配给了簇外的三个点、较小的簇,以及最大簇边缘的点。这是相当合理的（因为我们不是聚类，而是检测异常）,尽管其他检测器可能会对这些进行不同的评分,而且可能也相当合理。

总结

距离度量学习可以用于异常检测之外的许多目的,即使在异常检测中,也可以以多种方式使用。比如说可以使用如上所述的随机森林来计算数据集中的成对距离传递给另一个算法。例如,DBSCAN提供了一个"precomputed"选项,允许传递预先计算的成对距离矩阵;然后可以使用DBSCAN(或类似的聚类方法,如HDBSCAN)进行几种可能的基于聚类的异常检测算法。

或者以更直接的方式使用，因为这本身就是一种出色的异常检测方法。在许多情况下,它可能比基于欧几里得、曼哈顿、Gower或其他此类距离度量的方法更有利于检测异常。它还可以为检测器集成提供多样性,即使在这些方法也能很好地工作。

但是距离度量学习不会适用于每个项目,即使在适用的情况下,可能(如同任何检测器一样)在与其他检测器结合使用时表现最佳。但是距离度量学习可以是一种非常有效的异常检测技术,尽管它受到的关注比其他方法少。

https://avoid.overfit.cn/post/81746cc2ef314702a838c2aaa9d57b6b

W Brett Kennedy